数学2.4 圆周角教课ppt课件

这是一份数学2.4 圆周角教课ppt课件，共34页。PPT课件主要包含了教学目标，复习引入，情境引入，知识精讲，圆的内接四边形的概念，圆内接四边形的性质，确定圆的条件，圆内接四边形的判定等内容，欢迎下载使用。

理解圆的内接四边形、四边形的外接圆的概念
掌握并熟练运用圆内接四边形的性质
掌握圆内接四边形的判定，初步认识辅助圆模型
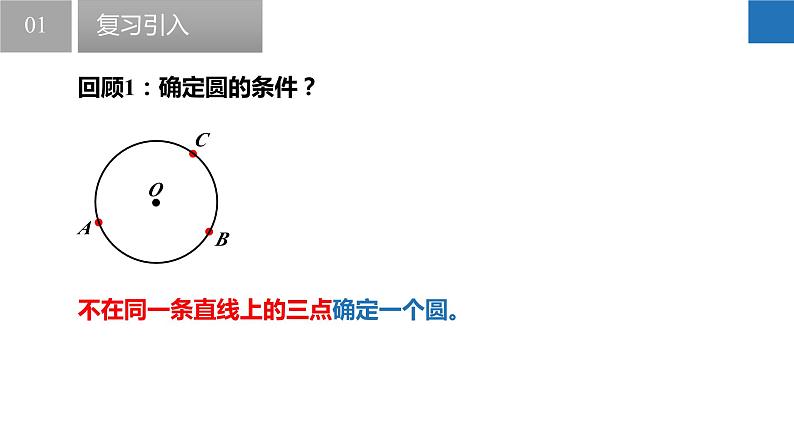
回顾1：确定圆的条件？
不在同一条直线上的三点确定一个圆。
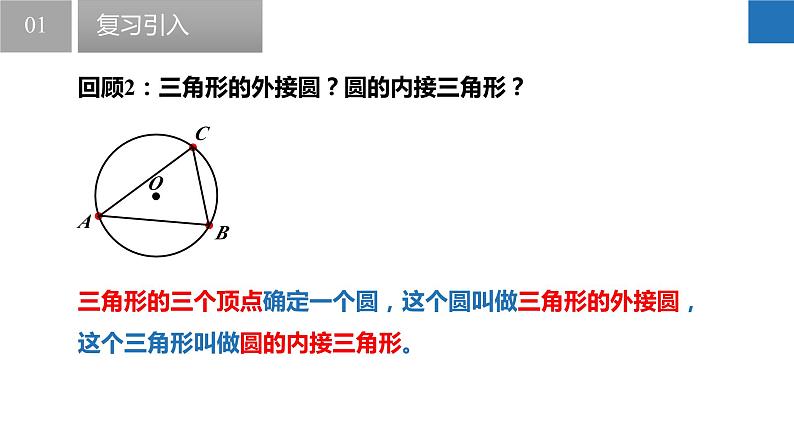
回顾2：三角形的外接圆？圆的内接三角形？
三角形的三个顶点确定一个圆，这个圆叫做三角形的外接圆，这个三角形叫做圆的内接三角形。
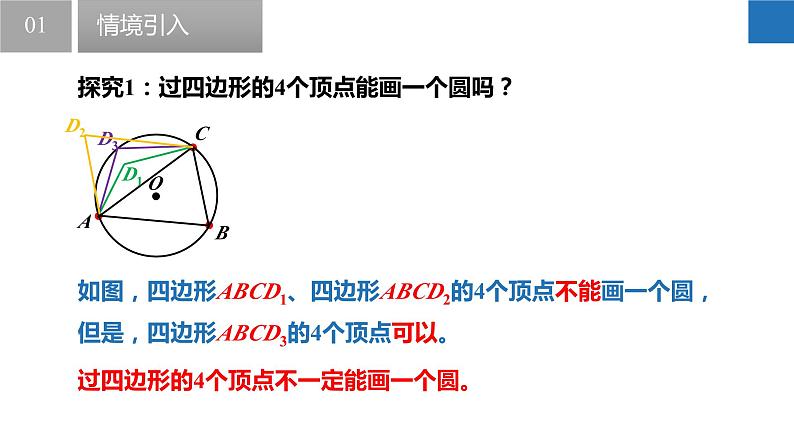
探究1：过四边形的4个顶点能画一个圆吗？
过四边形的4个顶点不一定能画一个圆。
如图，四边形ABCD1、四边形ABCD2的4个顶点不能画一个圆，但是，四边形ABCD3的4个顶点可以。
一个四边形的4个顶点都在同一个圆上，这个四边形叫做圆的内接四边形，这个圆叫做四边形的外接圆。
【思考1-1】如下图，在⨀O的内接四边形ABCD中，BD是⨀O的直径，问：∠A与∠C、∠ABC与∠ADC有怎样的数量关系?
∵BD是⨀O的直径，∴∠A=90°，∠C=90°，∴∠A+∠C=180°。
又∵四边形内角和是360°，∴∠ABC+∠ADC=180°。
【总结】在此情况下，圆内接四边形的对角互补。
【思考1-2】如下图，圆心O不在⨀O的内接四边形ABCD的对角线上，上述结论是否仍然成立?
作直径DE，连接AE、CE，∵BD是⨀O的直径，∴∠DAE+DCE=90°+90°=180°，
【总结】圆内接四边形的对角互补。
【思考1-3】还有其他证明“圆内接四边形的对角互补”的方法吗？【提示：从新学的圆周角的知识点入手】
同理：∠B+∠D=180°。
性质1：圆内接四边形的对角互补。
eg：∠A+∠C=180°，∠B+∠D=180°。
【思考2-1】如下图，四边形ABCD是⨀O的内接四边形，问 ：∠C与∠BOD有怎样的数量关系?
∵四边形ABCD是⨀O的内接四边形，∴∠A+∠C=180°，
【思考2-2】如下图，B、C、D是⨀O上的三个点，已知∠C=105°，求∠BOD的度数?
设点A是优弧BD上一点（不与B、D重合），连接AB、AD，
根据题意可得：∠A+∠C=180°，∵∠C=105°，∴∠A=75°，∴∠BOD=2∠A=150°。
【总结】需要利用辅助线构造圆的内接四边形。
【思考3】如下图，四边形ABCD是⨀O的内接四边形，∠BAE是∠BAD的外角，问 ：∠C与∠BAE有怎样的数量关系?
∵四边形ABCD是⨀O的内接四边形，∴∠BAD+∠C=180°，
又∵∠BAD+∠BAE=180°，∴∠C=∠BAE。
【总结】圆内接四边形的任意一个外角等于它相邻的内角的对角。
性质2：圆内接四边形的任意一个外角等于它的内对角。【注释：它的内对角即和它相邻的内角的对角】
eg：∠C=∠BAE。
注意：性质1是定理，可直接使用；性质2选择、填空可用
例1-1、圆内接四边形ABCD中，∠A：∠B：∠C=1：2：3，则∠D=________。
解：设∠A的度数为x，则∠B的度数为2x，∠C的度数为3x,∵四边形ABCD是圆内接四边形，∴∠A+∠C=∠B+∠D=180°，∴x+3x=180°，解得：x=45°，∴∠B=2x=90°，∴∠D=90°。
∵AB是直径，∴∠ACB=90°，∴∠ABC=90°-∠CAB=55°。
例2、如图，四边形ABCD内接于⨀O，若∠C=130°，则∠BOD的度数为（　　）A．50°B．100°C．130°D．150°
解：∵四边形ABCD内接于⨀O，∠C=130°，∴∠A=180°-∠C=50°，∴∠BOD=2∠A=100°。
例3、如图，A、B、C是⨀O上三点，D是AB延长线上一点，∠CBD=65°，则∠AOC=________。
解：点E是优弧AB上一点（不与A、B重合），连接AE、CE，
根据题意可得：∠E+∠CBA=180°，∵∠CBD+∠CBA=180°，∴∠E=∠CBD=65°，∴∠AOC=2∠E=130°。
用假设法：其中三点确定一个圆，假设第四个点不在圆上
【思考1】在四边形ABCD中，∠B+∠D=180°，问：A、B、C、D四点共圆吗?
第四个点不在圆上，即第四个点在圆外或圆内
A、B、C三点可确定⨀O，①假设点D在圆外，
根据题意可得：∠B+∠AEC=180°，∵∠B+∠D=180°，∴∠AEC=∠D，与三角形的外角定理矛盾，故假设不成立。
设AD与⨀O交于点E，连接CE，
A、B、C三点可确定⨀O，②假设点D在圆内，
根据题意可得：∠B+∠E=180°，∵∠B+∠ADC=180°，∴∠E=∠ADC，与三角形的外角定理矛盾，故假设不成立。
延长AD交⨀O于点E，连接CE，
综上，点D在圆上，即A、B、C、D四点共圆。
【总结】如果四边形ABCD的一组对角互补，那么A、B、C、D四点共圆。
判定1：如果四边形ABCD的一组对角互补，那么A、B、C、D四点共圆。
eg：∵∠A+∠C=180°或∠B+∠D=180°，∴A、B、C、D四点共圆。
【思考2】在四边形ABCD中，∠ADB=∠ACB，问：A、B、C、D四点共圆吗?
设AD与⨀O交于点E，连接BE，
A、B、C三点可确定⨀O，②假设点D在圆外，
延长AD交⨀O于点E，连接BE，
【总结】如果四边形ABCD中，∠ADB=∠ACB，那么A、B、C、D四点共圆。
判定2：如果四边形ABCD中，∠ADB=∠ACB或∠BAC=∠BDC或∠CBD=∠CAD或∠DCA=∠DBA，那么A、B、C、D四点共圆。
eg：∵∠ADB=∠ACB或∠BAC=∠BDC或∠CBD=∠CAD或∠DCA=∠DBA，∴A、B、C、D四点共圆。
注意：判定1可直接使用；判定2选择、填空可用
例1、如图，在▱ABCD中，∠BAD为钝角，且AE⊥BC，AF⊥CD。（1）求证：A、E、C、F四点共圆；（2）设线段BD与（1）中的圆交于M、N，求证：BM=DN。
（1）证明：∵AE⊥BC，AF⊥CD，∴∠AEC=∠AFC=90°，∴∠AEC+∠AFC=180°，∴A、E、C、F四点共圆；
例1、如图，在▱ABCD中，∠BAD为钝角，且AE⊥BC，AF⊥CD。（2）设线段BD与（1）中的圆交于M、N，求证：BM=DN。
（2）证明：连接AC交BD于点O，由（1）可知：∠AEC=90°，∴AC是⨀O的直径，∵ABCD是平行四边形，∴OB=OD，O为圆心，∴OM=ON，∴OB-OM=OD-ON，即BM=DN。
例2、若在四边形ABCD中，∠BAC=∠BDC=30°，∠ACB=75°，则∠ADB=________。