初中2.4 圆周角习题ppt课件

这是一份初中2.4 圆周角习题ppt课件，共25页。PPT课件主要包含了°或120°，答案呈现，习题链接，答案D等内容，欢迎下载使用。

【2021·桂林】如图，AB是⊙O的直径，点C在⊙O上，连接AC，BC，则∠C的度数是(　　)A．60°　 B．90°C．120°　 D．150°
【2021·徐州】如图，AB是⊙O的直径，点C，D在⊙O上，若∠ADC＝58°，则∠BAC＝________°.
如图，AB是⊙O的直径，点C，D在⊙O上，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：①AD⊥BD；②∠AOC＝∠AEC；③BC平分∠ABD；④AF＝DF；⑤BD＝2OF；⑥△CEF≌△BED.其中一定成立的是(　　)A．②④⑤⑥ B．①③⑤⑥C．②③④⑥ D．①③④⑤
【点拨】∵AB是⊙O的直径，∴∠ADB＝90°，即AD⊥BD.因此①正确；∠AOC＝2∠ABC，∠AEC＝∠ABC＋∠BAD，若∠AOC＝∠AEC，则∠BAD＝∠ABC，则AC＝BD，而由已知无法推断出AC＝BD，因此②错误；∵OC∥BD，∴∠OCB＝∠CBD.∵OC＝OB，∴∠OCB＝∠OBC.∴∠CBD＝∠OBC.即BC平分∠ABD.因此③正确；
∵AD⊥BD，OC∥BD，∴OC⊥AD.∵点O为圆心，∴AF＝DF.因此④正确；∵AF＝DF，AO＝BO，∴BD＝2OF.因此⑤正确；若△CEF≌△BED成立，则CF＝BD，此时CF＝2OF，而由已知无法推断出CF＝2OF，故⑥错误，因此①③④⑤一定成立，故选D.
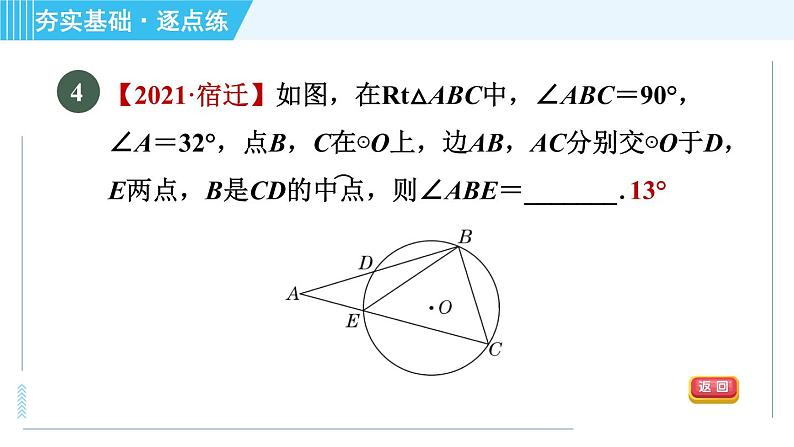
【2021·宿迁】如图，在Rt△ABC中，∠ABC＝90°，∠A＝32°，点B，C在⊙O上，边AB，AC分别交⊙O于D，E两点，B是CD的中点，则∠ABE＝_______．
【2021秋·泰州海陵区校级月考】如图，点P在以AB为直径的半圆内，连接AP，BP，并延长分别交半圆于点C，D，连接AD，BC并延长交于点F，作直线PF，下列说法：①BD⊥AF；②AC平分∠BAF；③FP⊥AB；④FP平分∠AFB.其中一定正确的序号为________．
【点拨】如图，当点P(P1)在弦AB所对的优弧上时，过点O作OC⊥AB于点C，连接OA，OB.由垂径定理可得AC＝2，∠AOC＝∠BOC.
【2021春·盐城亭湖区校级期末】如图，在△ABC中，AB＝AC，以AB为直径的半圆O分别交AC，BC于点D，E.
(1)求证：E是BC的中点；
证明：连接AE，∵AB是⊙O的直径，∴∠AEB＝90°，即AE⊥BC，∵AB＝AC，∴BE＝CE，即E是BC的中点.
(2)若∠BOD＝75°，求∠CED的度数．
【2020秋·扬州期末】如图，AB是⊙O的直径，C是BD的中点，CE⊥AB于点E，BD交CE于点F.
(1)求证：CF＝BF；
证明：∵AB是⊙O的直径，∴∠ACB＝90°，又∵CE⊥AB，∴∠CEB＝90°.∴∠2＝90°－∠ABC＝∠A.又∵C是BD的中点，∴∠1＝∠A.∴∠1＝∠2.∴CF＝BF.
(2)若CD＝12，AC＝16，求⊙O的半径和CE的长．
如图，已知ED是⊙O的直径且ED＝4，A(不与点E，D重合)是⊙O上一个动点，线段AB经过点E，且EA＝EB，F是⊙O上一点，∠FEB＝90°，BF的延长线与AD的延长线交于点C.
(1)求证：△EFB≌△ADE；
证明：如图，连接FA.∵∠FEB＝90°，∴EF⊥AB.∵BE＝AE，∴BF＝AF.∵∠FEA＝∠FEB＝90°，∴AF是⊙O的直径．∴AF＝DE.∴BF＝ED.∵DE是⊙O的直径，∴∠EAD＝90°.
(2)当点A在⊙O上移动时，直接回答四边形FCDE的最大面积为多少．
解：四边形FCDE的最大面积为8.
【中考·宜昌】如图，在△ABC中，AB＝AC，以AB为直径的半圆形交AC于点D，交BC于点E，延长AE至点F，使EF＝AE，连接FB，FC.
(1)求证：四边形ABFC是菱形；
证明：∵AB为半圆形的直径，∴∠AEB＝90°.∵AB＝AC，∴CE＝BE.又∵EF＝AE，∴四边形ABFC是平行四边形.又∵AB＝AC，∴平行四边形ABFC是菱形.
(2)若AD＝7，BE＝2，求半圆形和菱形ABFC的面积．
解：设CD＝x，则AB＝AC＝7＋x，∵CE＝BE＝2，∴BC＝4.连接BD，如图，