高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质示范课ppt课件

这是一份高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质示范课ppt课件，共25页。

　　德国著名的心理学家艾宾浩斯对人类的记忆牢固程度进行了有关研究.他经过测试,得到了有趣的数据.数据表明,记忆量y是时间间隔t的函数.艾宾浩斯根据这些数据描绘出了著名的“艾宾浩斯记忆遗忘曲线”,如图:
问题　(1)当时间间隔t逐渐增大时,你能看出对应的函数值y有什么变化趋势吗?
(2)“艾宾浩斯记忆遗忘曲线”从左至右是逐渐下降的,对此,我们如何用数学的观点进行解释?
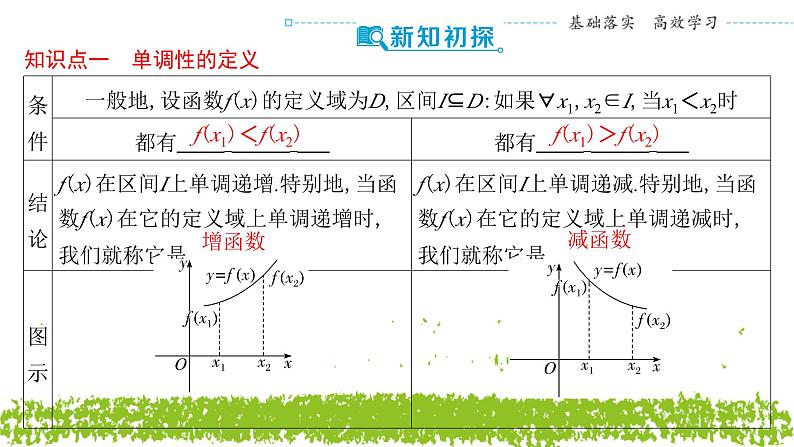
知识点一　单调性的定义
f(x1)＜f(x2)　
f(x1)＞f(x2)　
提醒　(1)函数的单调递增(单调递减)是针对定义域D内的某个区间I而言的,显然I⊆D;(2)定义中x1,x2有三个特征:①x1,x2属于同一个区间;②任意性,x1与x2不能用I上的特殊值代替;③有序性,通常规定x1＜x2.
　在单调性的定义中,能否把“∀x1,x2∈I ”改为“∃x1,x2∈I ”?
提示:不能,如图所示,虽然f(-1)＜f(2),但原函数在[-1,2]上不单调.
知识点二　函数的单调区间　如果函数y＝f(x)在区间I上 　单调递增　⁠或 　单调递减　⁠,那么就说函数y＝f(x)在这一区间具有(严格的)单调性,区间I叫做y＝f(x)的 　单调区间　⁠.
　区间I一定是函数的定义域吗?
提示:不一定,可能是定义域的一部分.
1.下列函数中,在区间(0,1)上单调递增的是(　　)
2.若函数f(x)＝(2a-1)x＋b在R上是减函数,则有(　　)
3.函数f(x)＝-x2＋2x＋3的单调递减区间为 　　　　⁠. 
解析:易知二次函数f(x)＝-x2＋2x＋3的图象开口向下,其对称轴为直线x＝1,所以其单调递减区间是[1,＋∞).
利用定义证明函数单调性的4步骤
【例2】　画出函数f(x)＝-x2＋2｜x｜的图象,根据图象写出函数f(x)的单调区间.
解　如图所示,由图象可知函数f(x)的单调递增区间是(-∞,-1),(0,1),
函数的单调递减区间是(-1,0),(1,＋∞).
通性通法求函数单调区间的2种方法(1)定义法:即先求出定义域,再利用定义法进行判断求解;(2)图象法:即先画出图象,根据图象求单调区间.提醒　(1)如果函数f(x)在其定义域内的两个区间A,B上单调性相同,则两个区间用“,”或“和”连接,不能用“∪”连接;(2)书写单调区间时,若函数在区间的端点处有定义,则写成闭区间、开区间均可,但若函数在区间的端点处无定义,则必须写成开区间.
　画出函数y＝｜x｜(x-2)的图象,并指出函数的单调区间.
由函数的图象知,函数的单调递增区间为(-∞,0]和[1,＋∞),单调递减区间为(0,1).
角度一:已知函数的单调性求参数
通性通法已知函数的单调性求参数范围的一般思路(1)将参数看成已知数,求函数的单调区间,再与已知的单调区间比较,求出参数的范围;(2)运用函数单调性的定义建立关于参数的不等式(组),解不等式(组)求出参数的范围.
角度二:利用单调性解不等式
【例4】　已知f(x)在区间[-2,2]上单调递增,且f(x-2)＜f(1-x),则x的取值范围为 　　　　⁠. 
通性通法利用单调性比较大小或解不等式的方法(1)利用函数的单调性可以比较函数值或自变量的大小;在解决比较函数值的问题时,要注意将对应的自变量转化到同一个单调区间上;(2)在求解与抽象函数有关的不等式时,往往是利用函数的单调性将“f”脱掉,使其转化为具体的不等式求解.此时应特别注意函数的定义域.
2.已知函数f(x)＝x2＋ax＋b在区间(-∞,1]上单调递减,在区间[1,＋∞)上单调递增,且f(m＋2)＜f(2),则实数m的取值范围为 　　　　⁠. 
1.什么叫函数的单调性？你能举出一些具体例子吗？
3.结合本节课放入学习过程你对函数性质的研究内容和方法有什么体会？
2.你认为在理解函数单调性的时候应把握好哪些关键问题？
1.(多选)如图所示的是定义在区间[-5,5]上的函数y＝f(x)的图象,则下列关于函数f(x)的说法正确的是(　　)
解析:ABD　若一个函数出现两个或两个以上的单调性相同的区间,不能用“∪”连接.故选A、B、D.
2.函数y＝｜x｜-1的单调递减区间为 　　　　⁠. 
解析:当x＞0时,y＝｜x｜-1＝x-1,此时函数单调递增,当x≤0时,y＝｜x｜-1＝-x-1,此时函数单调递减,即函数的单调递减区间为(-∞,0].
4.已知函数y＝f(x)是(-∞,＋∞)上的增函数,且f(2x-3)＞f(5x-6),则实数x的取值范围为 　　　　⁠.若该函数f(x)是定义在(0,＋∞)上的减函数,则x的取值范围为 　　　　⁠.