







高中数学人教A版 (2019)必修 第一册第三章 函数的概念与性质3.4 函数的应用(一)优质学案
展开函数的性质综合
学习目标
1. 理解函数的对称性、周期性;
2. 能够解决函数的单调性、奇偶性、对称性、周期性综合的问题.
【备注】本节重点:函数的对称性和周期性;
本节难点:对称性与周期性综合,单调性与对称性综合;
前置知识:函数的概念,函数的单调性和奇偶性;
后置知识:基本初等函数,三角函数.
一、 函数图象的变换
1. 平移变换
的图象向上平移 个单位(横坐标不变)得到
的图象;
的图象向下平移 个单位(横坐标不变)得到的图象;
的图象向左平移 个单位(纵坐标不变)得到的图象;
的图象向右平移 个单位(纵坐标不变)得到的图象.
2. 对称变换
同样利用平移变换中那种相关点的方法讨论,不难得到:
可由的图象沿 轴做轴对称得到的图象;
可由的图象沿 轴做轴对称得到的图象;
可由的图象沿原点做中心对称得到的图象.
3. 翻折变换(一)可得
的图象的做法是:
①将图象位于 轴上方的部分保留,
②把位于 轴下方的图象沿 轴做轴对称翻折至 轴的上方,③并将位于 轴下方的部分去掉.
(二)可得的图象的做法是:
①将图象位于 轴右侧的部分保留,
②位于 轴左侧的部分去掉,
③并把位于 轴右侧的图象沿 轴做轴对称至 轴的左侧.
经典例题
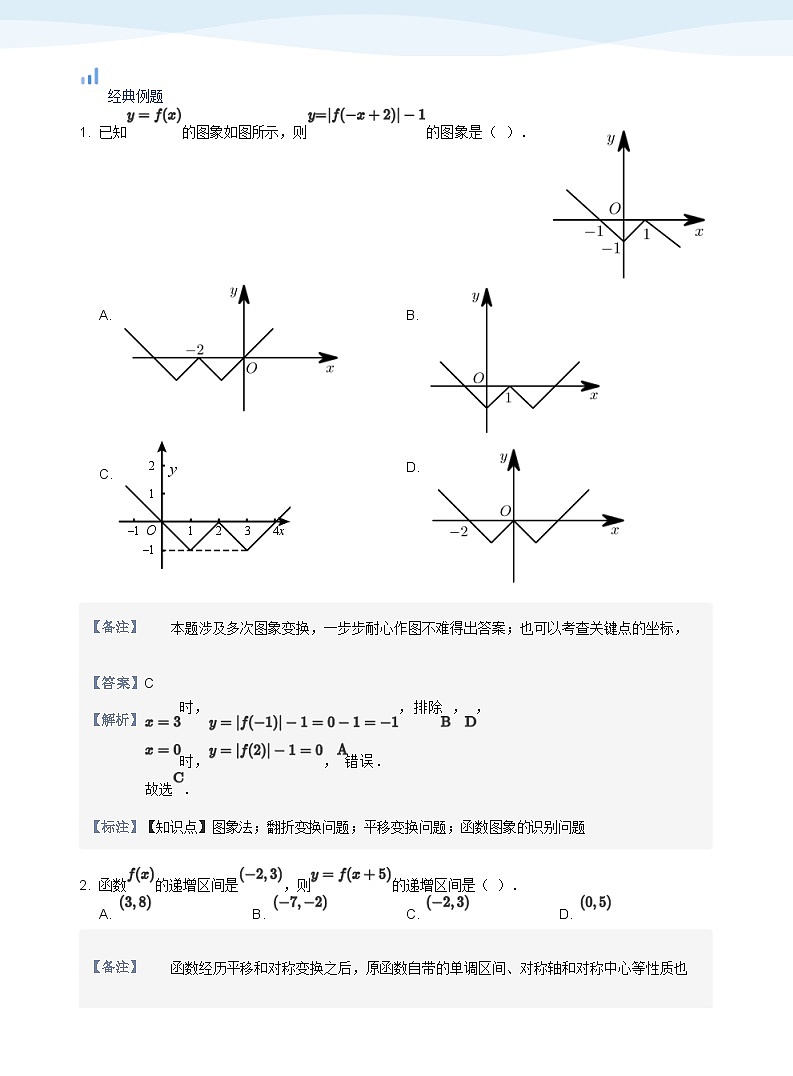
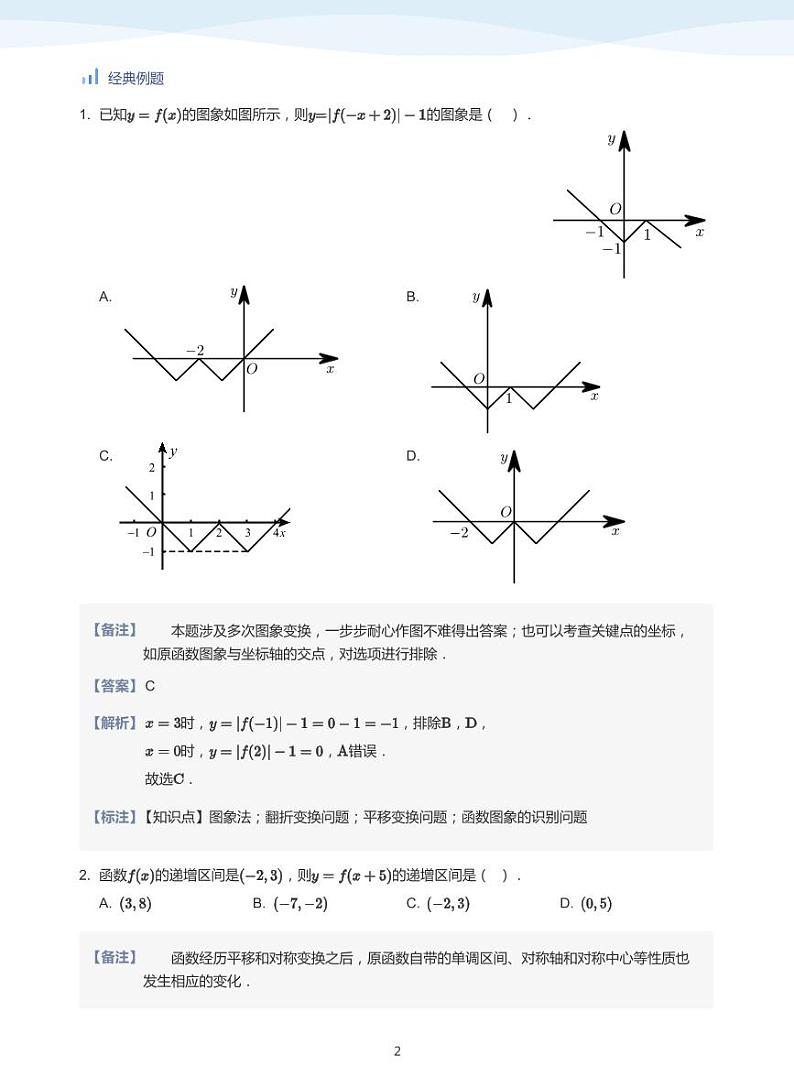
1. 已知的图象如图所示,则的图象是( ).
A.B.
C.
2
1
y
D.
–1
O
–1
1
2
3
4x
【备注】
本题涉及多次图象变换,一步步耐心作图不难得出答案;也可以考查关键点的坐标,
【答案】C
【解析】
时,
,排除 , ,
时,, 错误.
故选 .
【标注】【知识点】图象法;翻折变换问题;平移变换问题;函数图象的识别问题
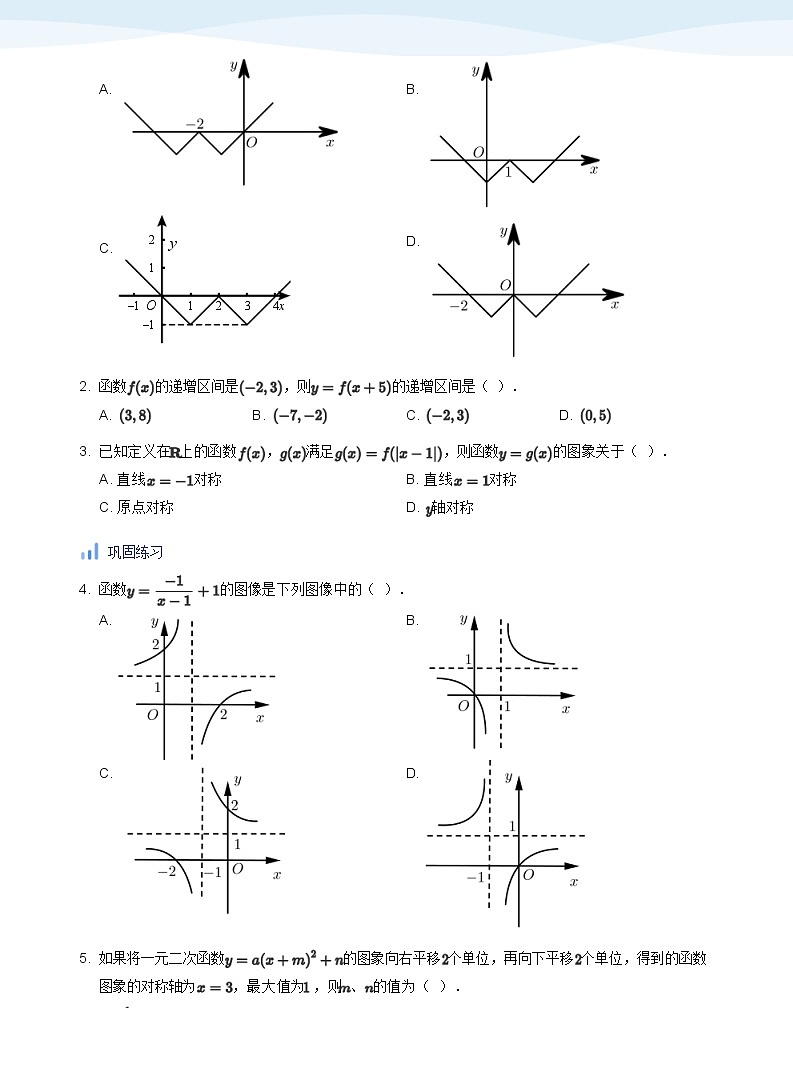
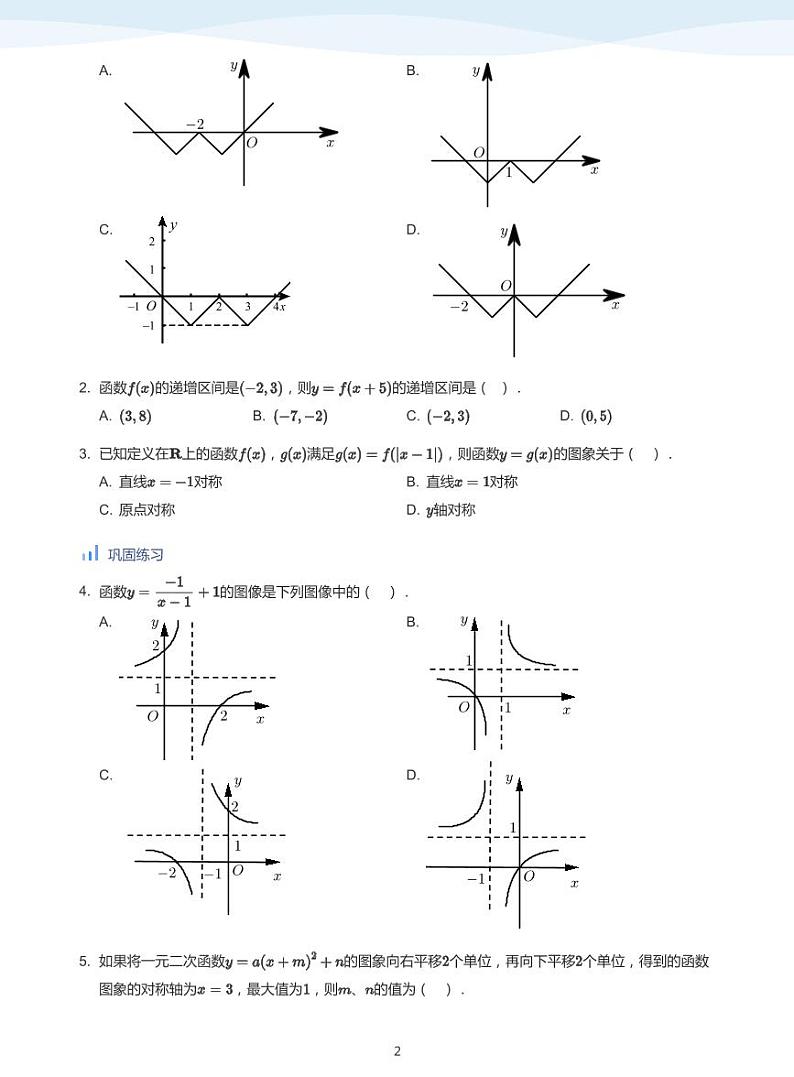
2. 函数的递增区间是,则的递增区间是( ).
A.B.C.D.
【备注】
函数经历平移和对称变换之后,原函数自带的单调区间、对称轴和对称中心等性质也
【答案】B
【解析】函数
是函数
向左平移 个单位得到的,
∵函数在区间上是增函数,
∴增区间为向左平移 个单位,即增区间为.
故选 .
【标注】【知识点】用定义法证明函数的单调性
3. 已知定义在 上的函数, 满足,则函数的图象关于( ).
A. 直线对称B. 直线对称
C. 原点对称D. 轴对称
【备注】 结合函数图象变换思考,可先关于 轴作对称变换再向右平移一个
单位长度,对称变换产生的对称轴,向右平移就得到新对称轴.
如从定义出发,也不难看出,可知对称轴为.
【答案】B
【解析】法一:由
关于 轴对称,由
向右平移一个单位可得
,即函数
的图像关于对称;
法二:特殊处理,令,则,该图像关于对称.
【标注】【知识点】平移变换问题;一个函数的自对称问题
巩固练习
4. 函数的图像是下列图像中的( ).
A.B.
C.D.
【答案】A
【解析】首先作为分母
,
∴, , 错误,
其次令,
,
图象在第二、四象限,
∴选 .
或令,代入,
时,,排除 、 ,
时,,排除 .
【标注】【知识点】平移变换问题;图象法
5. 如果将一元二次函数的图象向右平移 个单位,再向下平移 个单位,得到的函数
图象的对称轴为,最大值为 ,则 、 的值为( ).
A. B. C. D.
【答案】D
【解析】由题意知,变换后所得函数的解析式为
,且
,
然后将函数的图象先向上平移 个单位,
得到函数,
再将所得函数图象向左平移 个单位,
可得到函数的图象,
因此.
故选: .
【标注】【知识点】平移变换问题;含参二次函数的图象及性质
6. 已知函数,则在同一个坐标系下函数与的图象不可能是(
).
A.B.
C.D.
【答案】D
【解析】
,
( )若,则当时,对称轴为,开口向上,
当时,对称轴为,开口向下,
∴在上单调递增,在上单调递增,且,
是由向左平移 个单位得到的,
此时函数图象为 ,
( )若,则当时,对称轴为,开口向下,
时,对称轴为,开口向上,
∴在上先增后减,在上先减后增,且,
是由向右平移 个单位得到的,
此时函数图象为 或 ,故选: .
【标注】【知识点】图象法
二、 函数的对称性
1. 一个函数的自对称问题
(1)关于 轴对称
;
(2)关于原点对称;
(3)关于直线对称或;
(4)关于点对称或.
经典例题
7. 若函数
的图象关于直线
对称,则
的最大值为
.
【备注】 已知函数对称性求参数,特殊值法是很常用也很便捷的方法,本题中涉及求高次函数
的最值,,观察到出现了()整体可供换
元,这样的方法比较适合高一学生.
【答案】
【解析】方法一:∵函数
的图象关于直线
对称,
∴且,
即且,
解之得,
因此,,
求导数,得,
令,得,,,
当时,.
当时,.
当时,.
当时,.
∴在区间、上是增函数,在区间、
上是减函数.
又∵,
∴的最大值为 .
方法二:因为函数关于
对称,由函数与 轴交点坐标知道 为解,则还有 ,
也为其解,则
,则当原式取得最大值 ,
故答案为: .
【标注】【素养】数学运算;逻辑推理
【知识点】求函数最值(含参二次型导函数);一个函数的自对称问题
8. 函数的对称中心为( ).
A.,B.,C.,D.,
【备注】
寻找函数的对称中心和对称轴,通常可采取先猜后证的方法,尤其对于选择题,可以
在猜对称中心时,常用的技巧是从定义域入手,具有对称性的函数,其定义域也与对
关于对称,因此不难猜出对称
,可以猜想对称中心纵坐标为 ,分离常数的处
【答案】B
【解析】∵函数
,
∴
,
∴,
即函数
故选 .
【标注】【知识点】一个函数的自对称问题
的对称中心为
,
.
9.
已知函数满足,若函数与图象的交点为,
, ,,则( ).
A.B.C.D.
【备注】 两函数都关于对称,他们的交点也是一对对关于对称的点.
【答案】B
【解析】函数
,(
)满足
,
即为,
可得关于点对称,
函数,即的图象关于点对称,
即有为交点,即有也为交点,为交点,即有也
为交点,
则
原式
.
故选 .
【标注】【知识点】两个函数的互对称问题
巩固练习
10. 已知函数的图象关于点 中心对称,则点 的坐标是.
【答案】
【解析】
,
∵函数的图象关于点 中心对称,
∴点 的坐标是,
故答案为.
【标注】【知识点】一个函数的自对称问题
11.
已知定义在 上的函数的图象关于对称,,若函数图象与函数
图象的交点为,, ,,则( ).
A.B.C.D.
【答案】C
【解析】∵
的图象是由
的函数图象先向右平移 个单位,再向上平移 个单位后得到的,
∴ 的图象关于点对称,
又的图象关于点对称,
∴与 的个交点中,两两关于点对称.
∴.
故选: .
【标注】【知识点】两个函数的互对称问题
12. 设满足:①任意,有;②当时,,
,若
A.
,
,恒有
B.
,
,则 的取值范围是( ).
C.,
D.
,
【答案】B
【解析】∵任意
,有
.
∴,
则函数关于 , 点对称,
当时,,即,
则,
∵当时,,
∴,
则,则或,
则或,
∵,
∴,即当时,,
当时,,,
即,,
作出函数的图像如图:
若,则由图像知,将函数向右平移 个单位即可,
由图像知,.
【标注】【知识点】利用函数性质画简图
2. 两个函数的互对称问题
(1)与关于 轴 对称.
(2)与关于 轴 对称.
(3)与关于 原点 对称.
(4)与关于 直线对称.
(5)与关于 直线对称.
(6)与关于对称.
(7)函数与的图象关于 直线对称.
经典例题
13. 若定义域均为 的三个函数, ,满足条件,点与点都关于点
对称,则称是 关于的“对称函数”.已知,,
是 关于的“对称函数”,且恒成立,则实数 的取值范围是( ).
A.B.
C.D.
【备注】 不难分析出,本题须满足即恒成立,高一学生可用
判别式法解此恒成立问题:定义域上,恒成立且
恒成立.
【答案】D
【解析】当题可知,
即,
当
,必有
,
此时,不满足
,
所以,由图可知,
直线
与
相切或相离且
在 上方,
显然.
由点到直线距离可知
.
【标注】【素养】数学运算
【知识点】两个函数的互对称问题【知识点】直线与圆的位置关系
14. 已知函数与的图象上存在关于 轴对称的点,则实数 的取
值范围是( ).
A.B.
C.D.
【备注】存在关于 轴对称的点等价于方程在上有实根,
可用参变分离处理.
【答案】A
【解析】若函数
则方程
与
的图象上存在关于 轴对称的点,
在区间上有解,
令,,
由的图象是开口朝上,且以直线为对称轴的抛物线,
故当时,取最小值 ,当时,函数取最大值 ,
故.
故选 .
【标注】【知识点】函数零点的概念;已知零点情况求参数的取值范围
巩固练习
15. 设函数定义在实数集上,则函数与的图像关于( ).
A. 直线对称B. 直线对称C. 直线对称D. 直线对称
【答案】C【解析】略
【标注】【知识点】两个函数的互对称问题
16. 已知函数与的图象上存在关于 轴对称的点,则实数 的取
值范围是( ).
A.B.
C.D.
【答案】A
【解析】由题意知
在
上有解,
及在上有解,
即在上有解,
易知在上的值域为,
所以 的取值范围为.
【标注】【知识点】已知零点情况求参数的取值范围;函数零点的概念
17. 设曲线 的方程是,将 沿 轴、 轴正方向分别平移 、个单位长度后得到曲线
,
( 1 )写出曲线 的方程.
( 2 )证明曲线 与 关于点对称.
( 3 )如果曲线 与 有且仅有一个公共点,证明:
.
【答案】( 1 )
( 2 )证明见解析.
.
( 3 )证明见解析.
【解析】( 1 )曲线 的方程为
.
( 2 )在曲线 上任意取一点,设是 关于点 的对称点,
则有,,
∴,代入曲线 的方程 ,
得 , 的方程 :,
即可知点在曲线 上.
反过来,同样证明,在曲线 上的点 的对称点在曲线 上.因此,曲线 与 关于点 对称.
( 3 )由于曲线 与 有且仅有一个公共点,
∴方程组有且仅有一组解,
消去 ,整理得,这个关于 的一元二次方程有且仅
有一个根,
则
,即得
,
因为,所以.
【标注】【知识点】解析法;两个函数的互对称问题;零点、交点、根的等价转化;函数零点的概
念;平移变换问题
3. 对称性与单调性综合
对称性与单调性综合的研究方法可以类比单调性与奇偶性综合,不论是比较大小还是解不等式,一
般方法是利用数形结合的思想,都是将待求的点利用对称性转化到一个单调区间上.
经典例题
18. 已知定义域为 的函数在区间上单调递减,对任意实数 ,都有,
那么下列式子一定成立的是( ).
A. B. C. D.
【备注】 类比偶函数和单调性综合,利用对称性,将待比较的各点都转化到递减区间
上.
【答案】C【解析】
∵
,
∴函数的图象关于对称,
∴,
∵函数在区间上单调递减,
∴在)上为单调递增.
∴,
即,
故选 .
【标注】【知识点】单调性;抽象函数
19. 已知定义域为 的函数满足,且函数在区间上单调递增,
如果,且,则的值( ).
A. 恒小于B. 恒大于C. 可能为D. 可正可负函数
【备注】 除如解析中推导外,不妨令满足关于点对称,且在上单
调递增.
【答案】B
【解析】∵定义域为 的函数
∴函数的图象关于
即,
,且
则,
∵函数在区间
∴,
∴,
∴.
故选: .
满足
对称,
,
上单调递增,
,
【标注】【知识点】函数对称性与单调性综合问题
巩固练习
20. 已知函数满足,且在上是增函数,如果,
则与的不等式关系为.
【答案】
【解析】
,所以
图像关于
对称,
又在上是增函数,所以图像上的点到直线的距离越远越大,
说明 离更近,所以.
【标注】【知识点】抽象函数
21. 已知定义在 上的函数关于点中心对称,当时,单调递增,若且
,则的值( ).
A. 恒大于B. 恒小于C. 可能为D. 可正可负
【答案】B
【解析】设
,由
,
得,,再由得:
,
∵时,单调速增,
∴,
∵函数关于点对称,
∴,
取得,
∴,
即.
故选 .
【标注】【知识点】函数对称性与单调性综合问题
22.
已知函数满足:,,且 ,,
,则( ).
A. B. C.
,
D. 若,则
【答案】BC
【解析】由
,
,
,可得
图象关于
对
称,
由 ,
,
可得
在
单调递减,
结合单调性、对称性,可知距越近函数值越大,
则显然 不正确, 正确,
选项,
, 正确;
选项,时, 距更远,则或, 错误.
故选 .
【标注】【知识点】函数对称性与单调性综合问题
4. 对称性与最值综合
在《函数奇偶性及其应用》一讲,我们讲到过:对于奇函数
而言,
的最大值 和
的
最小值 ,有.
这一性质可以进一步推广到有对称中心的函数.假设
,即函数
关于点
对称,则函数在关于直线对称的区间上的最大值 和最小值 ,满足.
若在处有意义,则.
经典例题
23. 定义在
上的函数
满足:对于任意 ,,有
,若的最大值和最小值分别为 、 ,则
的值
为.
【备注】关于中心对称,即可快速得出答案.
【答案】
【解析】令
,则
,令
,
,则
,
∴,令,
∴,为奇函数,
∴,.
【标注】【知识点】求抽象函数的最值
巩固练习
24. 已知函数在区间的最大值为 ,最小值为 ,若
,则.
【答案】
【解析】
,
设,
∵,
∴,
又∵为常数,时,时,,
∴,.
故答案为: .
【标注】【知识点】利用奇偶性求值;利用定义判断函数奇偶性
三、 函数的周期性
1. 周期性的判定与简单应用
函数的周期性需要抓住以下两点,一是定义:对定义域中任意的 恒有
;二是找周
期:能找到适合这一等式的非零常数 .
一般来说,周期函数的定义域均为无限集,迭代法是判断周期性的常用方法,
关于函数的周期性有如下推广结论,均可用迭代法推导证明:
若函数满足如下关系,则的周期为
①
② ③ ④
.
经典例题
25. 已知是定义在 上的函数,且,若,则
.
【备注】 求大值离散点对应的函数值,常常要用到周期性,在没有头绪的时候,不妨多写几
项.
【答案】
【解析】
,
,
,
,
∴,
∴周期为 ,
∴.
【标注】【知识点】利用函数周期性求函数值
26. 已知函数是周期为 的函数,当时,,当时,的解
析式是.
【备注】 求周期函数某一周期的解析式,要点是求哪个周期,就设自变量 在哪个周期,利用周
期性,使落在已知解析式的周期内,代入计算即可 .
【答案】
【解析】
当时,,
所以.
【标注】【素养】数学抽象;数学运算
【知识点】利用函数周期性求函数值
27. 设 是定义在 上,以 为周期的函数,若函数在区间上的值域为,
则在区间上的值域为.
【备注】 构建类周期函数是本题的核心步骤,需要注意的是,由于
在一个周期内的单调性未知,因此不能直接指定端点值计算.
【答案】
【解析】当
时,
,
,
由
,可得;
当时,,,
由,
可得.
所以在区间上的值域为.
【标注】【知识点】用单调性观察法求值域
巩固练习
28.对于任意实数 满足条件,若,则( ).
A.B.C.D.
【答案】B
【解析】∵
,
∴,
∴是以 为周期的函数,
∴,
又∵,
∴,
故选 .
【标注】【知识点】利用函数周期性求函数值
29. 已知函数满足:, ,且,则(
).
A.B.C.D.
【答案】A
【解析】∵
,
∴令,得,
即,
即①,
用替换 ,得②,
① ②得:,
再用替换 ,得.
∴,
函数是周期的周期函数.
因此,.
∵,
∴令,得,可得.
在中令,
得,
∴,解得,
同理在中令,
解得.
∴.
故选 .
【标注】【素养】数学运算;逻辑推理
【知识点】利用函数周期性求函数值;迭代法判断周期;抽象函数
30. 已知是定义在 上的函数,且,
( 1 )试证( 2 )若
是周期函数;
,求
。
【答案】( 1 )依次求出
为
( 2 )
【解析】( 1 )依次求出
为
( 2 )
( ), (
( ), (
), (
), (
), (
), (
)即可,发现周期
)即可,发现周期
【标注】【知识点】利用函数周期性求函数值;迭代法判断周期
2. 周期性与奇偶性、对称性综合
函数满足对定义域内任一实数 (其中 为常数):
(1)函数满足(),若为奇函数,则其周期为,若
为偶函数,则其周期为.
(2)函数的图象关于直线和都对称,则函数是以为
周期的周期函数.
(3)函数
的图象关于两点
,
都对称,则函数
是以
为周期的周期函数.
(4)函数的图象关于和直线都对称,则函数是以
为周期的周期函数.
经典例题
31. 已知定义在 上的奇函数的满足,且,则( ).
A.B.C.D.
【备注】 由对称轴和对称中心,可知该函数周期为 ,记住结论可以减少做题时耗;
本题推导起来也不麻烦,只需用对称性和奇函数的性质交替迭代即可得到周期,如下:
.
【答案】A
【解析】为 上的奇函数,
∴且关于中点对称,
又∵,
∴关于直线对称,
∴的最小正周期,
∴.
【标注】【知识点】奇偶性;函数周期性与奇偶性综合问题
32. 已知是定义域为的奇函数,满足,若,则
( ).
A.B.C.D.
【备注】 由奇函数(对称中心)和对称轴,易得周期为 ,每四个一组求和,最后加
上"零头"即可.
【答案】C
【解析】是奇函数,且,
,
∴,∴,
即函数
是周期为 的周期函数,,
,
,
则,
则
,
故选 .
【标注】【知识点】函数周期性与奇偶性综合问题;奇偶性
巩固练习
33. 已知是定义在 上的函数,且对任意都有,若函数
的图象关于点对称,且,则( ).
A.B.C.D.
【答案】D
【解析】因为函数
的图象关于点
对称,
所以函数的图象关于点对称,是奇函数.
对任意都有,
令,即,得.
由知,
所以是周期为 的周期函数,
.
故选 .
【标注】【知识点】奇偶性
34.是定义在 上的以 为周期的奇函数,且,则方程在区间内解的个数的
最小值是( )
A.B.C.D.
【答案】D
【解析】
是定义在 周期为 的奇函数,∴
,
,∴,∴选D.
【标注】【知识点】函数周期性与奇偶性综合问题;求零点个数问题(不含参)
35. 函数的定义域为 ,若与都是奇函数,则( ).
A.是偶函数B.是奇函数
C.D.是奇函数
【答案】D
【解析】方法一:
与
都是奇函数,
,,
即,
函数关于点,及点对称,函数是周期的周期
函数.
,,则是奇函
数.
故选 .
方法二:函数
的图像是由函数
的图像向左平移 个单位长度得到的,因为
是奇函数,所以的图像关于原点对称,因此的图像一定关于点
成中心对称,即.函数也是奇函数,所以同理,
关于点成中心对称,即,所以
,因为
是奇函数,所以也是奇数.
故选 .
【标注】【素养】数学运算
【知识点】周期性
【知识点】函数单调性与奇偶性综合问题【知识点】对称性
四、 函数性质大杂烩
经典例题
36. 定义在 上的偶函数满足:,且在上是增函数,下面关于的判断:
①是周期函数;
②的图象关于直线对称;
③在上是减函数;
④在是减函数.
其中正确的判断是.(把你认为正确的判断都填上)
【备注】 需要指出的是,可得函数的周期性,再结合偶函数(对称轴),
可以求得函数存在对称中心,相邻对称轴(对称中心)之间的距离为半个周期.轴对称的
两段函数增减性相反,中心对称的两端函数增减性相同,可类比奇偶性与单调性的综合.
【答案】①②③
【解析】
,所以函数
是以 为周期的偶函数,所以①正确;
,所以②正确;
又函数在上是增函数,关于直线对称,所以在上是减函数,所以
③正确;
因为
是偶函数,所以
在
上是增函数,所以④错误;
综上,①②③正确.
【标注】【知识点】抽象函数
37. 已知函数的定义域为 ,且满足下列三个条件:
①对任意的,当时,都有恒成立;
②;③是偶函数;
若,,,则 , , 的大小关系正确的是( ).
A.B.C.D.
【备注】
对题干条件一一翻译是解决此类包含多种函数性质的题目的关键,要最终实现比较大
【答案】B
【解析】由①知,函数
在区间
上为增函数,
由②知,,即函数的周期为 ,
由③知,函数的图象关于直线对称,
,,
,故;
故选 .
【标注】【知识点】函数周期性与奇偶性综合问题
38. 已知是定义在 上的奇函数,满足,当时,,则下列
结论错误的是( ).
A. 方程最多有四个解
B.
C.
D.
函数
函数
的值域为
的图象关于直线
对称
【备注】
y
–2
–1
2
1
O
–1
–2
1
2
3
x
针对选项 的讨论可以数形结合的方式进行:
不难发现,如直线与函数最多有 个交点.
【答案】A
【解析】 .由
可得:
,
则,所以函数的周期为 ,
所以,故 正确;
.再由以及,
所以,则函数的对称轴为,故 正确;
.当时,,
又函数是奇函数,时,,
即时,
又因为函数的对称轴为,
所以时,
所以时,
又因为函数的周期为 ,
所以函数的值域为,故 正确.
故选 .
【标注】【知识点】函数周期性与奇偶性综合问题
巩固练习
39. 已知是定义在 上的奇函数,是偶函数,当时,单调递减,则下面关
于
A.
的判断正确的是( ).
的一个周期是
B. C. D.
在
是
单调递增
的一个对称中心
【答案】ABD
【解析】由题意,函数
是定义在 上的奇函数,可得
,
又由是偶函数,可得其图象关于 轴对称,
根据函数的图象变换,可得函数关于对称,即,
联立可得,即,即,
所以函数的一个周期是 ,故 正确;
又由当时,单调递减,根据函数是定义在 上的奇函数,
可得当时,单调递减,再由函数关于对称,
可得在单调递增,故 正确;
由函数是定义在 上的奇函数,可得,
即原点为函数的一个对称中心,又由函数关于对称,且周期,
可得,,,,且,为函数的对称中心,
故 不正确, 正确.
故选.
【标注】【方法】定义法
【知识点】函数周期性与奇偶性综合问题;函数对称性与周期性综合问题
40. 定义在 上的函数满足,,且在区间上是减函
数,设,,,则 , , 的大小顺序是( ).
A.B.C.D.
【答案】A【解析】
具有周期性,
,
将所示换至同一单调区间比较,
且偶函数,
,,
,
,
∵,且在上,
∴,
即.
【标注】【知识点】函数周期性与奇偶性综合问题
41. 已知定义在 上的偶函数满足:,对,当时,
,且,则不等式在上的解集为.
【答案】
【解析】由题意,
在
上单调递减,而
,由偶函数得:当
时,
,
又可得周期,
所以当时,,
于是的解集为.
【标注】【知识点】利用函数单调性解不等式;函数周期性与奇偶性综合问题;函数对称性与周期
性综合问题
导图总结
你学会了吗?快用思维导图来总结本节课所学吧!
【备注】
出门测
42. 设是定义在 上以 为周期的函数,在内单调递减,且的图象关于直线对
称,则下面正确的结论是( ).
A.B.
C.D.
【答案】B
【解析】
是以 为周期的函数,即
,
.
又的图象关于直线对称,,,
又在上单调递减,,
即.
【标注】【知识点】函数对称性与单调性综合问题;用单调性比较大小;利用函数周期性求函数值
43. 已知函数的定义域为 .当时,;当时,;当
时,.则( ).
A.B.C.D.
【答案】D
【解析】因为当
时,
,
所以,
所以当时,周期为 ,
故有,
因为当时,,
所以当时,是奇函数,
故而,
因为当时,,
所以,
则有.
故选 .
【标注】【知识点】奇偶性
44. 已知是 上的奇函数,对都有成立,若,则等
于().
A.B.C.D.
【答案】C
【解析】∵
是 上的奇函数,对
都有
)成立,
∴可令,则,
解得,而,
∴.
∴.
∴.
故选 .
【标注】【知识点】函数周期性与奇偶性综合问题;利用函数周期性求函数值
【素养】数学运算
45. 设是定义在 上且周期为 的函数,在区间上其中,
若,则的值是.
【答案】
【解析】∵
是周期为 的函数,
∴,
.
又∵,
所以,
即,解得,
则.
【标注】【知识点】函数求值问题;分段函数
31
必修 第一册5.4 三角函数的图象与性质学案: 这是一份必修 第一册<a href="/sx/tb_c4000283_t4/?tag_id=42" target="_blank">5.4 三角函数的图象与性质学案</a>,文件包含三角函数的图象与性质-讲义教师版docx、三角函数的图象与性质-讲义学生版docx等2份学案配套教学资源,其中学案共45页, 欢迎下载使用。
数学必修 第一册数学建模 建立函数模型解决实际问题学案: 这是一份数学必修 第一册<a href="/sx/tb_c4037448_t4/?tag_id=42" target="_blank">数学建模 建立函数模型解决实际问题学案</a>,文件包含函数的应用零点与函数模型-讲义教师版docx、函数的应用零点与函数模型-讲义学生版docx等2份学案配套教学资源,其中学案共47页, 欢迎下载使用。
数学3.3 幂函数学案设计: 这是一份数学<a href="/sx/tb_c4000269_t4/?tag_id=42" target="_blank">3.3 幂函数学案设计</a>,文件包含幂函数与对勾函数-讲义教师版docx、幂函数与对勾函数-讲义学生版docx等2份学案配套教学资源,其中学案共27页, 欢迎下载使用。














