





人教A版 (2019)第三章 函数的概念与性质3.2 函数的基本性质优秀学案
展开函数的奇偶性及其应用
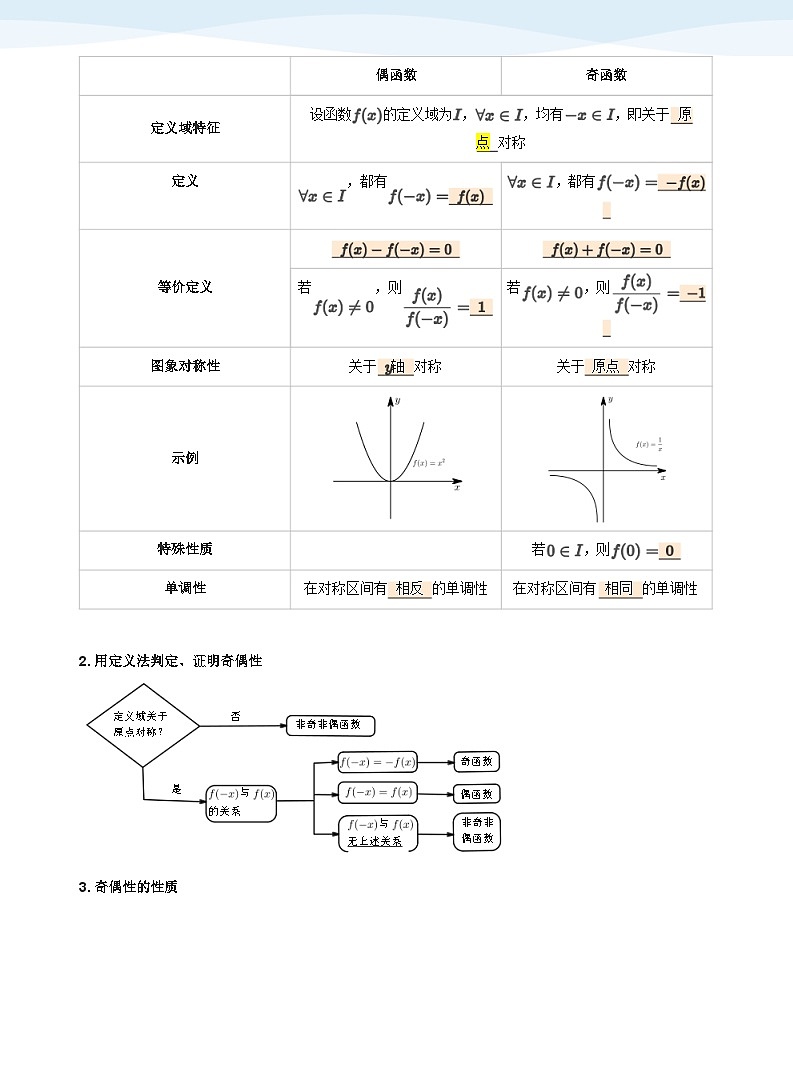
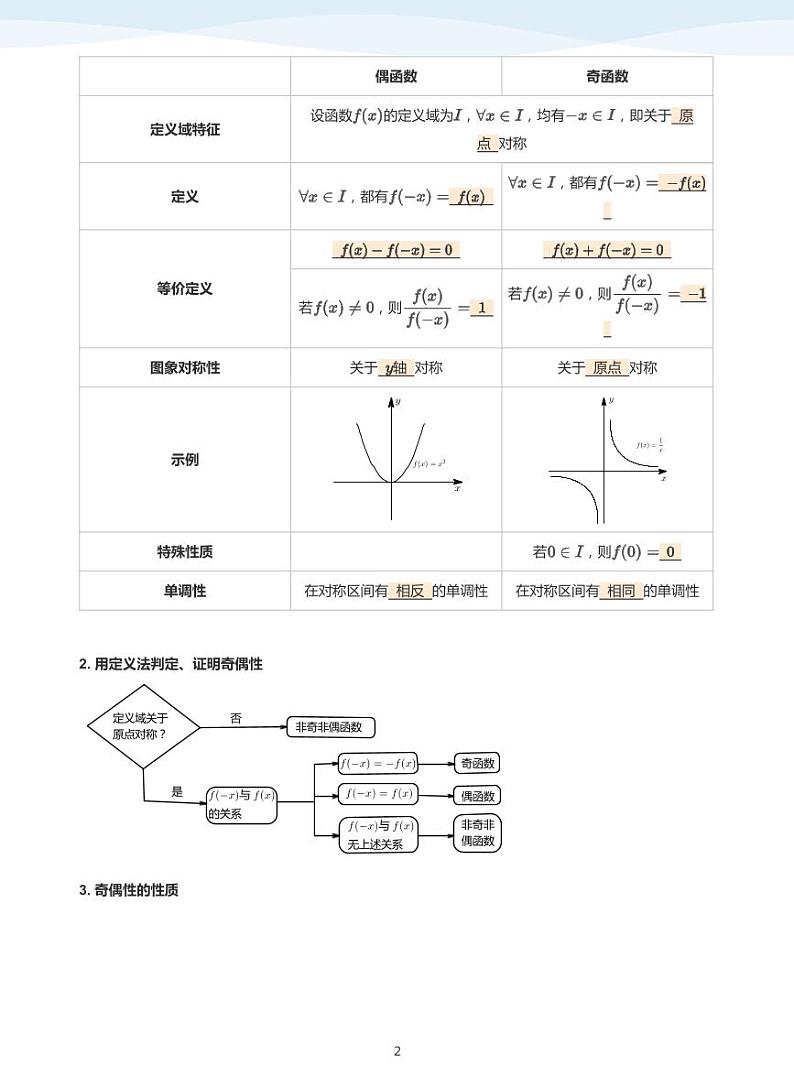
一、 奇偶性的定义、性质及判定
1. 奇偶性的定义
偶函数
奇函数
定义域特征
设函数
的定义域为 ,
,均有
对称
,即关于
定义,都有,都有
等价定义若,则若,则
图象对称性关于对称关于对称
示例
特殊性质
若
,则
单调性在对称区间有的单调性 在对称区间有的单调性
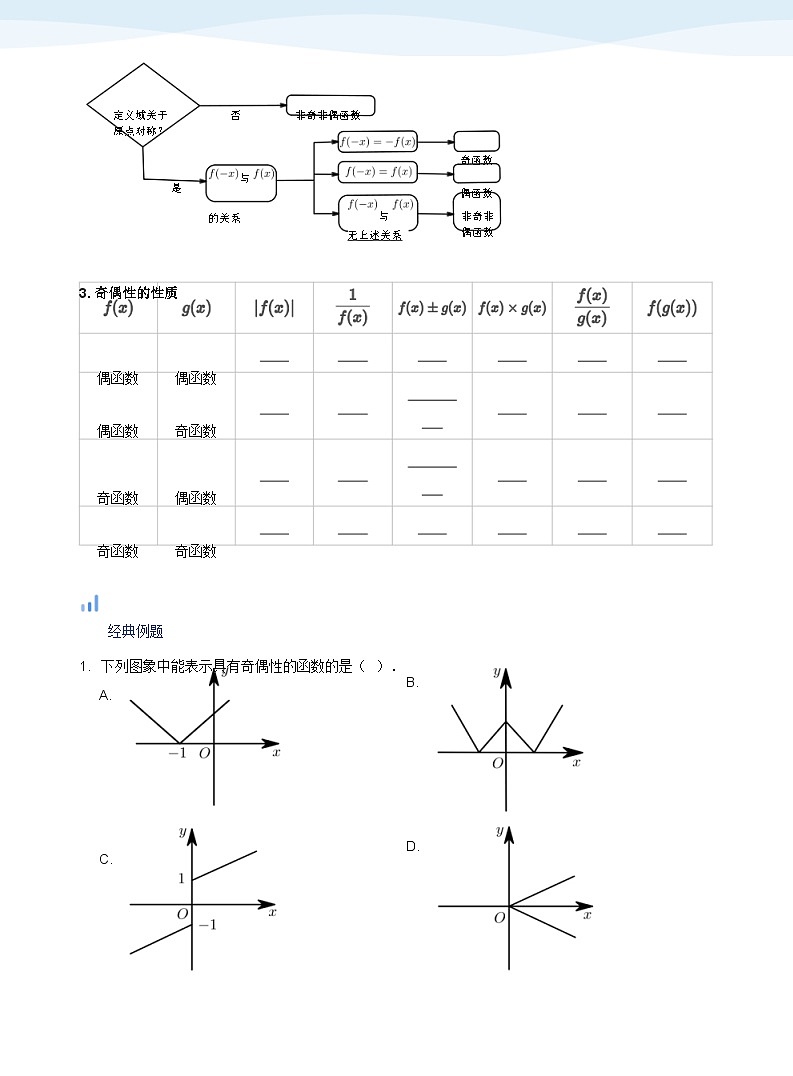
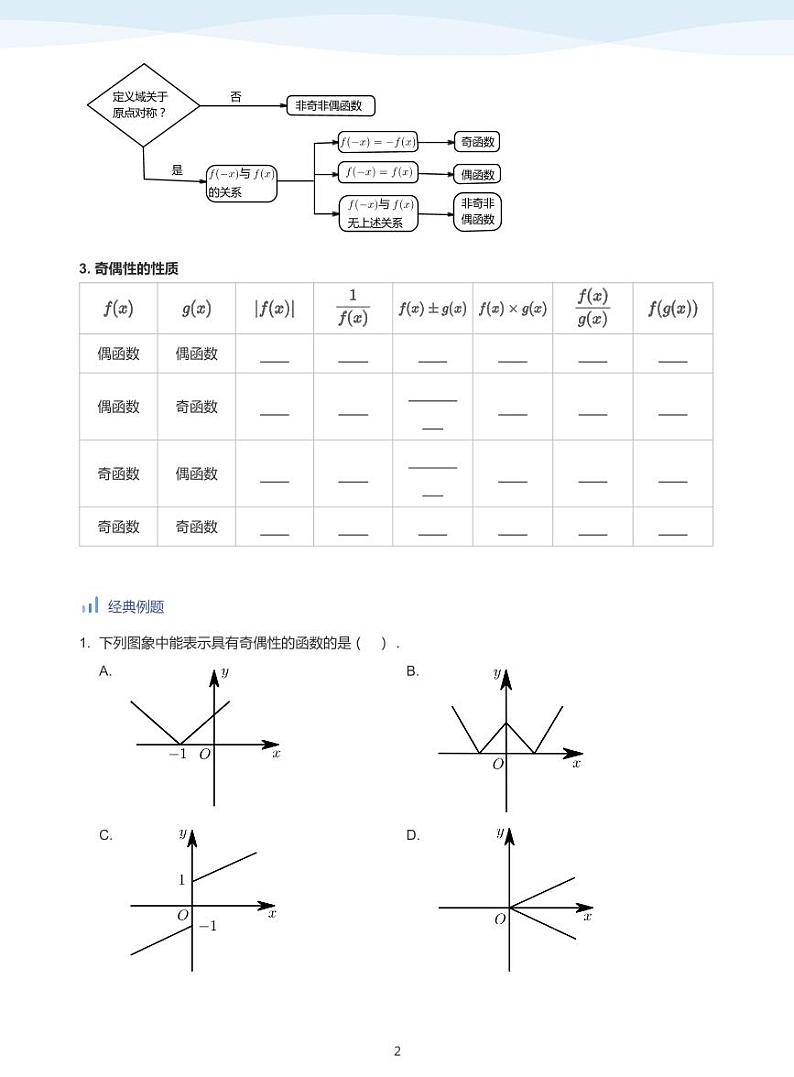
2. 用定义法判定、证明奇偶性
定义域关于
原点对称?
否
非奇非偶函数
是
与
奇函数
偶函数
的关系
与
无上述关系
非奇非
偶函数
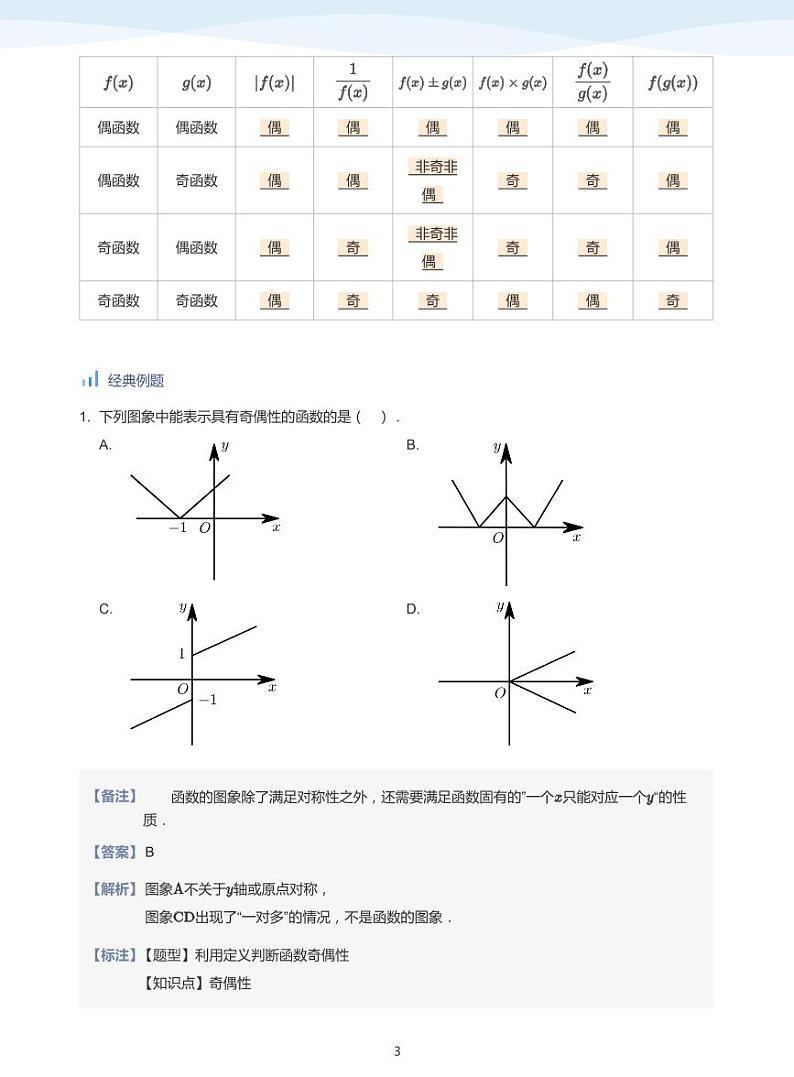
3. 奇偶性的性质
偶函数偶函数
偶函数奇函数
奇函数偶函数
奇函数奇函数
经典例题
1. 下列图象中能表示具有奇偶性的函数的是( ).
A.
C.
B.
D.
2. 解答下列各题:( 1 )设函数
和
分别是 上的偶函数和奇函数,则下列结论恒成立的是( ).
A.是偶函数B.是奇函数
C.是偶函数D.是奇函数
( 2 )设函数, 的定义域为 ,且是奇函数, 是偶函数,则下列结论中正确的是
( ).
A.是偶函数B.是奇函数
C.是奇函数D.是奇函数
巩固练习
3. 判断函数奇偶性
.
4. 函数的奇偶性是( ).
A. 奇函数B. 偶函数
C. 既不是奇函数也不是偶函数D. 既是奇函数也是偶函数
5. 判断下列函数的奇偶性.( 1 )
.
( 2 ).
( 3 ).
二、 奇偶性应用
1. 利用奇偶性求值
经典例题
6. 已知, 分别是定义在 上的偶函数和奇函数,且,则
( ).
A.B.C.D.
7. 已知,且,则.
8. 已知常数 ,,若函数,是偶函数,则.
巩固练习
9. 已知实数 , 满足,则.
10. 若函数为奇函数,则 =( ).
A.B.C.D.
11. 函数在区间上满足,则
的值为( ).
A.B.C.D.
12. 定义在
上的函数
满足:对任意 、
都有
.试求:
的值.
2. 利用奇偶性求解析式
经典例题
13. 已知函数是定义在 上的奇函数,当时,,则函数在 上的解析
式为.
14. 已知是定义在 上的偶函数, 是定义在 上的奇函数,且,求
, 的解析式.
巩固练习
15. 已知是定义在 上的偶函数,当时,,则函数在 上的解析式是(
).
A.B.C.D.
16. 已知为奇函数, 为偶函数,且,求、 .
3. 函数奇偶性与单调性、最值综合
1. 奇函数在对称区间上的单调性,若是奇函数,在区间上有最大(小)值
,则在区间上有最小(大)值.奇函数的最大值和最小值之和
为 ;
2. 偶函数在对称区间上的单调性
,若
是偶函数,在区间
上有最大(小)值
,则在区间上也有最大(小)值.
3. 单调性与奇偶性综合
①单调性解不等式的应用前一讲已经介绍过.例如,已知函数单调增,可将不等式转化
成.
②有一类题型,其形式为
,此类题目大概率是单调性与奇函数的综合应用.先移
其中一项,再利用奇函数将转化成,然后利用单调性求解.例如奇函数在 上单调增,欲
解不等式,先移项,再利用奇函数定义
,最后利用单调性,即.
③单调性与偶函数综合:例如偶函数在上单调增,欲解不等式,结合图象分析,
可知其等价于.
单调性与奇偶性的综合题目,一定要重视数形结合的运用!
经典例题
17. 已知函数,则下列结论正确的是( ).
A. B. C. D.
是偶函数,单调递增区间是是偶函数,单调递减区间是是奇函数,单调递减区间是是奇函数,单调递增区间是
18. 已知是定义在 上的偶函数,且在是增函数,设,,,
则 , , 的大小关系是( ).
A.B.C.D.
19. 函数在单调递减,且为奇函数.若,则满足的 的取
值范围是( ).
A.B.C.D.
20. 设奇函数在上是增函数,且,则不等式的解集为(
).
A.或B.或
C.或D.或
21. 若定义在上的函数满足:对任意 ,有
,且当时,有,设的最大值、最小值分别
为 , ,则的值为( ).
A.B.C.D.
22. 若关于 的函数的最大值为 ,最小值为 ,且
,则实数 的值为.
23. 定义在
( 1 )求
( 2 )若当
上的函数
的值.
时,有
满足:对任意的 ,
,求证:在
都有
上是单调递减函数.
.
( 3 )在( )的条件下解不等式:.
巩固练习
24. 设函数,则( ).
A. 是奇函数,且在上单调递增B. 是奇函数,且在上单调递减
C. 是偶函数,且在上单调递增D. 是偶函数,且在上单调递减
25. 已知是偶函数,是奇函数,它们的定义域均为,且它们在上的图
象如图所示,则不等式的解集是.
26. 已知函数在定义域 上单调递减,且函数的图象关于点对称.若实数 满足
,则的取值范围是( ).
A. B. C. D.
27. 已知为定义在 上的奇函数,,且对任意的 ,时,当
时,则不等式的解集为( ).
A.B.
C.D.
28. 已知,则在区间上的最大值和最小值之和等于( ).
A.B.C.D.
29. 已知函数.
( 1 )判断函数( 2 )试判断
( 3 )求函数
的奇偶性.
在区间
在区间
上的单调性,并用单调性定义证明.
上的最值.
30. 已知函数对任意实数 , 恒有,且当,,且
.
( 1 )判断
的奇偶性.
( 2 )求在区间
( 3 )解关于 的不等式
上的最大值.
.
导图总结
你学会了吗?快用思维导图来总结本节课所学吧!
出门练
31. 函数的部分图象如图所示,则( ).
A. B. C. D.
32. 已知函数和 均为奇函数,在区间上有最大值 ,那么
在上的最小值为( ).
A.B.C.D.
33. 已知是奇函数, 是偶函数,且,则( ).
A.B.C.D.
34. 已知函数的定义域是的一切实数,对定义域内的任意 , 都有
,且当时,.
( 1 )求证: 是偶函数.
( 2 )在上是增函数.
( 3 )解不等式.
8
人教A版 (2019)选择性必修 第二册5.1 导数的概念及其意义优质学案设计: 这是一份人教A版 (2019)选择性必修 第二册<a href="/sx/tb_c4000345_t4/?tag_id=42" target="_blank">5.1 导数的概念及其意义优质学案设计</a>,文件包含导数与函数的单调性极值与最值-讲义教师版docx、导数与函数的单调性极值与最值-讲义学生版docx等2份学案配套教学资源,其中学案共37页, 欢迎下载使用。
数学必修 第一册数学建模 建立函数模型解决实际问题学案: 这是一份数学必修 第一册<a href="/sx/tb_c4037448_t4/?tag_id=42" target="_blank">数学建模 建立函数模型解决实际问题学案</a>,文件包含函数的应用零点与函数模型-讲义教师版docx、函数的应用零点与函数模型-讲义学生版docx等2份学案配套教学资源,其中学案共47页, 欢迎下载使用。
数学3.3 幂函数学案设计: 这是一份数学<a href="/sx/tb_c4000269_t4/?tag_id=42" target="_blank">3.3 幂函数学案设计</a>,文件包含幂函数与对勾函数-讲义教师版docx、幂函数与对勾函数-讲义学生版docx等2份学案配套教学资源,其中学案共27页, 欢迎下载使用。














