北师大版七年级下册第二章 相交线与平行线3 平行线的性质课堂教学课件ppt

这是一份北师大版七年级下册第二章 相交线与平行线3 平行线的性质课堂教学课件ppt，共24页。PPT课件主要包含了“外行”的尴尬，判断就是命题，你能举出一些命题吗，回味无穷，已知事项，其它公理，“如果那么”，举反例等内容，欢迎下载使用。

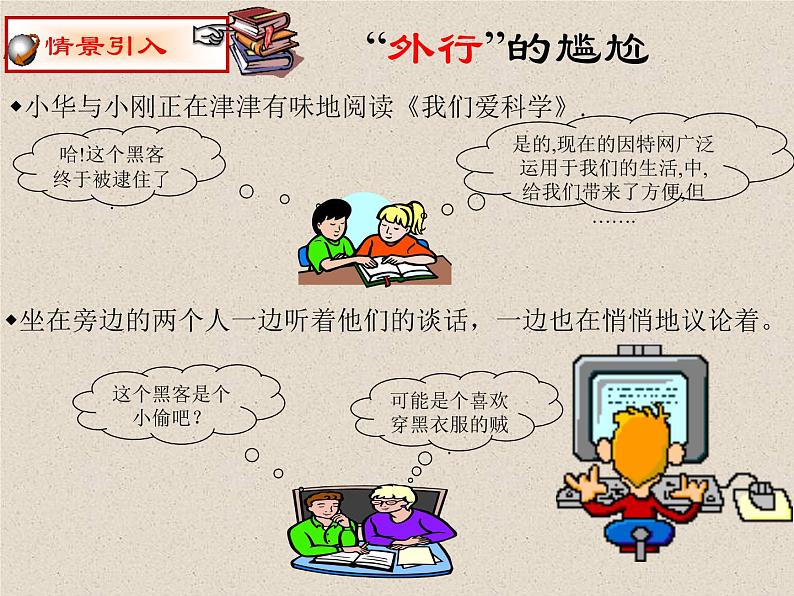
小华与小刚正在津津有味地阅读《我们爱科学》.
哈!这个黑客终于被逮住了.
是的,现在的因特网广泛运用于我们的生活,中,给我们带来了方便,但…….
坐在旁边的两个人一边听着他们的谈话，一边也在悄悄地议论着。
可能是个喜欢穿黑衣服的贼.
小明的百米成绩是9秒9.
继续努力,争取达到10秒.
有一位田径教练向领导汇报训练成绩
相传,阎锡山在观看士兵篮球赛,双方争抢非常激烈.于是命令:
发给每个人一个蓝球,不要再抢啦.
请同学们想一想，为什么会发生上述的笑话呢？
原因是因为我们在交流的时候，必须对某些名称和术语有共同的认识才能进行。为此，就要对名称和术语的含义加以描述，作出明确的规定，也就是给出它们的定义(definitin)。
例如: “具有中华人民共和国国籍的人,叫做中华人民共和国公民” 是“中华人民共和国公民”的定义;
“两点之间 线段的长度,叫做这两点之间的距离” 是“两点之间的距离”的定义;
“在一个方程中,只含有一个未知数,并且未知数的指数是1,这样的方程叫做一元一次方程” 是“一元一次方程”的定义;
“两组对边分别平行的四边形叫做平行四边形” 是“平行四边形”的定义;
你还能举出曾学过的“定义”吗?
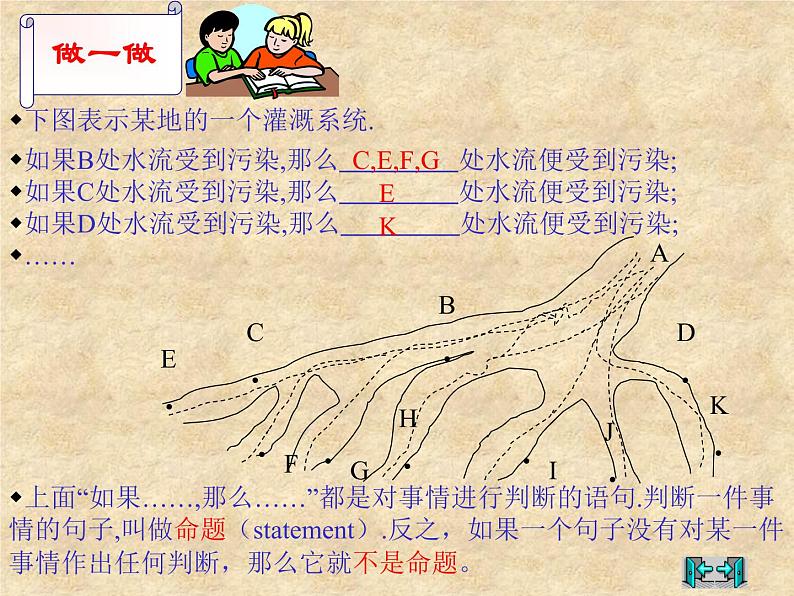
下图表示某地的一个灌溉系统.
上面“如果……,那么……”都是对事情进行判断的语句.判断一件事情的句子,叫做命题（statement）.反之，如果一个句子没有对某一件事情作出任何判断，那么它就不是命题。
如果B处水流受到污染,那么 处水流便受到污染;如果C处水流受到污染,那么 处水流便受到污染;如果D处水流受到污染,那么 处水流便受到污染;……
你能判断下列的句子哪些是命题？哪些不是命题吗？
（2）熊猫没有翅膀。
（3）你的作业做完了吗？
（4）任何一个三角形一定有直角。
（6）过直线l外一点作l的平行线。
（7）无论n为怎样的自然数，式子n2-n+11的值都是质数。
（8）如果两直线平行都和第三条直线平行，那么这两条直线也互相平行。
举出一些不是命题的语句.
你能说出一些正确的命题吗？你也能说出一些错误的命题吗？
定义:对名称和术语的含义加以描述,作出明确的规定,也就是给出它们的定义(definitin) . 定义是交流的基础.定义即具有确定含义的语句,它反映了事物最本质的意义.命题:判断一件事情的句子,叫做命题(statement).判断就是命题.命题可能正确,也可能错误. 不知你注意了没有,凡是命题,它的组成结构均有共同的特点,你能够总结出这个特点吗?
1。对于同一平面内的三条直线a，b，c，给出下列五个论断：①a∥b；② b∥c；③a⊥b；④a ∥c；⑤ a⊥c；⑥ b⊥c 。 使用其中三个论断，能组成一个你认为正确的命题和一个错误的命题吗？
2.在解决“何处水流受到污染”的问题中,找出几个命题.
定 义 与 命 题
炎陵县炎陵中学：罗艺军
1。你还记得什么叫做定义吗？命题呢？
2。你能判断下面的句子哪些是命题呢？
（2）三角形两边之和大于第三边；
（4）四边形都是菱形；
（6）有三个角是直角的四边形是矩形。
1、如果两个三角形的三条边对应相等，那么这两个三角形全等；2、如果一个四边形的一组对边平等且相等，那么这个四边形是平行四边形；3、如果一个三角形是等腰三角形，那么这个三角形的两个底角相等；4、如果一个四边形的对角线相等，那么这个四边形是矩形；5、如果一个四边形的两条对角线互相垂直，那么这个四边形是菱形。
下面的句子都是命题吗？这些命题有什么共同的结构待征？
如果一个三角形是等腰三角形，那么这个三 角形的两个底角相等。
由已知事项推断 出来的事项
命题都可以写成“如果……那么……”的形式；其中“如果”引出的部分是条件，“那么”引出的部分是结论。
1.下列命题的条件是什么?结论是什么?你能将它们改写成“如果。。。那么。。。”的`形式吗？
(1)如果两个角都是直角,那么它们不相等;
(2)如果a=b,b>c,那么a＜ c;
(3)两角和其中一角的对边对应相等的两个三角形全等;
(4)菱形的四条边都相等;
(5)全等三角形的面积相等.
2.上述的命题中,哪些是正确的?哪些是不正确的?你怎么知道它们是不正确的?与同伴交流.
正确的命题称为真命题(true statement),不正确的的命题称为假命题(false statement).
要说明一个命题是假命题,通常可以举出一个例子,使之具备命题的条件,而不具备命题的结论,这种例子称为反例(cunter example).
下面的几个命题，哪些是真命题的？哪些是假命题？你是怎么样知道它们是不正确的呢？
1。如果两个角相等，那么它们是对顶角。
2。如果a＞b，b＞c，那么a=c
3。垂直于同一直线的两直线平行。
4。互为相反数的两个数它们的绝对值相等。
你是用了什么方法来说明（1）和（2）是假命题的呢？
如何证实一个命题是真命题呢
用我们以前学过的观察,实验,验证特例等方法.
这些方法往往并不可靠.
能不能根据已经知道的真命题证实呢?
哪已经知道的真命题又是如何证实的?.
要说明一个命题是正确的，无论验证多少个特殊的例子，也无法保证命题的正确性，必须经过一步一步、有理有据地进行推理论证。
要说明一个命题是假命题，通常举出一个反例就可以了，反例是使之具有命题的条件，而不具有命题的结论。
了解数学知识发生与发展的历史
古希腊数学家 欧几里得(Eyclid,公元前300前后）
原名:某些数学名词称为原名.
公理:公认的真命题称为公理(axim).
证明:除了公理外,其它真命题的正确性都通过推理的方法证实.推理的过程称为证明.
定理:经过证明的真命题称为定理(therem).
本套教材选用如下命题作为公理 :1.两直线被第三条直线所截,如果同位角相等,那么这两条直线平行;2.两条平行线被第三条直线所截,同位角相等;3.两边夹角对应相等的两个三角形全等;4.两角及其夹边对应相等的两个三角形全等;5.三边对应相等的两个三角形全等;6.全等三角形的对应边相等,对应角相等.
等式的有关性质和不等式的有关性质都可以看作公理
在等式或不等式中,一个量可以用它的等量来代替.例如,如果,那么,这一性质也看作公理,称为“等量代换”.
1。命题的组成： 命题都是由条件和结论两部分组成
2。说明一个命题是假命题的方法：
3。说明一个命题是真命题的方法：
证明的依据：公理（等式的性质） 定义、已证明的定理
地理老师在黑板上画了一幅世界五大洲的图形，并给每个洲都写上了代号，然后，他请5个同学每人认出2个大洲，5个同学的回答是：甲：3号是欧洲，2号是美洲；乙：4号是亚洲，2号是大洋洲；丙：1号是亚洲，5号是非洲；丁：4号是非洲，3号是大洋洲；戊：2号是欧洲，5号是美洲。 地理老师说：“你们每个人都认对了一半。”请问，每个号码各代表什么洲呢？