初中数学北师大版七年级下册第二章 相交线与平行线3 平行线的性质精品ppt课件

这是一份初中数学北师大版七年级下册第二章 相交线与平行线3 平行线的性质精品ppt课件，文件包含231平行线的性质pptx、231平行线的性质教学设计docx等2份课件配套教学资源，其中PPT共20页， 欢迎下载使用。

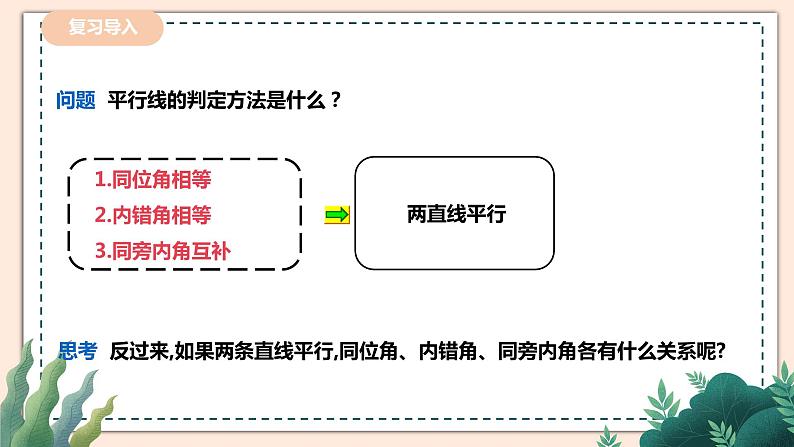
问题 平行线的判定方法是什么？
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
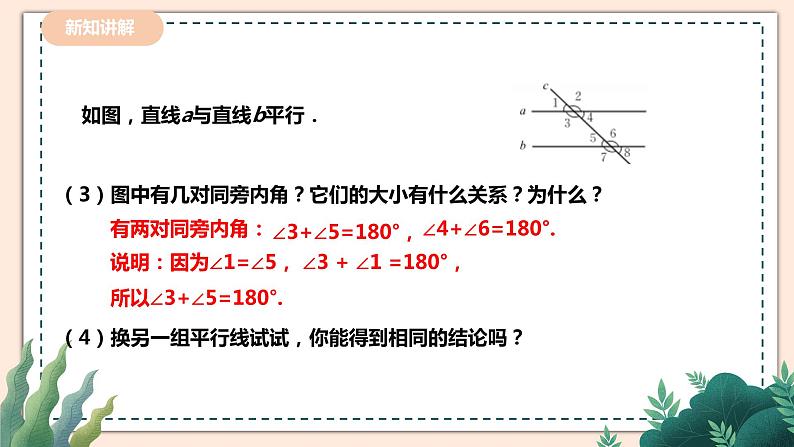
如图，直线a与直线b平行．
（1）测量同位角∠1和∠5的大小，它们有什么关系？图中还有其他同位角吗？它们的大小有什么关系？
由此猜想：两条平行线被第三条直线截得的同位角具有什么关系？
一般地，平行线具有如下性质：
性质1：两条平行线被第三条直线所截，同位角相等.简单说成：两直线平行，同位角相等.
所以∠1=∠2 （两直线平行，同位角相等）
（2）图中有几对内错角？它们的大小有什么关系？为什么？
因为∠3=∠7， ∠7=∠6,
同理： ∠4=∠5.
性质2：两条平行线被第三条直线所截，内错角相等.简单说成：两直线平行，内错角相等.
所以∠2=∠3. （两直线平行，内错角相等）
（3）图中有几对同旁内角？它们的大小有什么关系？为什么？（4）换另一组平行线试试，你能得到相同的结论吗？
∠3+∠5=180°，
∠4+∠6=180°.
说明：因为∠1=∠5， ∠3 + ∠1 =180°， 所以∠3+∠5=180°.
性质3：两条平行线被第三条直线所截，同旁内角互补.简单说成：两直线平行，同旁内角互补.
所以∠2+∠4=180 °（两直线平行，同旁内角互补）
如图所示，AB//CD, AC//BD. 分别找出与∠1相等或互补的角.
平行线三个性质的条件是什么？结论是什么？它与判定有什么区别？
如图，一束平行光线AB与DE射向一个水平镜面后被反射，此时∠1=∠2，∠3=∠4. （1）∠1与∠3的大小有什么关系？ （2）反射光线BC与EF也平行吗？
你能说明每一步的理由吗?你是如何思考的？ 与同伴进行交流。
光线在不同介质中的传播速度是不同的，因此当光线从水中射向空气时，要发生折射，由于折射率相同，所以在水中平行的光线，在空气中也是平行的.如图，∠1＝45°，∠2＝122°，求图中其他角的度数.
解：由题意得：∠3 =∠1 = 45°，∠1+∠7 = 180°，∴∠7 = 180°－∠1 = 135°.∴∠8 =∠7 = 135°.又∠4 =∠2 = 122°，∠2 +∠5 = 180°，∴∠5 = 180°－∠2 = 58°.∴∠6=∠5=58°.
1. 如图，AB∥EF，CD⊥EF，∠BAC=50°，则∠ACD等于(　　)A. 120° B. 130° C. 140° D. 150°2. 如图，直线a∥b，直线c与直线a，b相交，若∠1=56°，则∠2等于(　　)A. 24° B. 34° C. 56° D. 124°
3. 如图，∠AOB=40°，OP平分∠AOB，点C为射线OP上一点，作CD⊥OA于点D，在∠POB的内部作CE∥OB，则∠DCE=____________.4.如图，AB∥CD，∠A=50°，∠C=30°，则∠AEC等于 .
5. 如图，点A，B，C，D在一条直线上，CE与BF交于点G，∠E=∠F，CE∥DF，试说明∠A=∠1．
解：因为CE∥DF，所以∠F=∠2.因为∠E=∠F，所以∠E=∠2.所以AE∥BF.所以∠A=∠1（两直线平行，同位角相等）．
6. 如图，已知AB∥CD，BC平分∠ABE，∠C=32°，求∠BED的度数.
解：因为AB∥CD，所以∠ABC=∠C=32°. 又因为BC平分∠ABE，所以∠ABC=∠EBC=32°. 所以∠BED=∠ABE=∠ABC+∠EBC=64°.
同位角相等内错角相等同旁内角互补
1.课本第51页习题2.5第1、2、3题