资料中包含下列文件,点击文件名可预览资料内容





当前文件暂不支持在线预览,请下载使用
还剩20页未读,
继续阅读
成套系列资料,整套一键下载
北师大版数学七年级下册 2.3.1《平行线的性质》第1课时 课件+分层练习(含答案解析)
展开
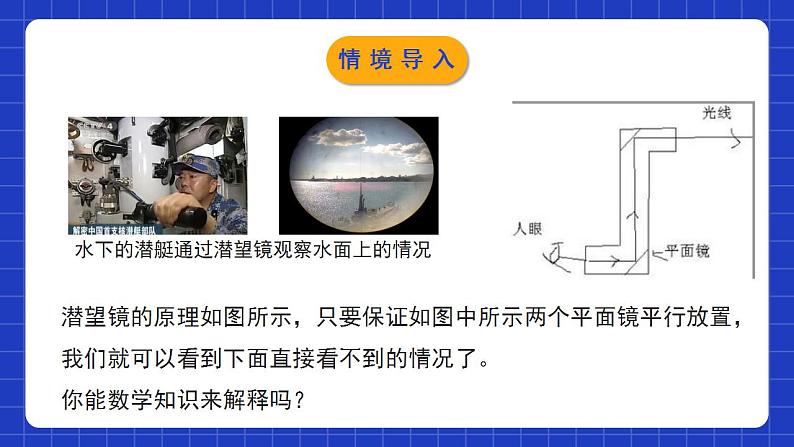
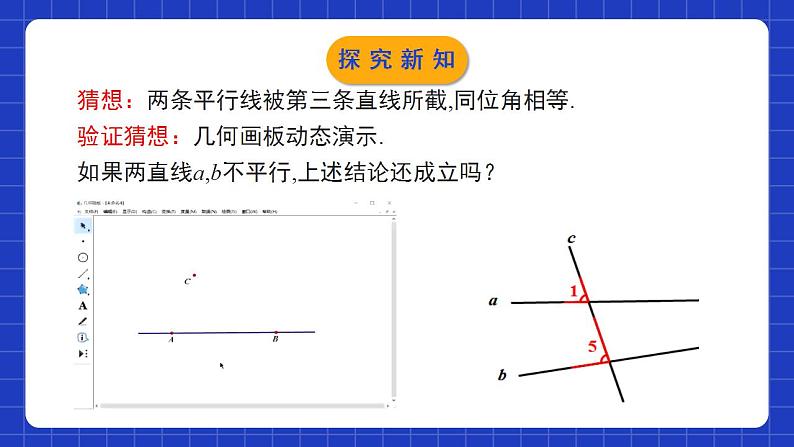
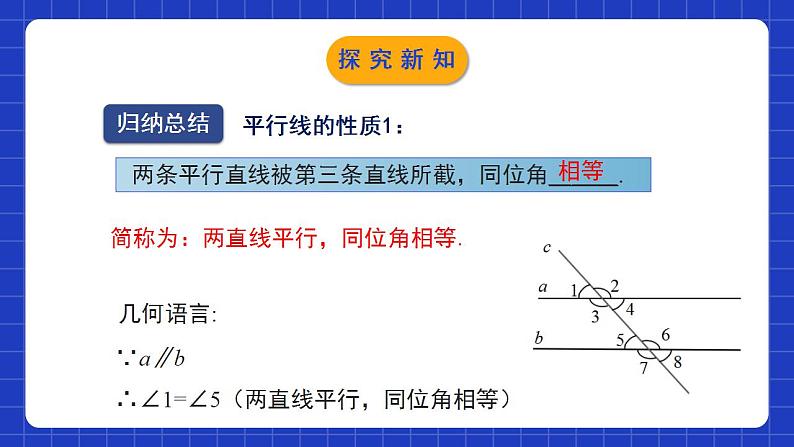
2.3.1平行线的性质第1课时学习目标1经历探索平行线性质的过程,掌握平行线的三条性质,并能使用文字语言或者符号语言进行简单的推理论证.2经历观察、测量、猜想与验证的过程,培养动手操作能力,发展空间观念、数学推理与符号感.3在活动中体验探索、交流、成功与提升的喜悦,激发学习数学的兴趣,培养勇于实践,大胆猜测、推理的科学态度.如果同位角相等,那么这两条直线平行。平行线的判定方法:如果同旁同角互补,那么这两条直线平行。如果内错角相等,那么这两条直线平行。情境导入水下的潜艇通过潜望镜观察水面上的情况潜望镜的原理如图所示,只要保证如图中所示两个平面镜平行放置,我们就可以看到下面直接看不到的情况了。你能数学知识来解释吗?情境导入平行线的性质如图,直线a与直线b平行. 测量同位角∠1和∠5的大小,它们有什么关系?图中还有其他同位角吗?它们的大小有什么关系?相等:∠1=∠5,∠2=∠6,∠3=∠7,∠4=∠8 .探究新知猜想:两条平行线被第三条直线所截,同位角相等.验证猜想:几何画板动态演示.如果两直线a,b不平行,上述结论还成立吗?探究新知归纳总结 两条平行直线被第三条直线所截,同位角___.相等简称为:两直线平行,同位角相等.∴∠1=∠5(两直线平行,同位角相等) ∵a∥b几何语言:平行线的性质1:探究新知 图中有几对内错角?它们的大小有什么关系?为什么?有两对内错角:∠3=∠6、∠4=∠5;因为∠3=∠7, ∠7= ∠6, 同理: ∠4=∠5. 所以∠3=∠6.说明:如图,直线a与直线b平行.探究新知归纳总结平行线的性质2:两条平行直线被第三条直线所截,内错角 . ∴∠4=∠5(两直线平行,内错角相等)几何语言:简称为:两直线平行,内错角相等. ∵a∥b相等探究新知有两对同旁内角:∠3+∠5=180°,∠4+∠6=180°.说明:因为∠1=∠5, ∠3 + ∠1 =180°, 所以∠3+∠5=180°.如图,直线a与直线b平行. 图中有几对同旁内角?它们的大小有什么关系?为什么?探究新知归纳总结平行线的性质3:两条平行直线被第三条直线所截,同旁内角 . ∴∠3+∠5=180 °(两直线平行,同旁内角互补)∵a∥b几何语言:互补简称为:两直线平行,同旁内角互补. 探究新知同位角相等内错角相等同旁内角互补两直线平行条件性质归纳总结探究新知(1)解题时经常会综合应用平行线的性质与条件,通常有两种形式: ①由平行关系→角的相等或互补→直线平行; ②由角的相等或互补→直线平行→新的角的相等或互补.有时也会反复利用平行线的性质与条件,得出最终结果.要熟练掌握它们之间的关系(2)利用平行线的条件与性质解题时,关键是要看清题目中的平行关系是否作为已知条件给出,从而选择适当的方法来解题。探究新知例:如图,一束平行光线 AB 与DE 射向一个水平镜面后被反射,此时∠1 =∠2,∠3 =∠4.(1)∠1 与∠3的大小有什么关系?∠2与∠4 呢?(2)反射光线BC与EF也平行吗?探究新知解(1)∠1=∠3,∠2=∠4
∵AB//DE(平行光线)∴∠1=∠3(两直线平行,同位角相等)而∠1 =∠2,∠3 =∠4 ∴ ∠2=∠4
(2)平行
∵∠2=∠4 ∴ BC//EF(同位角相等,两直线平行)
探究新知1. 如图,若AB∥CD,则下列结论一定成立的是( )A.∠1=∠2B. AD∥BCC. ∠B=∠DD. ∠3=∠4D随堂练习2.如图,已知a∥b,小华把三角板的直角顶点放在直线a上.若∠1=40°,则∠2的度数为( )A.100°B. 110°C. 120°D. 130°D随堂练习3.如图,已知CD∥BE,∠1=68°,那么∠B的度数为( )A. 68° B. 102°C. 110° D. 112°D随堂练习4. 如图,用一吸管吮易拉罐内的饮料时,吸管与易拉罐上部夹角∠1=74°,那么吸管与易拉罐下部夹角∠2=________.74°随堂练习5.如图,直线l1∥l2∥l3,点A、B、C分别在直线l1、l2、l3上,若∠1=70°,∠2=50°,则∠ABC=________.120°随堂练习6.如图,直线l1∥l2,∠1=20°,则∠2+∠3=________.200°随堂练习7.如图,AB∥CD,∠α=45°,∠D=∠C,依次求出∠D,∠C,∠B的度数.解:∵AB∥CD,∠α=45°∴∠D=∠α=45°又∵∠D=∠C,∴∠C=45°∵DC∥AB∴∠C+∠B=180°∴∠B=180°-∠C=180°-45°=135°随堂练习8.如图,AC∥ED,AB∥FD,∠A=64°,求∠EDF的度数.解:∵AC∥ED∴∠EDF=∠CFD∵AB∥FD∴∠CFD=∠A∴∠EDF=∠A=64°随堂练习9.如图,AB∥CD,点E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE的度数.随堂练习10. 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,求∠1的度数. 随堂练习随堂练习角的数量关系直线的位置关系(决定)平行线的判定角的数量关系直线的位置关系平行线的性质(得到)同位角相等内错角相等同旁内角互补两直线平行课堂小结课程结束
相关资料
更多









