初中数学北师大版七年级下册4 整式的乘法评课课件ppt

这是一份初中数学北师大版七年级下册4 整式的乘法评课课件ppt，共20页。PPT课件主要包含了学习目标，导入新课，新知探究，+an，+bm，+bn，典例精析，当堂练习，课堂小结等内容，欢迎下载使用。
1.理解并掌握多项式与多项式的乘法运算法则.（重点）2.能够用多项式与多项式的乘法运算法则进行计算.（难点）
2.单项式乘多项式:单项式与多项式相乘,就是根据分配律用单项式去乘　　　　　　　　,再把所得的　　　相加. 
1.单项式乘单项式:单项式与单项式相乘,把它们的　　　 、 　　 分别相乘,其余字母连同它的指数不变,作为积的　 . 
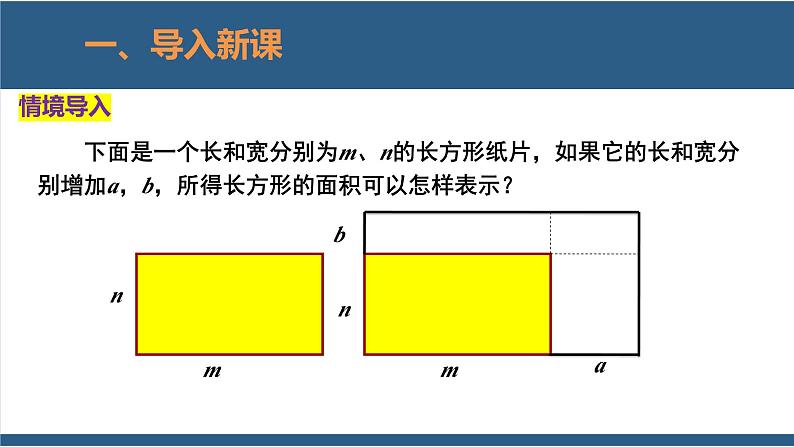
下面是一个长和宽分别为m、n的长方形纸片，如果它的长和宽分别增加a，b，所得长方形的面积可以怎样表示？
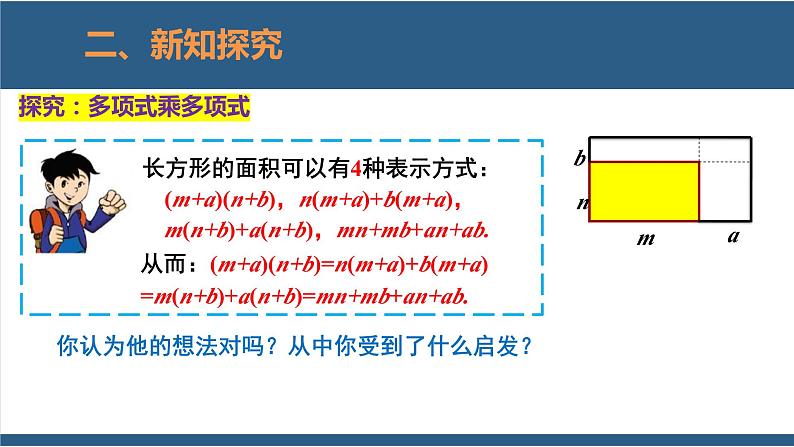
从而：(m+a)(n+b)=n(m+a)+b(m+a)=m(n+b)+a(n+b)=mn+mb+an+ab.
你认为他的想法对吗？从中你受到了什么启发？
议一议：你是用什么方法计算上面的问题的？如何进行多项式与多项式相乘的运算？
多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加.
1.计算:（1）(1－x)(0.6－x)； (2)(2x+y)(x－y)；
解： (1) 原式=1×0.6－1×x－x·0.6+x·x =0.6－x－0.6x+x2 =0.6－1.6x+x2；
(2) 原式=2x·x－2x·y+y·x－y·y =2x2－2xy+xy－y2 =2x2－xy－y2；
两项相乘时,先定符号,最后的结果要合并同类项.
解：原式=x·x2－x·xy+xy2+x2y－xy2+y·y2 =x3－x2y+xy2+x2y－xy2+y3 = x3+y3.
(3) (x+y)(x2－xy+y2).
注意:(1)不要漏乘;(2)注意符号问题;(3)最后结果应化成最简形式（是同类项的要合并）.
2.先化简，再求值：(a－2b)(a2＋2ab＋4b2)－a(a－5b)(a＋3b)，其中a＝－1，b＝1.
解：原式＝a3－8b3－(a2－5ab)(a＋3b)＝a3－8b3－a3－3a2b＋5a2b＋15ab2＝－8b3＋2a2b＋15ab2.当a＝－1，b＝1时，原式＝－8＋2－15＝－21.
例1 计算:(1)(-2m-1)(3m-2);(2)(x-y)2.
解:(1)原式=-2m·3m-2m·(-2)-1·3m-1×(-2) =-6m2+4m-3m+2 =-6m2+m+2.
(2)原式=(x-y)(x-y) =x2-xy-xy+y2 =x2-2xy+y2.
例2：若(x-2)(x2+ax+b)的积中不含x的二次项和一次项,则a,b的值分别是多少?
解:(x-2)(x2+ax+b)=x3+ax2+bx-2x2-2ax-2b=x3+(a-2)x2+(b-2a)x-2b.因为(x-2)(x2+ax+b)的积中不含x的二次项和一次项,所以a-2=0,b-2a=0,解得a=2,b=4.
1.计算(a-2)(a+3)的结果是(　　)A.a2-6B.a2+a-6C.a2+6D.a2-a+6
2.下列各式中,错误的是(　　)A.(x+1)(x+2)=x2+3x+2B.(x-4)(x+4)=x2-16C.(2x+3)(2x-6)=2x2-3x-18D.(2x-1)(2x+2)=4x2+2x-2
4.设M=(x-3)(x-7),N=(x-2)(x-8),则M,N的大小关系为(　　)A.M>N B.M=N C.M