北师大版七年级下册4 整式的乘法图片ppt课件

这是一份北师大版七年级下册4 整式的乘法图片ppt课件，共19页。PPT课件主要包含了多项式乘多项式，a²b·2ab3，c2·m＋n－p，c²·m，+c²·n，-c²p，manb，mnb，anb，单项式乘多项式等内容，欢迎下载使用。

1.熟练掌握多项式乘多项式的运算法则.2.能够熟练地进行多项式与多项式的乘法计算，发展运算能力. 3.经历探索多项式乘多项式的运算法则的过程，通过类比学习，利用乘法的运算律将问题转化，培养学生转化的数学思想.4.让学生主动参与到探索过程中，培养学生思维的严密性和初步解决问题的能力.
准备好了吗？一起去探索吧！
=(3×2)(a2·a)(b·b3)= 6a3b4
=c²m+c²n-c²p
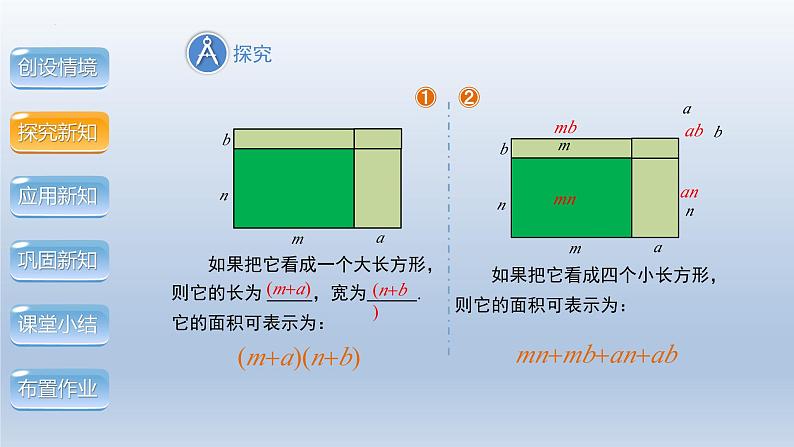
如图1是一个长和宽分别为m，n的长方形纸片，如果它的长和宽分别增加a，b，所得的长方形(图2)的面积可以怎样表示呢?
如果把它看成四个小长方形，则它的面积可表示为：
mnmbanab
如果把它看成一个大长方形，则它的长为 ，宽为 .它的面积可表示为：
如果把它看成上下两个大长方形，则它的面积可表示为：
n(ma)b(ma)
如果把它看成左右两个大长方形，则它的面积可表示为：
m(nb)a(nb)
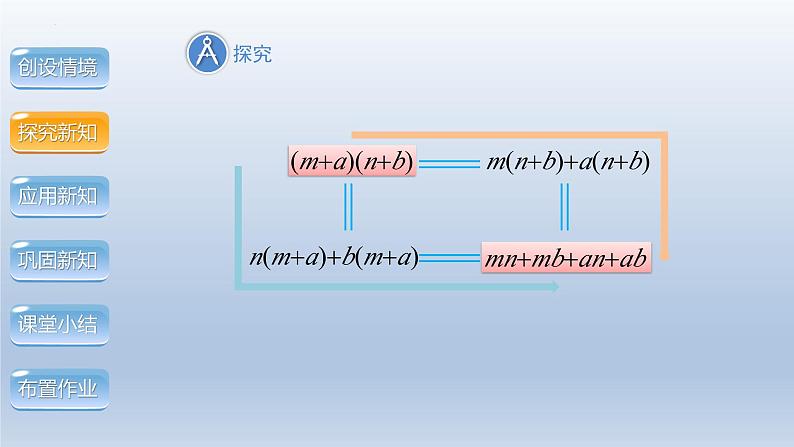
由此你得到了什么启发?
mnmbanab
你是用什么方法计算上面的问题的？
多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加.
计算： (1) (1x)(0.6x)； (2) (2x+y)(xy)；
(1) (1x)(0.6x) =1×0.61×xx×0.6x·x =0.6x0.6xx2 =0.61.6xx2.(2) (2x+y)(xy) =2x·x2x·y+y·x  y·y =2x22xy+xyy2 =2x2xyy2
多项式乘以多项式时，应注意以下几点：(1)相乘时，按一定的顺序进行，必须做到不重不漏；(2)多项式与多项式相乘，仍得多项式，在合并同类项之前，积的项数应等于原多项式的项数之积；(3)相乘后，若有同类项应该合并．
1.计算： (1) (m+2n)(m-2n)； (2)(2n+5)(n-3)； (3) (x+2y)²； (4) (2x+b)(3x+d) .
解：原式m2-2mn+2mn-4n2m2-4n2
解：原式2n2-6n+5n-152n2-n-15
解：原式6x2+2xd+3xb+bd
解：原式(x+2y)(x+2y)x2+2xy+2xy+4y2x2+4xy+4y2
3.先化简，再求值： (x1)(x²x+1)+(x2)(x²+2x+4)，其中x .
解： (x1)(x²x+1)+(x2)(x²+2x+4)  x3x²+x+x²x+1+x3+2x²+4x2x²4x8 2x37
多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加.
(1)相乘时，按一定的顺序进行，必须做到不重不漏；(2)多项式与多项式相乘，仍得多项式，在合并同类项之前，积的项数应等于原多项式的项数之积；(3)相乘后，若有同类项应该合并．
教科书 第19页习题1.8 第1、2题