












初中数学北师大版七年级下册4 整式的乘法试讲课备课ppt课件
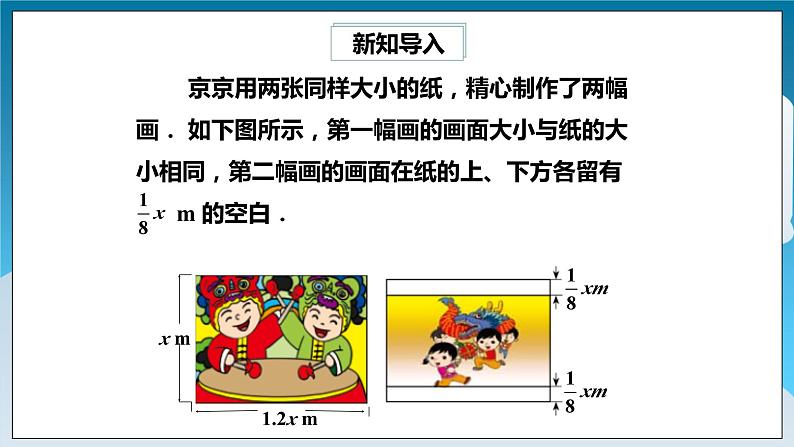
展开京京用两张同样大小的纸,精心制作了两幅画. 如下图所示,第一幅画的画面大小与纸的大小相同,第二幅画的画面在纸的上、下方各留有 m 的空白.
(1)第一幅画的画面面积是多少平方米?第二幅呢?你是怎样做的?(2)若把图中的 1.2 x 改为 mx,其他不变,则两幅画的面积又该怎样表示呢?
第一幅画的画面面积是x·1.2x 平方米第二幅画的画面面积是 平方米
第一幅画的画面面积是x·mx平方米第二幅画的画面面积是 平方米
想一想:问题1:对于以上求面积时,所遇到的是什么运算?问题2:什么是单项式?
因为因式是单项式,所以它们相乘是单项式乘以单项式运算.
表示数与字母的积的代数式叫做单项式.
对于上面的问题的结果:
这两个结果可以表达得更简单些吗?说说你的理由?
第一幅画的画面面积是 米2 ,
第二幅画的画面面积是 米2 .
根据乘法的交换律、结合律,幂的运算性质.
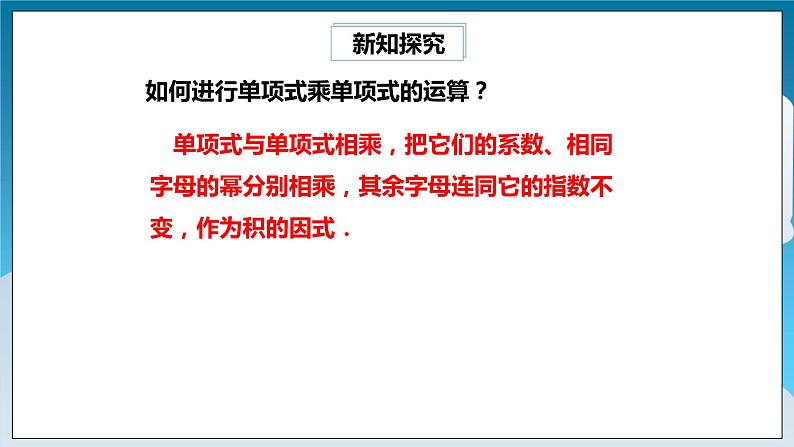
如何进行单项式乘单项式的运算?
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式.
例1 计算:(1) ; (2) - 2 a2b3 · ( - 3a) ;(3) 7 xy 2z·(2xyz) 2.
解:(1) ;(2)- 2 a2b3·( - 3a) = [ ( - 2)·( - 3) ] ( a2 a)·b3 = 6 a3b3 ;(3)7 xy 2z·(2xyz) 2=7xy2z ·4x2y2z2= 28x3y4z3 ;
问题1:ab·(abc+2x) 和c2·(m+n-p)等于什么?你是怎样计算的?
ab·(abc+2x)=ab·abc+ab·2x=a2b2c+2abxc2·(m+n-p)=c2·m+c2·n-c2·p=mc2+nc2-pc2
单项式与多项式相乘时,分两个阶段:
①按分配律把单项式与多项式的乘积写成单项式与单项式乘积的代数和的形式;
单项式与多项式相乘的法则:单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加.
例2:计算:(1) 2ab (5ab2+3a2b ) ; (2) ; (3) 5 m2n (2n+3m-n2 ) ; (4) 2 ( x+y2z+xy2z3 )·xyz.
解:(1) 2ab (5ab2+3a2b ) =2ab·5 ab2+2ab·3a2b =10a2b3+ 6a3b2; (2) (3) 5 m2n (2n+3m-n2 ) =5m2n·2n+5m2n·3m +5m2n· ( -n2) =10m2n2+15m3n - 5m2n3;
解:(4)2 ( x+y2z+xy2z3 )·xyz = (2x +2y2z+2xy2z3) ·xyz =2x·xyz+2y2z·xyz+2xy2z3·xyz =2x2yz+2xy3z2+2x2y3z4 .
图1-1是一个长和宽分别为 m,n的长方形纸片,如果它的长和宽分别增加 a,b,所得长方形(图 1-2)的面积可以怎样表示?
小明的想法:长方形的面积可以有 4 种表示方式:( m+a ) (n+b ),n(m+a) +b(m+a),m(n+b) + a(n+ b) 和mn+mb+na+ba,从而,(m+a) (n+b) = n(m +a) + b(m+a) =m (n+b)+a (n+b) =mn+mb+na+ba.你认为小明的想法对吗?从中你受到了什么启发?
把 (m+a) 或 (n+b) 看成一个整体,利用乘法分配律,可以得到 (m+a) (n+b) = (m+a)n+ (m+a)b =mn+an+mb+ab,或 ( m+a) (n+b)=m(n+b)+a( n+b) = mn+mb+an+ab.
如何进行多项式与多项式相乘的运算?
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
例3 计算:(1)( 1 - x ) ( 0.6 - x ) ; (2)( 2 x + y ) ( x - y ) .
解:(1)( 1 - x ) ( 0.6 - x ) =1×0.6 - 1×x - x ×0.6 +x ×x= 0.6 - 1.6 x + x 2 ; (2)( 2 x + y ) ( x - y ) = 2x·x-2x·y+y·x -y·y=2x2-2 xy+xy-y2=2x2 -xy-y2 .
1.计算:(1)( m+2n ) ( m - 2n );(2)( 2n+5 ) ( n-3);(3)( x+ 2y ) 2 ; (4)( ax+b) ( cx+d).
解:(1)( m+2n ) ( m - 2n )= m·m-m·2n + 2n·m - 2n·2n =m2-2mn + 2mn - 4n2=m2- 4n2; (2)( 2n+5 ) ( n-3)= 2n·n-2n·3+5·n-5×3 = 2n2-6n+5n-15= 2n2-n-15;(3)( x+2y ) 2 =( x+2y ) ( x+2y ) =x2+x·2y +x·2y+ 2y·2y=x2+4xy + 4y2; (4)( ax+b) ( cx+d)= ax·cx+ax·d+b·cx+b·d =ac x2+adx+bcx+bd.
1、先用一个多项式的第一项遍成另一个多项式的各项,再用这个多项式的第二项遍乘另一个多项式的各项,依次类推,并把所得的积相加;
多项式与多项式相乘,可分几个步骤进行?
通过本节课的内容,你有哪些收获?
1.单项式与单项式相乘的运算:
2.单项式与多项式相乘的运算:
3.多项式与多项式相乘的运算:
人教统编版高中语文选择性必修上册
教习网(以下简称“本网站”)系属深圳市智学帮科技有限公司(以下简称“本公司”)旗下网站,为维护本公司合法权益,现依据相关法律法规作出如下郑重声明:1.本文件仅用于个人学习、研究,不得用于商业性或盈利性用途,不得侵犯本司及相关权利人的合法权利。一旦发现侵权,本公司将联合司法机关获取相关用户信息并要求侵权者承担相关法律责任。2.本网站上所有原创内容,是本公司依据相关法律法规,安排专项经费运营规划,组织老师创作完成,著作权归属本公司所有。3.经由网站用户上传至本网站的课件、教案、学案、试卷等内容,其作品仅代表作者本人观点,本网站不保证其内容的有效性,凡因本作品引发的任何法律纠纷,均由上传用户承担法律责任,本网站仅有义务协助司法机关了解事实情况。
教习网()专为 K12教育老师提供同步备课资料下载、教学经验学习等服务的互联网教育平台。为了进一步完善网站的资料体系,最大化满足用户的精品资源需求,现诚邀全国各地优秀一线老师加入教习网兼职创作老师团队,参与资源建设,获取高额现金收益。兼职招募详情请看:
教习网诚挚地为各位老师推荐两款免费的朗读小程序,可用于课前预习、课中学习和课后复习,打开微信扫下方二维码即可使用,欢迎分享广大师生使用。
初中北师大版2 频率的稳定性精品备课课件ppt: 这是一份初中北师大版<a href="/sx/tb_c77854_t3/?tag_id=26" target="_blank">2 频率的稳定性精品备课课件ppt</a>,文件包含622《抛硬币试验》课件pptx、622《抛硬币试验》教案doc、622《抛硬币试验》练习doc、622《抛硬币试验》学案doc等4份课件配套教学资源,其中PPT共30页, 欢迎下载使用。
初中数学北师大版七年级下册2 频率的稳定性评优课备课ppt课件: 这是一份初中数学北师大版七年级下册<a href="/sx/tb_c77854_t3/?tag_id=26" target="_blank">2 频率的稳定性评优课备课ppt课件</a>,文件包含621《抛图钉试验》课件pptx、621《抛图钉试验》教案doc、621《抛图钉试验》练习doc、621《抛图钉试验》学案doc等4份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
初中数学北师大版七年级下册2 图形的全等优秀备课ppt课件: 这是一份初中数学北师大版七年级下册<a href="/sx/tb_c9987_t3/?tag_id=26" target="_blank">2 图形的全等优秀备课ppt课件</a>,文件包含42《图形的全等》课件pptx、42《图形的全等》教案doc、42《图形的全等》练习doc、42《图形的全等》学案doc等4份课件配套教学资源,其中PPT共21页, 欢迎下载使用。