2024九年级数学下册第5章二次函数5.5用二次函数解决问题3营销中的最值习题课件新版苏科版

这是一份2024九年级数学下册第5章二次函数5.5用二次函数解决问题3营销中的最值习题课件新版苏科版，共49页。

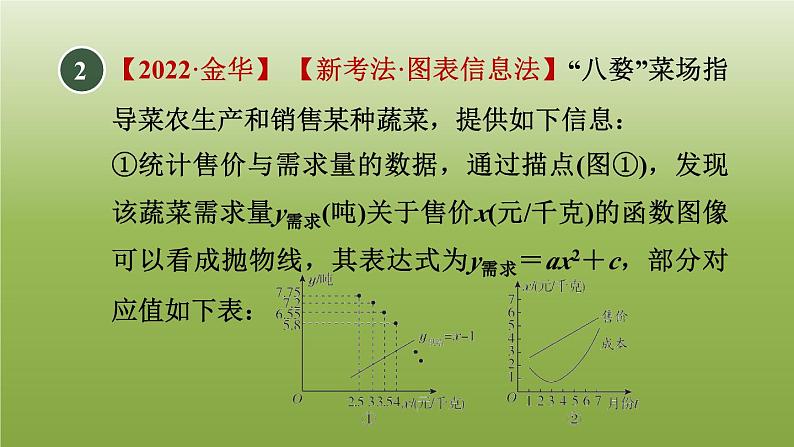
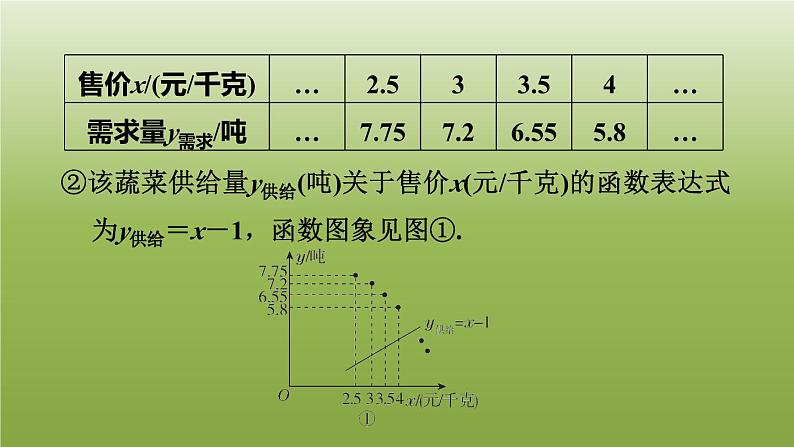
用二次函数解决问题营销中的最值5.5.3 1 (1)m＝________，n＝________；－260　【点拨】(2)求第x天的销售额W(元)与x之间的函数关系式；解：在W＝－2x2＋40x＋600中，令W＝1 000，得－2x2＋40x＋600＝1 000，整理得x2－20x＋200＝0，方程无实数解；(3)在试销售的30天中，销售额超过1 000元的共有多少天？2【2022·金华】 【新考法·图表信息法】“八婺”菜场指导菜农生产和销售某种蔬菜，提供如下信息：①统计售价与需求量的数据，通过描点(图①)，发现该蔬菜需求量y需求(吨)关于售价x(元/千克)的函数图像可以看成抛物线，其表达式为y需求＝ax2＋c，部分对应值如下表：②该蔬菜供给量y供给(吨)关于售价x(元/千克)的函数表达式为y供给＝x－1，函数图象见图①.请解答下列问题：(1)求a，c的值．【点方法】利用待定系数法求解即可；· · · · · (2)根据图②，哪个月出售这种蔬菜每千克获利最大？并说明理由．【点方法】设每个月销售这种蔬菜每千克获利w元，根据w＝x售价－x成本列出函数表达式，化成顶点式求解； (3)求该蔬菜供给量与需求量相等时的售价，以及按此价格出售获得的总利润．【点方法】根据题意列出方程，求出x的值，再求总利润即可．3【2023·营口】 【情境题·商业应用】某大型超市购进一款热销的消毒洗衣液，由于原材料价格上涨，今年每瓶洗衣液的进价比去年每瓶洗衣液的进价上涨4元，今年用1 440元购进这款洗衣液的数量与去年用1 200元购进这款洗衣液的数量相同，当每瓶洗衣液的现售价为36元时，每周可卖出600瓶，为了能薄利多销，该超市决定降价销售，经市场调查发现，这种洗衣液的售价每降价1元，每周的销量可增加100瓶，规定这种消毒洗衣液每瓶的售价不低于进价．(1)求今年这款消毒洗衣液每瓶进价是多少元；解：设这款消毒洗衣液每瓶的售价为x元，每周的销售利润为w元，根据题意得w＝(x－24)[600＋100(36－x)]＝－100x2＋6 600x－100 800＝－100(x－33)2＋8 100， (2)当这款消毒洗衣液每瓶的售价定为多少元时，这款洗衣液每周的销售利润最大？最大利润是多少元？；∵－100＜0，∴当x＝33时，w取最大值8 100.∴当这款消毒洗衣液每瓶的售价定为33元时，这款洗衣液每周的销售利润最大，最大利润是8 100元．4【2023·十堰】 【新考向·传统文化】“端午节”吃粽子是中国传统习俗，在“端午节“来临前，某超市购进一种品牌粽子，每盒进价是40元，并规定每盒售价不得少于50元，日销售量不低于350盒．根据以往销售经验发现，当每盒售价定为50元时，日销售量为500盒，每盒售价每提高1元，日销售量减少10盒．设每盒售价为x元，日销售量为p盒．解：由题意可得，W＝(x－40)(－10x＋1 000)＝－10x2＋1 400x－40 000＝－10(x－70)2＋9 000.∵每盒售价不得少于50元，日销售量不低于350盒，(1)当x＝60时，p＝________；(2)当每盒售价定为多少元时，日销售利润W(元)最大？最大利润是多少？400　解：小强：∵50≤x≤65，设日销售额为y元，则y＝x·p＝x(－10x＋1 000)＝－10x2＋1 000x＝－10(x－50)2＋25 000，(3)小强说：“当日销售利润最大时，日销售额不是最大．”小红说：“当日销售利润不低于8 000元时，每盒售价x的范围为60≤x≤80.”你认为他们的说法正确吗？若正确，请说明理由；若不正确，请直接写出正确的结论．当x＝50时，y值最大，此时y＝25 000，当x＝65时，W值最大，此时W＝8 750，∴小强正确．小红：当日销售利润不低于8 000元时，即W≥8 000，－10(x－70)2＋9 000≥8 000，解得60≤x≤80.∵50≤x≤65，∴当日销售利润不低于8 000元时，60≤x≤65.故小红错误，当日销售利润不低于8 000元时，60≤x≤65.5【2022·仙桃】某超市销售一种进价为18元/千克的商品，经市场调查后发现，每天的销售量y(千克)与销售单价x(元/千克)有如下表所示的关系：(1)根据表中的数据在图中描点(x，y)，并用平滑曲线连接这些点，请用所学知识求出y关于x的函数表达式．解：w＝(x－18)(－x＋50)＝－x2＋68x－900＝－(x－34)2＋256，∵－1＜0，∴当x＝34时，w有最大值，∴获得最大利润时，销售单价为34元/千克． (2)设该超市每天销售这种商品的利润为w元(不计其他 成本)．①求出w关于x的函数表达式，并求出获得最大利润时，销售单价为多少；解：当w＝240时，－(x－34)2＋256＝240，解得x1＝38，x2＝30.∵超市本着“尽量让顾客享受实惠”的销售原则，∴x＝30.∴当w＝240时的销售单价为30元/千克．②超市本着“尽量让顾客享受实惠”的销售原则，求 w＝240时的销售单价．【点方法】解答本题的关键是将实际问题转化为求函数最值问题．解这类题，既要看到销售价格对销售量的影响，也要看到销售价格对单件商品利润的影响，两者结合起来，销售价格就会对销售总利润产生影响．6【2023·临沂】综合与实践：问题情境小莹妈妈的花卉超市以15元/盆的价格新购进了某种盆栽花卉，为了确定售价，小莹帮妈妈调查了附近A，B，C，D，E五家花卉店近期该种盆栽花卉的售价与日销售量情况，记录如下：数据整理(1)请将以上调查数据按照一 定顺序重新整理，填写在下表中：解：根据销售单价从小到大排列得下表：解：观察表格可知，日销售量是售价的一次函数；设日销售量为y盆，售价为x元/盆，y与x的函数关系式为y＝kx＋b，模型建立(2)分析数据的变化规律，找出日销售量与售价间的关系．解：∵每天获得400元的利润，∴(x－15)(－2x＋90)＝400，解得x＝25或x＝35，∴要想每天获得400元的利润，定价为25元/盆或35元/盆．拓广应用(3)根据以上信息，小莹妈妈在销售该种花卉中，①要想每天获得400元的利润，应如何定价？解：设每天获得的利润为w元．根据题意，得w＝(x－15)(－2x＋90)＝－2x2＋120x－1 350＝－2(x－30)2＋450.∵－2<0，∴当x＝30时，w取最大值450，∴售价定为30元/盆时，每天能够获得最大利润450元．②售价定为多少时，每天能够获得最大利润？7【2022·宁波】 【母题·教材P29问题1】为了落实劳动教育，某学校邀请农科院专家指导学生进行小番茄的种植，经过试验，其平均单株产量y(千克)与每平方米种植的株数x(2≤x≤8，且x为整数)构成一种函数关系．每平方米种植2株时，平均单株产量为4千克；以同样的栽培条件，每平方米种植的株数每增加1株，单株产量减少0.5千克．解：∵每平方米种植的株数每增加1株，单株产量减少0.5千克，∴y＝4－0.5(x－2)＝－0.5x＋5，即y关于x的函数表达式为y＝－0.5x＋5(2≤x≤8，且x为整数)．(1)求y关于x的函数表达式．解：设每平方米小番茄产量为W千克，根据题意，得W＝x(－0.5x＋5)＝－0.5x2＋5x＝－0.5(x－5)2＋12.5.∵－0.5＜0，∴当x＝5时，W取最大值，最大值为12.5.答：每平方米种植5株时，能获得最大的产量，最大产量为12.5千克．(2)每平方米种植多少株时，能获得最大的产量？最大产量为多少千克？8【2023·黄冈】 【新情景·农业应用】加强劳动教育，落实五育并举．孝礼中学在当地政府的支持下，建成了一处劳动实践基地.2023年计划将其中1 000 m2的土地全部种植甲、乙两种蔬菜．经调查发现：甲种蔬菜种植成本y(单位：元/m2)与其种植面积x(单位：m2 )的函数关系如图所示，其中200≤x≤700；乙种蔬菜的种植成本为50元/m2.500(1)当x＝________m2时，y＝35元/m2；【点拨】(2)设2023年甲、乙两种蔬菜总种植成本为W元，如何分配两种蔬菜的种植面积，使W最小？∴当x＝400时，W有最小值，最小值为42 000，此时，1 000－x＝1 000－400＝600；当600≤x≤700时，W＝40x＋50(1 000－x)＝－10x＋50 000.∵－10＜0，∴当x＝700时，W有最小值，最小值为－10×700＋50 000＝43 000，∴42 000＜43 000，∴当甲种蔬菜的种植面积为400 m2，乙种蔬菜的种植面积为600 m2时，W最小．(3)学校计划今后每年在这1 000 m2土地上，均按(2)中方案种植蔬菜，因技术改进，预计种植成本逐年下降．若甲种蔬菜种植成本平均每年下降10%，乙种蔬菜种植成本平均每年下降a%，当a为何值时，2025年的总种植成本为28 920元？解：由(2)可知，甲、乙两种蔬菜总种植成本为42 000元，且乙种蔬菜的种植成本为50×600＝30 000(元)，则甲种蔬菜的种植成本为42 000－30 000＝12 000(元)．由题意，得12 000(1－10%)2＋30 000(1－a%)2＝28 920.设a%＝m，整理，得(1－m)2＝0.64，解得m1＝0.2＝20%，m2＝1.8(不符合题意，舍去)，∴a%＝20%，∴a＝20.答：当a为20时，2025年的总种植成本为28 920元．