2024九年级数学下册第5章二次函数5.2二次函数的图像和性质4二次函数y＝ax＋h2的图像和性质习题课件新版苏科版

这是一份2024九年级数学下册第5章二次函数5.2二次函数的图像和性质4二次函数y＝ax＋h2的图像和性质习题课件新版苏科版，共29页。

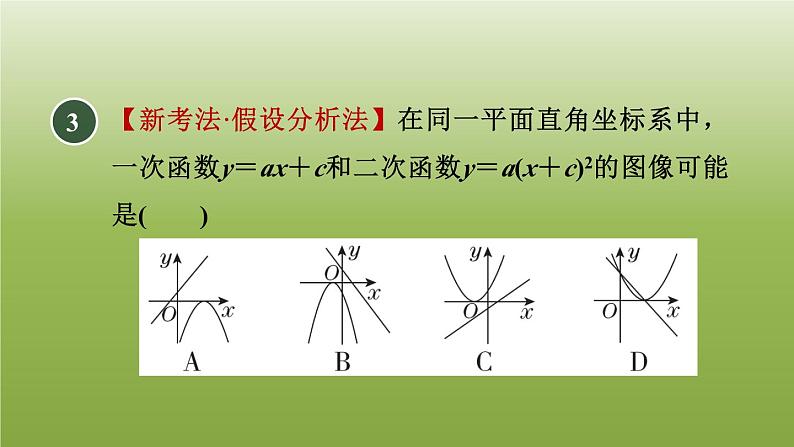
二次函数的图像和性质二次函数y＝a(x＋h)2的图像和性质5.2.4 1对于抛物线y＝2(x－1)2，下列说法正确的有(　　)①开口向上；②顶点坐标为(0，－1)；③对称轴为直线x＝1；④与x轴的交点坐标为(1，0)．A．1个 B．2个 C．3个 D．4个【点拨】抛物线y＝2(x－1)2开口向上，顶点坐标为(1，0)，对称轴为直线x＝1，与x轴的交点坐标即为它的顶点坐标 (1， 0)．故①③④正确．【答案】C2【2023·南充】若点P(m，n)在抛物线y＝ax2(a≠0)上，则下列各点在抛物线y＝a(x＋1)2上的是(　　)A．(m，n＋1) B．(m＋1，n)C．(m，n－1) D．(m－1，n)【点拨】∵抛物线y＝a(x＋1)2可看作是由抛物线y＝ax2向左平移一个单位长度得到的，∴抛物线y＝ax2上的点P(m，n)向左平移1个单位长度后，会在抛物线y＝a(x＋1)2上．故点(m－1，n)在抛物线y＝a(x＋1)2上．【答案】D3【新考法·假设分析法】在同一平面直角坐标系中，一次函数y＝ax＋c和二次函数y＝a(x＋c)2的图像可能是(　　)【点拨】A选项，由抛物线可得a＜0，由直线可得a＞0，矛盾，故错误；C选项，由抛物线可得，c＞0，由直线可得c＜0，矛盾，故错误；D选项，由抛物线可得a＞0，由直线可得 a＜0，矛盾，故错误．【答案】B4增大在函数y＝(x－1)2中，当x>1时，y随x的增大而________．(填“增大” 或“减小”)【点拨】∵y＝(x－1)2的图像开口向上，对称轴为直线x＝1，∴当x>1时，y随x的增大而增大．5已知二次函数y＝－2(x＋m)2，当x＜－3时，y随x的增大而增大；当x＞－3时，y随x的增大而减小，则当x＝1时，y的值为(　　)A．－12 B．12C．32 D．－32【点拨】二次函数y＝－2(x＋m)2的图像的对称轴为直线x＝－m，根据题意可知－m＝－3，所以m＝3，即二次函数的表达式为y＝－2(x＋3)2，所以当x＝1时，y＝－32.【答案】D6【点拨】7【母题：教材P15练习T2】把抛物线y＝x2平移得到抛物线y＝(x＋2)2，则这个平移过程正确的是(　　)A．向左平移2个单位长度B．向右平移2个单位长度C．向上平移2个单位长度D．向下平移2个单位长度A8将抛物线y＝－3x2向右平移2个单位长度，所得到的抛物线的表达式为(　　)A．y＝－3(x＋2)2 B．y＝－3(x－2)2C．y＝－3x2＋2 D．y＝－3x2－2【点拨】根据函数图像的平移规律“左加右减自变量”可知所得抛物线的表达式为y＝－3(x－2)2.【答案】B解：由题意知，这条抛物线的表达式为y＝3(x＋2)2.9已知一条抛物线的开口方向和大小与抛物线y＝3x2相同，顶点与抛物线y＝(x＋2)2相同．(1)求这条抛物线的表达式；解：将抛物线向右平移4个单位长度得到的抛物线的表达式为y＝3(x－2)2.(2)求出将上面的抛物线向右平移4个单位长度得到的抛物线的表达式．y＝－3(x－2)210【2023·宿迁中学月考】已知抛物线y＝－3x2，若抛物线不动，把y轴向左平移2个单位长度，那么在新坐标系下抛物线的表达式为________________．【点拨】由题意，可把y轴向左平移2个单位长度看作坐标轴不动，抛物线向右平移2个单位长度，然后利用平移规律求解即可．11解：由题意知，顶点A的坐标是(－1，0)，∴OA＝1.∵OA＝OB，∴OB＝1，即B(0，－1)．把B(0，－1)的坐标代入y＝a(x＋1)2，得－1＝a·12，解得a＝－1，∴y＝－(x＋1)2.如图，抛物线y＝a(x＋1)2的顶点为A，与y轴的负半轴交于点B，且OB＝OA.(1)求抛物线的表达式；解：把点C(－3，b)的坐标代入y＝－(x＋1)2，得b＝－(－3＋1)2＝－4.(2)若点C(－3，b)在该抛物线上，求b的值；解：∵抛物线y＝－(x＋1)2的对称轴是直线x＝－1，－1＜2＜3，∴y1＞y2. (3)若点D(2，y1)，E(3，y2)在此抛物线上，比较y1与y2的大小．解：∵B(1，0)，点A在抛物线y＝x2上，∴A(1，1)．∴AD＝AB＝1.∴D(2，1)．12【2023·泰州二中月考】如图，正方形ABCD的顶点A在抛物线y＝x2上，顶点B，C在x轴的正半轴上，且点B的坐标为(1，0)．(1)求点D的坐标．解：∵原抛物线y＝x2经过点O(0，0)，∴原抛物线向右平移1个单位长度得到的抛物线y＝(x－1)2经过点B(1，0)．在y＝(x－1)2中，令x＝2，则y＝(2－1)2＝1，∴点D在新抛物线上．(2)将抛物线y＝x2沿x轴适当平移，使得平移后的抛物线经过点B，求平移后抛物线的表达式，并说明你是如何平移的．此时点D在新抛物线上吗？13如图，已知二次函数y＝(x＋2)2的图像与x轴交于点A，与y轴交于点B.(1)求点A，B的坐标．解：在y＝(x＋2)2中，令y＝0，得x＝－2；令x＝0，得y＝4，∴点A，B的坐标分别为(－2，0)，(0，4)．(2)求S△AOB.抛物线的对称轴为直线x＝－2.(3)写出抛物线的对称轴．(4)在对称轴上是否存在一点P，使以P，A，O，B为顶点的四边形为平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．解：存在．①以OA和OB为邻边可作平行四边形PAOB，易求得P(－2，4)；②以AB和OB为邻边可作平行四边形PABO，易求得P(－2，－4)．综上，点P的坐标为(－2，4)或(－2，－4)．