资料中包含下列文件,点击文件名可预览资料内容






还剩7页未读,
继续阅读
成套系列资料,整套一键下载
人教版数学六下 3.3《圆柱表面积的实际应用》课件+教案(含练习+反思)
展开
这是一份人教版数学六下 3.3《圆柱表面积的实际应用》课件+教案(含练习+反思),文件包含第3课时圆柱表面积的实际应用pptx、第3课时圆柱表面积的实际应用教案docx等2份课件配套教学资源,其中PPT共13页, 欢迎下载使用。
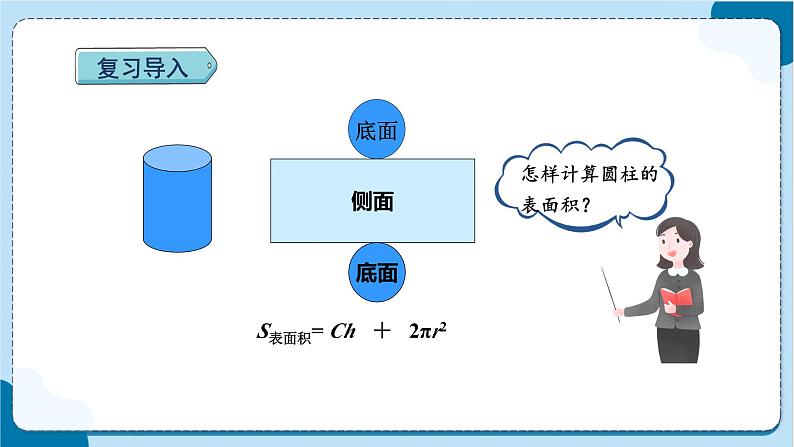
3 圆柱与圆锥复习导入侧面底面底面S表面积= Ch + 2πr2探索新知 一顶厨师帽近似圆柱形,高30 cm,帽顶直径20 cm。做这样一顶帽子大约要用多少平方厘米的面料?(得数保留整十数。)想一想:求多少面料就是求什么?“没有底”的帽子如果展开,它由哪几部分组成?这个厨师帽是圆柱形的,求用了多少面料就是求这个圆柱的表面积。“没有底”的帽子的展开图,它是由一个底面和一个侧面组成的。探索新知(1)帽子的侧面积:3.14×20×30=1884(cm2 )(2)帽顶的面积:3.14×(20÷2) 2 =314(cm2 )(3)需要用的面料:1884+314=2198≈2200(cm2 )答:做这样一顶帽子大约要用2200 cm2的面料。 一顶厨师帽近似圆柱形,高30 cm,帽顶直径20 cm。做这样一顶帽子大约要用多少平方厘米的面料?(得数保留整十数。)探索新知需要用的面料:1884+314=2198≈2200(cm2 )为什么最后的结果取2200,而不取2190呢?实际使用的面料要比计算的结果多一些,所以这类问题往往用“进一法”取近似数。想:探索新知说一说:你学会了什么?1. 如图是一个生日蛋糕,底盘是塑料板。(单位: cm)(1)请为生日蛋糕选择一个合适的蛋糕盒(单位:cm)。(在里画“√”)小试牛刀探索新知(2)这种蛋糕盒的上面和侧面都是硬纸板。制作这样一个合适的蛋糕盒至少需要多大面积的硬纸板?3. 14×28×13+3. 14×(28÷2)2=1758. 4(cm2)答:制作这样一个合适的蛋糕盒至少需要1758. 4 cm2的硬纸板。探索新知当堂练习1. 如图,从一根高2 m的圆柱形木料上截下6 dm后,木料的表面积减少了75. 36 dm2。原来这根木料的表面积是多少平方分米? 75. 36÷6÷3. 14÷2=2(dm) 2 m=20 dm3. 14×22×2+3. 14×2×2×20=276. 32(dm2)答:原来这根木料的表面积是276. 32 dm2。当堂练习2. (易错题)爸爸用铁皮做了一个圆柱形的储物桶,它的上底面留有一个直径是40 cm的圆口,做这个储物桶至少需要铁皮多少平方厘米? 3. 14×(60÷2)2×2+3. 14×60×80=20724(cm2)20724-3. 14×(40÷2)2=19468(cm2)答:做这个储物桶至少需要铁皮19468 cm2。课堂总结圆柱表面积的实际应用: 在运用圆柱表面积的计算公式解决实际问题时,要根据实际情况确定计算哪几个面的面积。特别地,如圆柱形水管没有底面、水桶只有一个底面、油桶有两个底面等。 实际使用的面料要比计算的结果多一些,所以这类问题往往用“进一法”取近似数。作 业 请完成教材练习四第2~4、6~12题。课后作业2 百分数(二)
3 圆柱与圆锥复习导入侧面底面底面S表面积= Ch + 2πr2探索新知 一顶厨师帽近似圆柱形,高30 cm,帽顶直径20 cm。做这样一顶帽子大约要用多少平方厘米的面料?(得数保留整十数。)想一想:求多少面料就是求什么?“没有底”的帽子如果展开,它由哪几部分组成?这个厨师帽是圆柱形的,求用了多少面料就是求这个圆柱的表面积。“没有底”的帽子的展开图,它是由一个底面和一个侧面组成的。探索新知(1)帽子的侧面积:3.14×20×30=1884(cm2 )(2)帽顶的面积:3.14×(20÷2) 2 =314(cm2 )(3)需要用的面料:1884+314=2198≈2200(cm2 )答:做这样一顶帽子大约要用2200 cm2的面料。 一顶厨师帽近似圆柱形,高30 cm,帽顶直径20 cm。做这样一顶帽子大约要用多少平方厘米的面料?(得数保留整十数。)探索新知需要用的面料:1884+314=2198≈2200(cm2 )为什么最后的结果取2200,而不取2190呢?实际使用的面料要比计算的结果多一些,所以这类问题往往用“进一法”取近似数。想:探索新知说一说:你学会了什么?1. 如图是一个生日蛋糕,底盘是塑料板。(单位: cm)(1)请为生日蛋糕选择一个合适的蛋糕盒(单位:cm)。(在里画“√”)小试牛刀探索新知(2)这种蛋糕盒的上面和侧面都是硬纸板。制作这样一个合适的蛋糕盒至少需要多大面积的硬纸板?3. 14×28×13+3. 14×(28÷2)2=1758. 4(cm2)答:制作这样一个合适的蛋糕盒至少需要1758. 4 cm2的硬纸板。探索新知当堂练习1. 如图,从一根高2 m的圆柱形木料上截下6 dm后,木料的表面积减少了75. 36 dm2。原来这根木料的表面积是多少平方分米? 75. 36÷6÷3. 14÷2=2(dm) 2 m=20 dm3. 14×22×2+3. 14×2×2×20=276. 32(dm2)答:原来这根木料的表面积是276. 32 dm2。当堂练习2. (易错题)爸爸用铁皮做了一个圆柱形的储物桶,它的上底面留有一个直径是40 cm的圆口,做这个储物桶至少需要铁皮多少平方厘米? 3. 14×(60÷2)2×2+3. 14×60×80=20724(cm2)20724-3. 14×(40÷2)2=19468(cm2)答:做这个储物桶至少需要铁皮19468 cm2。课堂总结圆柱表面积的实际应用: 在运用圆柱表面积的计算公式解决实际问题时,要根据实际情况确定计算哪几个面的面积。特别地,如圆柱形水管没有底面、水桶只有一个底面、油桶有两个底面等。 实际使用的面料要比计算的结果多一些,所以这类问题往往用“进一法”取近似数。作 业 请完成教材练习四第2~4、6~12题。课后作业2 百分数(二)

相关资料
更多









