北师大版数学九年级下册 1.4 《解直角三角形》课件+分层练习（含答案解析）

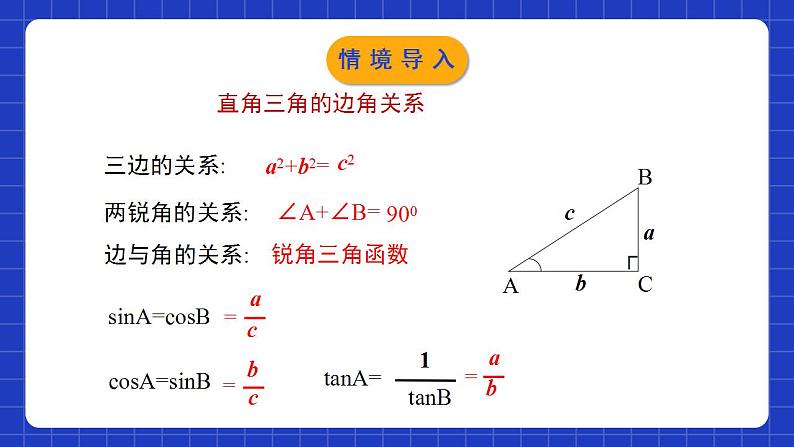
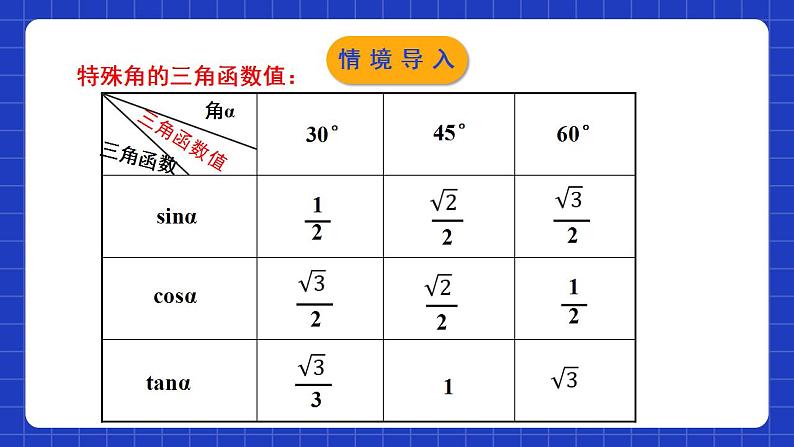
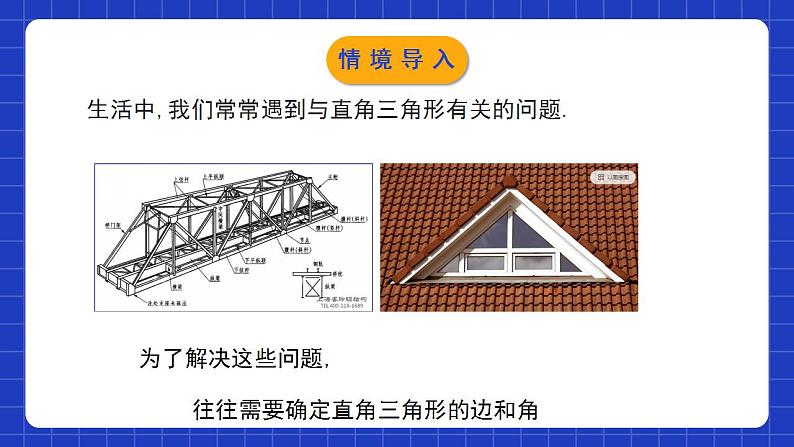
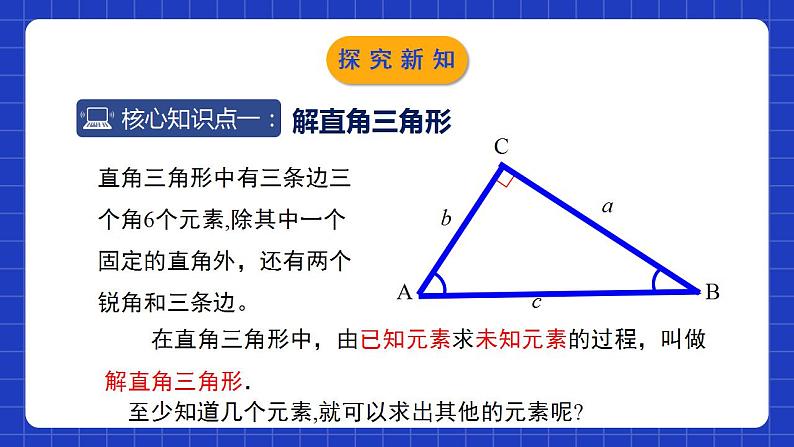
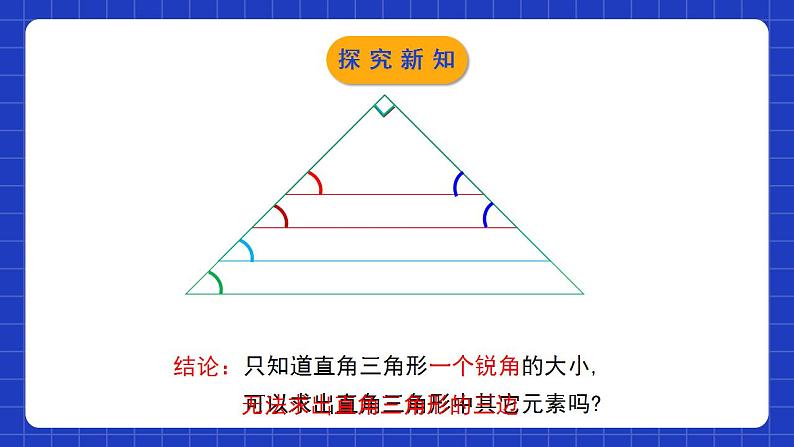
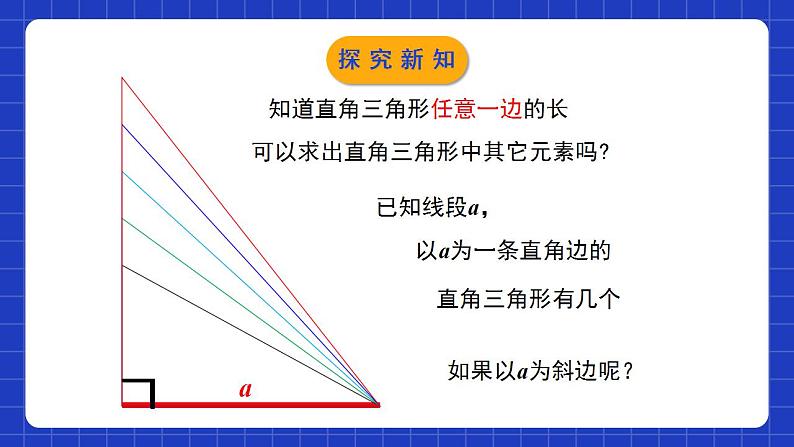
1.4解直角三角形学习目标使学生理解直角三角形中五个元素的关系，会运用勾股定理，直角三角形的两个锐角互余及锐角三角函数解直角三角形；渗透数形结合的数学思想，培养学生良好的学习习惯.两锐角的关系:三边的关系:.边与角的关系:直角三角的边角关系c2900a2+b2=∠A+∠B=锐角三角函数sinA=cosBcosA=sinBtanA=情境导入特殊角的三角函数值：  1情境导入生活中,我们常常遇到与直角三角形有关的问题.为了解决这些问题,往往需要确定直角三角形的边和角情境导入解直角三角形直角三角形中有三条边三个角6个元素,除其中一个固定的直角外，还有两个锐角和三条边。bABCac至少知道几个元素,就可以求出其他的元素呢?∟ 在直角三角形中，由已知元素求未知元素的过程，叫做解直角三角形．探究新知只知道直角三角形一个锐角的大小,可以求出直角三角形中其它元素吗?无法求出直角三角形的三边结论：探究新知∟知道直角三角形任意一边的长可以求出直角三角形中其它元素吗?已知线段a，以a为一条直角边的直角三角形有几个如果以a为斜边呢？a探究新知都无法完全求知道直角三角形任意一边的长,∟结论：出直角三角形中其它元素。a探究新知 在一个直角三角形中，已知一条边和一锐角，或者已知两条边两个元素，才能求出其他元素。 一个直角三角形中，若已知五个元素中的两个元素（其中必须有一个元素是边），则这样的直角三角形可解.探究新知 在Rt△ABC中，如果已知其中两边的长，你能求出这个三角形的其他元素吗？ 类型1 已知两边解直角三角形(1)三边之间的关系；(2)两锐角之间的关系；(3)边角之间的关系：sin A＝ ＝cos B， cos A＝ ＝sin B， tan A＝探究新知应用勾股定理求斜边，应用角的正切值求出一锐角，再利用直角三角形的两锐角互余，求出另一锐角．一般不用正弦或余弦值求锐角，因为斜边是一个中间量，如果是近似值，会影响结果的精确度．已知斜边和直角边：先利用勾股定理求出另一直角边，再求一锐角的正弦和余弦值，即可求出一锐角，再利用直角三角形的两锐角互余，求出另一锐角． 已知两直角边： 已知斜边和直角边：探究新知例1 如图，在Rt△ABC中，∠C＝90°，∠A，∠B，∠C所对的边分别为a，b，c，且 ,求这个直角三角形的其他元素.解：在Rt△ABC中，a2+b2=c2,在Rt△ABC中，探究新知例2 已知在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别为a，b，c，且c＝5，b＝4，求这个三角形的其他元素．(角度精确到1′) 由c＝5，b＝4，得sin B＝ ＝0.8，∴∠B≈53°8′.∴∠A＝90°－∠B≈36°52′.由勾股定理得解：探究新知归纳总结(1)已知a，b，怎么求∠A的度数？(2)已知a，c，怎么求∠A的度数？(3)已知b，c，怎么求∠A的度数？探究新知 已知直角三角形的一边和一锐角，解直角三角形时，若已知一直角边a和一锐角A： ① ∠B=90 °- ∠ A；②c= 若已知斜边c和一个锐角A： ① ∠ B=90°- ∠ A；②a=c·sin A ; ③b=c·cos A. 类型2 已知一边及一锐角解直角三角形探究新知例3 如图，在Rt△ABC中，∠C＝90°，∠A，∠B，∠C所对的边分别为a，b，c，∠B＝35°，b=20,求这个直角三角形的其他元素(结果保留小数点后一位).解：探究新知1、数形结合有利于分析问题；2、选择关系式时，尽量使用原始数据，以防“累积误差”和“一错再错”；3、解直角三角形时，应求出所有未知元素。注意事项：解直角三角形的原则：（1）有角先求角，无角先求边（2）有斜用弦, 无斜用切； 宁乘毋除, 取原避中。550﹖探究新知构造直角三角形解决问题例4 如图，在△ABC中，∠B=30°，∠C=45°，AC=2，求BC.D解：过点 A作 AD⊥BC于D.在△ACD中，∠C=45°，AC=2，∴CD=AD=sinC·AC=2sin45°= .在△ABD中，∠B=30°，∴BD=∴BC=CD+BD= +探究新知CABDABCE求解非直角三角形的边角问题，常通过添加适当的辅助线，将其转换为直角三角形来解.提示D归纳总结探究新知1.如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝8，则BC的长是(　　)A. B．4 C．8 D．4D2. 在△ABC中，∠C＝90°，若∠B＝2∠A，b＝3， 则a等于(　　) A. B. C．6 D.B随堂练习 B随堂练习4.如图，在Rt△ABC中，∠C=90°，∠B=30°， AB=8，则BC的长是（　　） D5.在△ABC中，AB=AC=3，BC=4，则cosB 的值是_________.随堂练习6. 如图，在Rt△ABC中，∠C＝90°，AC=6， ∠BAC的平分线 ，解这个直角三角形.6解：∵AD平分∠BAC，随堂练习 7.在Rt△ABC中， ∠C＝90° ， ∠A，∠B，∠C所对的边分别为a, b, c，根据下列条 件求出直角三角形的其他元素（角度精确到1° ): (1) 已知 a = 4, b =8; 解：在Rt△ABC中，由勾股定理得c＝ ＝ . ∵sin A＝ ＝ ＝ ， ∴∠A≈27°. ∵∠C＝90°， ∴∠B＝90°－∠A≈63°.随堂练习 解：在Rt△ABC中，∠C＝90°，∠B＝60°， ∴∠A＝30°. ∵sin B＝ ，b＝10， ∴c＝ ＝ ＝ . 由勾股定理得a＝ ＝ . (2) 已知 b =10， ∠B＝60°;随堂练习 (3) 已知 c =20， ∠A＝60°; 解：在Rt△ABC中，∠C＝90°，∠A＝60°， ∴∠B＝30°. ∵sin A＝ ，c＝20， ∴a＝c·sin A＝20×sin 60°＝20× ＝ . 由勾股定理得b＝ ＝10.随堂练习当△ABC为锐角三角形时，如图②，BC=BD+CD=12+5=17.当△ABC为钝角三角形时，如图①，∵AC=13，∴由勾股定理得CD=5∴BC=BD-CD=12-5=7；∴BC的长为7或17.当三角形的形状不确定时，一定要注意分类讨论.随堂练习解直角三角形依据解法:只要知道五个元素中的两个元素（至少有一个是边），就可以求出余下的三个未知元素勾股定理两锐角互余锐角的三角函数课堂小结课程结束