北师大版第一章 直角三角形的边角关系4 解直角三角形教课内容课件ppt

这是一份北师大版第一章 直角三角形的边角关系4 解直角三角形教课内容课件ppt，共15页。PPT课件主要包含了知识回顾，三角函数，填一填记一记，在Rt△ABC中，探究新知，你发现了什么，一角一边，解直角三角形，解直角三角形的依据，新知识等内容，欢迎下载使用。

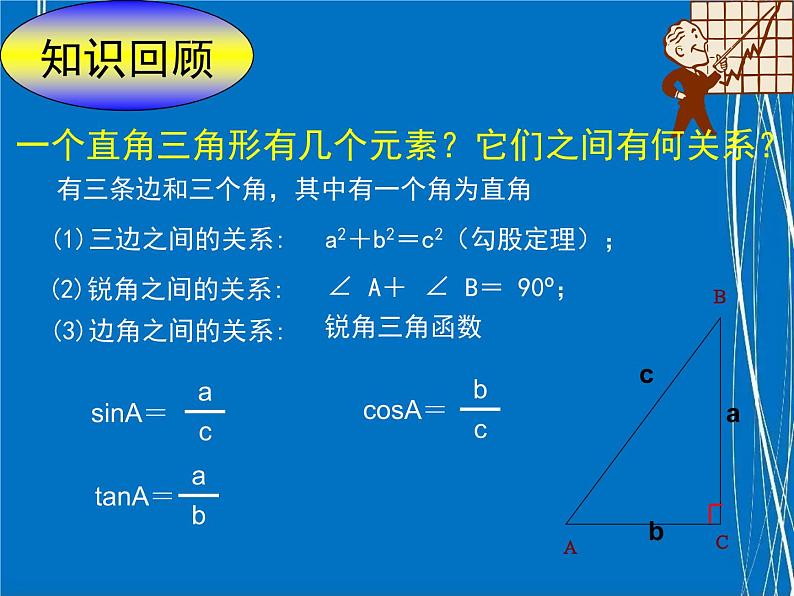
一个直角三角形有几个元素？它们之间有何关系？
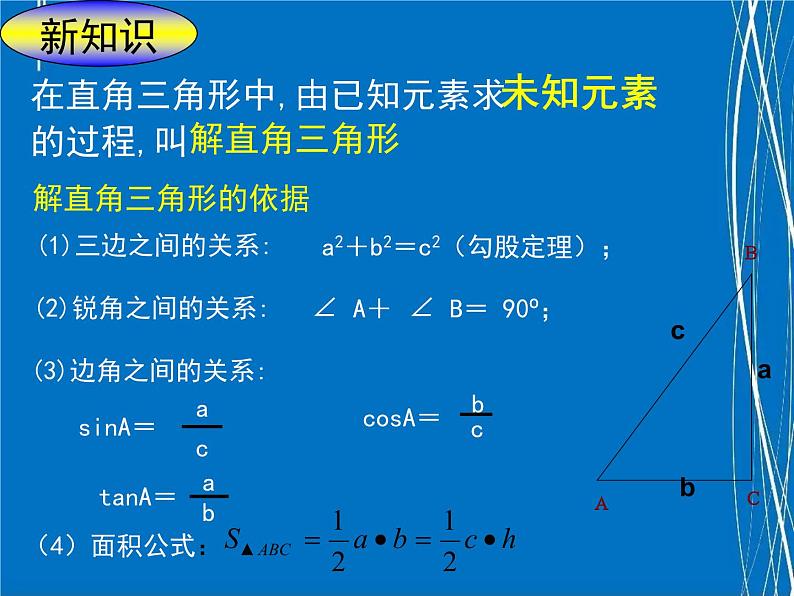
(1)三边之间的关系:
a2＋b2＝c2（勾股定理）；
(2)锐角之间的关系:
∠ A＋ ∠ B＝ 90º；
(3)边角之间的关系:
有三条边和三个角，其中有一个角为直角
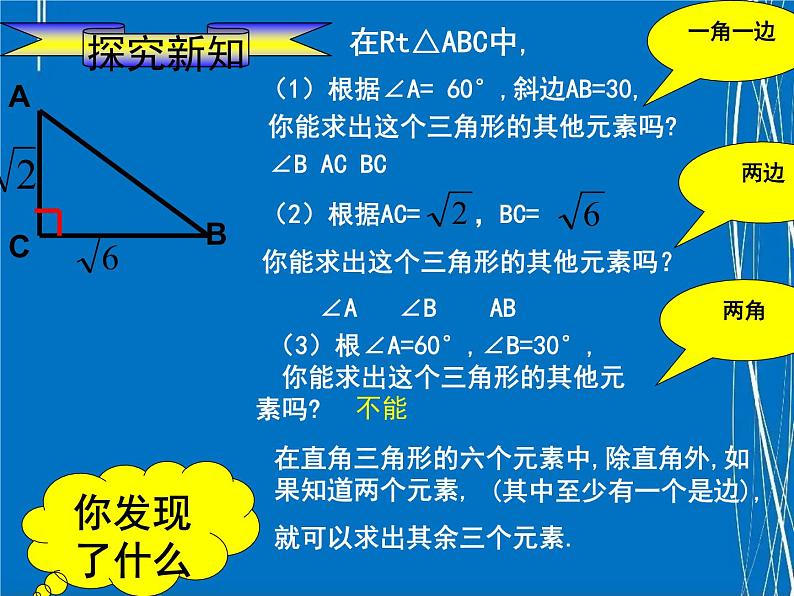
（1）根据∠A= 60°,斜边AB=30,
∠A ∠B AB
（3）根∠A=60°,∠B=30°, 你能求出这个三角形的其他元 素吗?
你能求出这个三角形的其他元素吗?
在直角三角形中,由已知元素求
在直角三角形中,由已知元素求 的过程,叫解直角三角形
例2在Rt△ABC中,∠C=90°,∠B=25°,b=30,解这个直角三角形 (精确到0.1) .
尽量选择原始数据,避免累积误差
1、在Rt△ABC 中，∠C =90°，根据下列条件求出直角三角形的其他几个元素（角度精确到 1°） （1）已知 a =4，b =8；（2）已知 b =10，∠B =60° ；（3）已知 c =20，∠A =60° ．
要想使人安全地攀上斜靠在墙面上的梯子的顶端，梯子与地面所成的角a一般要满足50°≤∠a≤75°.如果现有一个长6m的梯子，那么（1）使用这个梯子最高可以安全攀上多高的墙？（精确到0.1m）（2）当梯子底端距离墙面2.4m时，梯子与地面所成的锐角a等于多少？（精确到1°）这时人是否能够安全使用这个梯子？
问题（1）可以归结为：在Rt △ABC中，已知∠A＝75°，斜边AB＝6，求∠A的对边BC的长．
问题（1）当梯子与地面所成的角a为75°时，梯子顶端与地面的距离是使用这个梯子所能攀到的最大高度．
因此使用这个梯子能够安全攀到墙面的最大高度约是5.8m
所以 BC≈6×0.97≈5.8
由计算器求得 sin75°≈0.97
由 得
对于问题（2），当梯子底端距离墙面2.4m时，求梯子与地面所成的角a的问题，可以归结为：在Rt△ABC中，已知AC＝2.4，斜边AB＝6，求锐角a的度数
因此当梯子底墙距离墙面2.4m时，梯子与地面所成的角大约是66°
由50°＜66°＜75°可知，这时使用这个梯子是安全的．
通过本节课的学习，大家有什么收获呢？
1、课本习题1.5 1、2题2、预习下一节内容，仰角、俯角
补充作业：3 、如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.