






所属成套资源:新教材2023版高中数学新人教A版选择性必修第二册课件(22份)
- 新教材2023版高中数学第五章一元函数的导数及其应用5.2导数的运算5.2.2导数的四则运算法则课件新人教A版选择性必修第二册 课件 0 次下载
- 新教材2023版高中数学第五章一元函数的导数及其应用5.2导数的运算5.2.3简单复合函数的导数课件新人教A版选择性必修第二册 课件 0 次下载
- 新教材2023版高中数学第五章一元函数的导数及其应用5.3导数在研究函数中的应用5.3.2函数的极值与最大小值第一课时函数的极值课件新人教A版选择性必修第二册 课件 0 次下载
- 新教材2023版高中数学第五章一元函数的导数及其应用5.3导数在研究函数中的应用5.3.2函数的极值与最大小值第二课时函数的最大小值课件新人教A版选择性必修第二册 课件 0 次下载
- 新教材2023版高中数学第五章一元函数的导数及其应用5.3导数在研究函数中的应用5.3.2函数的极值与最大小值第三课时函数极值与最值的综合应用课件新人教A版选择性必修第二册 课件 0 次下载
高中数学5.3 导数在研究函数中的应用图文课件ppt
展开这是一份高中数学5.3 导数在研究函数中的应用图文课件ppt,共29页。PPT课件主要包含了新知初探·课前预习,题型探究·课堂解透,答案B,答案A等内容,欢迎下载使用。
【课标解读】1.通过数形结合感受导数与函数单调性的关系.2.掌握利用导数判断函数单调性的方法.3.能利用导数求不超过三次的多项式函数的单调区间.
【教 材 要 点】要点一 函数f(x)的单调性与导函数f′(x)的正负之间的关系在某个区间(a,b)上,如果f′(x)>0❶,那么函数y=f(x)在区间(a,b)上单调________;在某个区间(a,b)上,如果f′(x)<0❷,那么函数y=f(x)在区间(a,b)上单调________.批注❶ f′(x)>0,即函数f(x)图象的切线斜率为正,则切线的倾斜角为锐角,曲线呈上升趋势. 批注❷ f′(x)<0,即函数f(x)图象的切线斜率为负,则切线的倾斜角为钝角,曲线呈下降趋势.
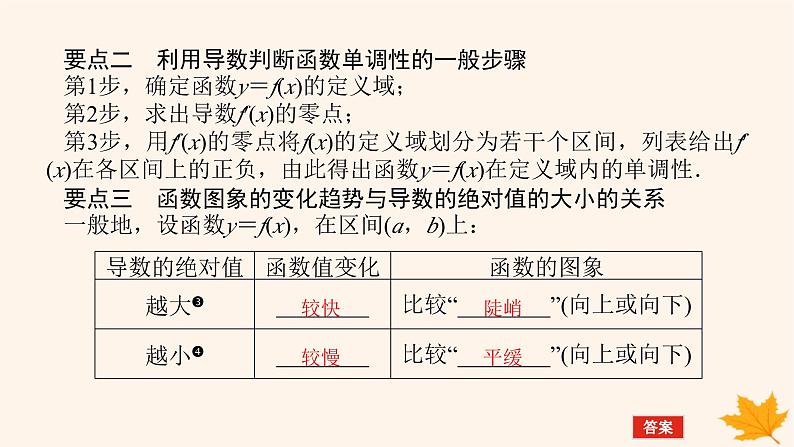
要点二 利用导数判断函数单调性的一般步骤第1步,确定函数y=f(x)的定义域;第2步,求出导数f′(x)的零点;第3步,用f′(x)的零点将f(x)的定义域划分为若干个区间,列表给出f′(x)在各区间上的正负,由此得出函数y=f(x)在定义域内的单调性.要点三 函数图象的变化趋势与导数的绝对值的大小的关系一般地,设函数y=f(x),在区间(a,b)上:
批注❸ 函数值增加得越来越快f′(x)>0越来越大;函数值减少得越来越快f′(x)<0越来越小. 批注❹ 函数值增加得越来越慢f′(x)>0越来越小;函数值减少得越来越慢f′(x)<0越来越大.
【夯 实 双 基】1.判断正误(正确的画“√”,错误的画“×”)(1)函数f(x)在定义域上都有f′(x)<0,则函数f(x)在定义域上单调递减.( )(2)函数f(x)在某区间内单调递增,则一定有f′(x)>0.( )(3)函数在某个区间上变化越快,函数在这个区间上的导数的绝对值越大.( )(4)判断函数单调性时,在区间内的个别点f′(x)=0,不影响函数在此区间的单调性.( )
2.函数y=f(x)的图象如图所示,则( )A.f′(3)>0B.f′(3)<0C.f′(3)=0D.f′(3)的符号不确定
解析:由图象可知,函数f(x)在(1,5)上单调递减,则在(1,5)上有f′(x)<0,所以f′(3)<0. 故选B.
3.函数f(x)=2x-sin x在(-∞,+∞)上是( )A.增函数 B.减函数C.先增后减 D.不确定
解析:∵f(x)=2x-sin x,∴f′(x)=2-cs x>0在(-∞,+∞)上恒成立,∴f(x)在(-∞,+∞)上是增函数.故选A.
(-∞,0),(0,+∞)
题型1 导数与函数图象的关系例1 [2022·广东广州高二期末]已知函数y=f(x)的图象是下列四个图象之一,函数y=f′(x)的图象如图所示,则函数y=f(x)图象是( )
解析:设导函数与横轴的交点为x1,x2,设-1
【方法总结】判断函数与其导函数图象关系的方法要抓住各自的关键要素,对于原函数,要重点观察其图象在哪个区间内上升或下降,而对于导函数,则应观察其函数值在哪个区间内大于零、小于零,并且这些区间与原函数的单调区间是否一致.
巩固训练1 设函数f(x)在定义域内可导,其图象如图所示,则导函数f′(x)的图象可能是( )
解析:由函数f(x)的图象,知当x<0时,f(x)是单调递减的,所以f′(x)<0;当x>0时,f(x)先减少,后增加,最后减少,所以f′(x)先负后正,最后为负.故选B.
题型2 利用导数求函数的单调区间例2 (1)已知函数f(x)=x ln x-x,求f(x)的单调区间;(2)已知函数f(x)=(x+1)eax,a∈R,求函数f(x)的单调区间.
【方法总结】利用导数求函数单调区间的三点提醒
(2)求函数f(x)=a ln x-4x-2(a∈R)的单调区间.
解析:f′(x)=x2-ax+a-1=(x-1)[x-(a-1)],令f′(x)=0得x=1或x=a-1.因为函数在区间(1,4)内为减函数,所以当x∈(1,4)时,f′(x)≤0.又函数在区间(6,+∞)上为增函数,所以当x∈(6,+∞)时,f′(x)≥0,所以4≤a-1≤6,所以5≤a≤7.即实数a的取值范围为[5,7].
【方法总结】利用导数求参数取值范围的两个策略
巩固训练3 (1)[2022·福建厦门外国语学校高二期末]若函数f(x)=(x2-ax-a)ex在区间(-2,0)内单调递减,则实数a的取值范围是( )A.[1,+∞) B.[0,+∞)C.(-∞,0] D.(-∞,1]
解析:∵f(x)=(x2-ax-a)ex,∴f′(x)=ex·[x2+(2-a)x-2a]=ex(x-a)(x+2),∵x∈(-2,0)时,ex(x+2)>0,∴若f(x)在(-2,0)内单调递减,则x-a≤0在(-2,0)上恒成立,即得a≥x在(-2,0)恒成立,∴a≥0.故选B.
相关课件
这是一份数学5.3 导数在研究函数中的应用教学ppt课件,共34页。
这是一份人教A版 (2019)选择性必修 第二册第五章 一元函数的导数及其应用5.3 导数在研究函数中的应用作业ppt课件,共31页。PPT课件主要包含了A级必备知识基础练,B级关键能力提升练,C级学科素养创新练等内容,欢迎下载使用。
这是一份人教A版 (2019)选择性必修 第二册5.3 导数在研究函数中的应用多媒体教学ppt课件,共29页。













