人教版八年级上册第十三章 轴对称13.1 轴对称13.1.1 轴对称单元测试一课一练

这是一份人教版八年级上册第十三章 轴对称13.1 轴对称13.1.1 轴对称单元测试一课一练，文件包含人教版八年级数学上册第13章轴对称单元测试卷原卷版docx、人教版八年级数学上册第13章轴对称单元测试卷解析版docx、人教版八年级数学上册第13章轴对称单元测试卷答题卡docx等3份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。

1．（2020·河北河间初二期末）第24届冬季奥林匹克运动会，将于2022年02月04日～2022年02月20日在中华人民共和国北京市和张家口市联合举行．在会徽的图案设计中，设计者常常利用对称性进行设计，下列四个图案是历届会徽图案上的一部份图形，其中不是轴对称图形的是（ ）
A．B．C．D．
【答案】D
【解析】A、不是轴对称图形，故此选项正确；
B、是轴对称图形，故此选项错误；
C、是轴对称图形，故此选项错误；
D、是轴对称图形，故此选项错误；
故选A．
2．（2020·全国初二课时练习）在平面直角坐标系中，点与点关于轴对称，则在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】C
【解析】解：∵点与点关于轴对称，
∴
∴点在第三象限，
故答案选C．
3．（2020·陕西富平初一期末）如图，把一张上下两边平行的纸条沿折叠，若，则的度数为（ ）
A．48°B．84°C．24°D．96°
【答案】B
【解析】解：如图，∵纸条的上下两边互相平行，
∴∠2+∠3=180°，
∵∠2=132°，
∴∠3=48°，
∵∠4是∠3折叠得到的，
∴∠4=∠3=48°，
∴∠1=180°－∠3－∠4=84°．
故选：B．
4．（2020·四川邛崃初一期末）如图，在中，的垂直平分线分别交，于点、，，则的长是（ ）
A．5B．6C．7D．8
【答案】C
【解析】∵DE是BC的垂直平分线，
∴CE＝BE＝7，
故选：C．
5．（2020·河南郑州外国语中学）如图，在等边三角形ABC中，BC=2，D是AB的中点，过点D作DF⊥AC于点F，过点F作EF⊥BC于点E，则BE的长为（ ）
A．1B．C．D．
【答案】C
【解析】∵D是AB的中点，
∴，
∵等边三角形ABC中∠A=∠C=60°，
且DF⊥AC，
∴∠ADF=180°-90°-60°=30°，
在Rt△ADF中，，
∴，
同理，在Rt△FEC中，，
∴．
故选：C．
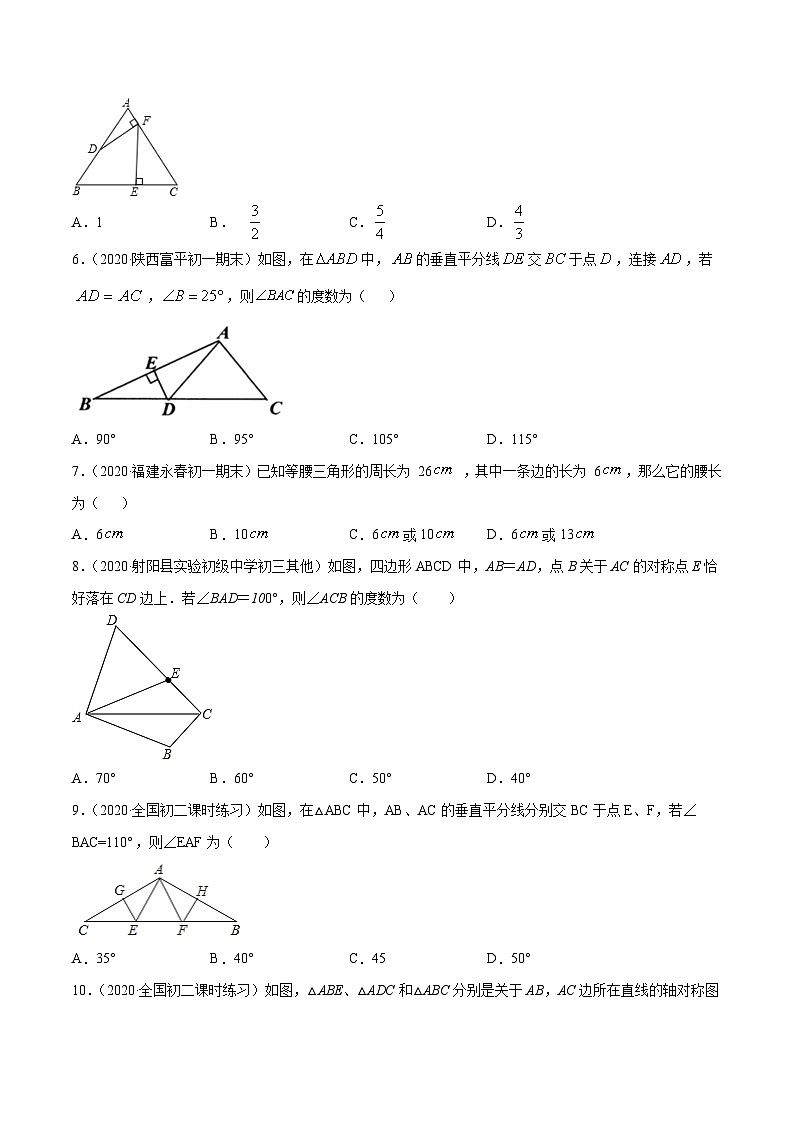
6．（2020·陕西富平初一期末）如图，在中，的垂直平分线交于点，连接，若，，则的度数为（ ）
A．90°B．95°C．105°D．115°
【答案】C
【解析】解：∵DE垂直平分AB
∴DA=DB
∴∠DAB=∠B=25°
∴∠ADC=∠DAB＋∠B=50°
∵
∴∠ADC=∠C=50°
∴∠BAC=180°－∠B－∠C=105°
故选C．
7．（2020·福建永春初一期末）已知等腰三角形的周长为 26 ，其中一条边的长为 6，那么它的腰长为（ ）
A．6B．10C．6或10D．6或13
【答案】B
【解析】①当为腰长时，则腰长为，底边=，因为，所以不能构成三角形；
②当为底边时，则腰长=，因为，所以能够成三角形；
故答案选B．
8．（2020·射阳县实验初级中学初三其他）如图，四边形ABCD中，AB＝AD，点B关于AC的对称点E恰好落在CD边上．若∠BAD＝100°，则∠ACB的度数为（ ）
A．70°B．60°C．50°D．40°
【答案】D
【解析】解：如图，连接AB'，BB'，过A作AE⊥CD于E，
∵点B关于AC的对称点B'恰好落在CD上，
∴AC垂直平分BB'，
∴AB＝AB'，
∴∠BAC＝∠B'AC，
∵AB＝AD，
∴AD＝AB'，
又∵AE⊥CD，
∴∠DAE＝∠B'AE，
∴∠CAE＝∠BAD＝50°，
∴∠ACB'＝90°﹣50°=40°，
∴∠ACB＝∠ACB'＝40°．
故选D．
9．（2020·全国初二课时练习）如图，在△ABC中，AB、AC的垂直平分线分别交BC于点E、F，若∠BAC=110°，则∠EAF为（ ）
A．35°B．40°C．45D．50°
【答案】B
【解析】解：∵∠BAC=110°，
∴∠C+∠B=70°，
∵EG、FH分别为AC、AB的垂直平分线，
∴EC=EA，FB=FA，
∴∠EAC=∠C，∠FAB=∠B，
∴∠EAC+∠FAB=70°，
∴∠EAF=40°，
故选B．
10．（2020·全国初二课时练习）如图，△ABE、△ADC和△ABC分别是关于AB，AC边所在直线的轴对称图形，若∠1：∠2：∠3=7：2：1，则∠α的度数为（ ）．
A．126°B．110°C．108°D．90°
【答案】C
【解析】∵∠1:∠2:∠3=7:2:1,
∴设∠1=7x，∠2=2x，∠3=x，
由∠1+∠2+∠3=180°得：
7x+2x+x=180°，
解得x=18，
故∠1=7×18=126°,∠2=2×18=36°,∠3=1×18=18°，
∵△ABE和△ADC是△ABC分别是关于AB，AC边所在直线的轴对称图形，
∴∠DCA=∠E=∠3=18°,∠2=∠EBA=∠D=36°,∠4=∠EBA+∠E=36°+18°=54°，
∠5=∠2+∠3=18°+36°=54°，
故∠EAC=∠4+∠5=54°+54°=108°
在△EGF与△CAF中，∠E=∠DCA，∠DFE=∠CFA，
∴∠α=∠EAC=108°.
故选C.
11．（2020·广东广州绿翠现代实验学校初二期中）如图，已知，点，，，…在射线上，点，，，…在射线上，，，，…均为等边三角形，若，则的边长为（ ）
A．8B．16C．24D．32
【答案】D
【解析】解：∵△A1B1A2为等边三角形，
∴∠B1A1A2=60°，A1B1=A1A2，
∵∠MON=30°，
∴∠OB1A1=60°-30°=30°，
∴∠MON=∠OB1A1，
∴B1A1=OA1=2，
∴△A1B1A2的边长为2，
同理得：∠OB2A2=30°，
∴OA2=A2B2=OA1+A1A2=2+2=4，
∴△A2B2A3的边长为4，
同理可得：△A3B3A4的边长为：23=8，
△A4B4A5的边长为：24=16，
则△A5B5A6的边长为：25=32，
故选：D．
12．（2020·河北怀安初二期末）如图，在△ABC中，∠BAC=45°，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，且EH=EB．下列四个结论：①∠ABC=45°；②AH=BC；③BE+CH=AE；④△AEC是等腰直角三角形.你认为正确的序号是（ ）
A．①②③B．①③④C．②③④D．①②③④
【答案】C
【解析】①∵CE⊥AB，EH＝EB，
∴∠EBH＝45°，
∴∠ABC＞45°，
故①错误；
∵CE⊥AB，∠BAC＝45°，
∴AE＝EC，
在△AEH和△CEB中，
，
∴△AEH≌△CEB（SAS），
∴AH＝BC，故选项②正确；
又EC＝EH＋CH，
∴AE＝BE＋CH，故选项③正确．
∵AE＝CE，CE⊥AB，所以△AEC是等腰直角三角形，故选项④正确．
∴②③④正确．
故选B．
13．（2020·浙江杭州初三其他）如图，△ABC是等边三角形，AD是BC边上的高，E是AC的中点，P是AD上的一个动点，当PC与PE的和最小时，∠CPE的度数是（ ）
A．30°B．45°C．60°D．90°
【答案】C
【解析】解：如连接BE，与AD交于点P，此时PE+PC最小，
∵△ABC是等边三角形，AD⊥BC，
∴PC=PB，
∴PE+PC=PB+PE=BE，
即BE就是PE+PC的最小值，
∵△ABC是等边三角形，
∴∠BCE=60°，
∵BA=BC，AE=EC，
∴BE⊥AC，
∴∠BEC=90°，
∴∠EBC=30°，
∵PB=PC，
∴∠PCB=∠PBC=30°，
∴∠CPE=∠PBC+∠PCB=60°，
故选：C．
14．（2020·黑龙江虎林初二期末）如图，过边长为 1 的等边△ABC 的边 AB 上一点 P，作 PE⊥AC 于 E，Q 为 BC 延长线上一点，当 PA=CQ 时，连PQ 交 AC 边于 D，则 DE 的长为（ ）
A．0.5B．1C．0.25D．2
【答案】A
【解析】过P作PM∥BC，交AC于M；
∵△ABC是等边三角形，且PM∥BC，
∴△APM是等边三角形，
又∵PE⊥AM，
∴；（等边三角形三线合一）
∵PM∥CQ，
∴∠PMD=∠QCD，∠MPD=∠Q；
又∵PA=PM=CQ，
在△PMD和△QCD中
，
∴△PMD≌△QCD（AAS），
∴，
∴，
故选A．
二、填空题（本题共4个小题；每个小题3分，共12分，把正确答案填在横线上）
15．（2020·山东招远初一期末）如图，AD是等边三角形ABC的中线，AE=AD，则∠EDC=______．
【答案】15°
【解析】∵AD是等边△ABC的中线，
∴AD⊥BC，∠BAD=∠CAD=∠BAC=×60°=30°，
∴∠ADC=90°，
∵AD=AE，
∴∠ADE=∠AED==75°，
∴∠EDC=∠ADC-∠ADE=90°-75°=15°．
故答案为15°．
16．（2020·吉林长春初一期末）如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上。若PM=2.5cm,PN=3cm,MN=4cm,则线段QR的长为__________cm。
【答案】4.5
【解析】∵点P、Q关于OA对称，点P、R关于OB对称，
∴OA垂直平分PQ，OB垂直平分PR，
∴QM=PM=2.5cm，NR=PN=3cm，
∴QR=NR+MN-QM=3+4-2.5=4.5（cm）.
17．（2020·四川邛崃初一期末）等腰三角形一腰上的高与另一腰的夹角为50°，则这个等腰三角形的一个底角的度数为_____．
【答案】或
【解析】如图1：
∵
∴
如图2：
∵
∴
∴
故答案为：70°或20°．
18．（2020·湖南茶陵初二期末）如图，已知钝角，依下列步骤尺规作图，并保留作图痕迹．步骤1：以为圆心，为半径画弧①；步骤2：以为圆心，为半径画弧②；步骤3：连接，交延长线于点；下列结论：①垂直平分线段；②平分；③；④．其中一定正确的有_________（只填序号）
【答案】①③④
【解析】连接CD，BD
由作图可知：CA=CD，BA=BD，
∴直线BC垂直平分线段AD，
∴AH=DH，
∴S△ABC=•BC•AH，
故①③④正确，
故答案为：①③④．
三、解答题（本题共8道题，19-21每题6分，22-25每题8分，26题10分，满分60分）
19．（2020·四川邛崃初一期末）如图，在边长为1的小正方形组成的网格中，四边形的四个顶点均在格点上．请按要求完成下列各题：
（1）在网格中画出四边形关于直线对称的四边形；
（2）求四边形的面积．
【答案】（1）详见解析；（2）7.5
【解析】（1）如图所示

（2）
20．（2020·河北河间初二期末）如图，△ABC与△ADE关于直线MN对称，BC与DE的交点F在直线MN上．若ED=4cm，FC=lcm，∠BAC=76°，∠EAC=58°
（1）求出BF的长度；
（2）求∠CAD的度数；
【答案】（1）3cm；（2）18°
【解析】解：（1）∵△ABC与△ADE关于直线MN对称，ED=4cm，
∴BC=ED=4cm，
又∵FC=1cm，
∴BF=BC﹣FC=3cm．
（2）∵△ABC与△ADE关于直线MN对称，∠BAC=76°，∠EAC=58°，
∴∠EAD=∠BAC=76°，
∴∠CAD=∠EAD﹣∠EAC=76°﹣58°=18°．
21．（2020·广东英德初三二模）作图题：（要求保留作图痕迹，不写作法）
（1）作△ABC中BC边上的垂直平分线EF（交AC于点E，交BC于点F）；
（2）连结BE，若AC=10，AB=6，求△ABE的周长．
【答案】（1）答案见解析；（2）16．
【解析】解：(1)如图所示，
(2)∵EF垂直平分BC，
∴BE=EC，
∴△ABE的周长=AB+BE+AE=AB+BE+EC=AB+BC，
∵AB=6，BC=10，
∴△ABE的周长=6+10=16．
22．（2020·全国初三专题练习）如图，点A，D，B，E在同一条直线上，，，
（1）证明：
（2）当时，请判断是什么三角形，并说明理由．
【答案】（1）见解析；（2）等边三角形；见解析．
【解析】（1）∵
∴
∴在与中

∴
（2）等边三角形，理由如下：
由（1）得
∴
∴
∵
∴
∴是等边三角形．
23．（2020·陕西富平初二期末）如图，在中，平分，且，连接，延长AD到E，使得．
求证：（1）
（2）为等腰三角形．
【答案】（1）证明见解析；（2）证明见解析．
【解析】（1）证明：
平分
（2）
是等腰三角形；
24．（2020·陕西富平初一期末）如图，在中，，点在上，又在的垂直平分线上，点在的延长线上，点在上，．
（1）试说明：．
（2）若平分，求的度数．
【答案】（1）见解析；（2）36º
【解析】解：（1）∵点在的垂直平分线上，
∴，
∴，
在△和△中，
∵，，，
∴△≌△（SAS）；
（2）∵，
∴，
∵平分，，
∴，
∴，
∵，
∴，
由（1）知，△≌△，
∴，
∵，
∴．
25．（2020·河北高阳初二期末）数学课上，同学们探究下面命题的正确性：顶角为36°的等腰三角形具有一种特性，即经过它某一顶点的一条直线可把它分成两个小等腰三角形．为此，请你解答下列问题：
（1）已知：如图，在△ABC中，AB=AC，∠A=36°，直线BD平分∠ABC交AC于点D．求证：△ABD与△DBC都是等腰三角形；
（2）在证明了该命题后，小乔发现：当∠A≠36°时，一些等腰三角形也具有这样的特性，即经过等腰三角形某一顶点的一条直线可以把该等腰三角形分成两个小等腰三角形．则∠A的度数为______（写出两个答案即可）；并画出相应的具有这种特性的等腰三角形及分割线的示意图，并在图中标出两个小等腰三角形的各内角的度数．
（3）接着，小乔又发现：其它一些非等腰三角形也具有这样的特性，即过它其中一个顶点画一条直线可以将原三角形分成两个小等腰三角形．请你画出一个具有这种特性的三角形的示意图，并在图中标出两个小等腰三角形的各内角的度数．
【答案】（1）见解析；（2）90°或108°或；（3）见解析
【解析】（1）证明：在△ABC中，
∵AB=AC，∠A=36°
∴∠ABC=∠C=（180°－∠A）=72°
∵BD平分∠ABC，
∴∠1=∠2=36°
∴∠1=∠A
∴AD=BD
∴△ABD是等腰三角形
∵∠BDC=∠1+∠A=72°
∴∠BDC=∠C=72°
∴BD=BC，
∴△BDC是等腰三角形
（2）如下图所示：
∴顶角∠A的度数为90°或108°或，
故答案为：90°或108°或；
（3）如图所示．
26．（2020·济南市长清区实验中学初一期中）在等腰直角△ABC中，AB=AC，∠BAC=90°，以CA为边在∠ACB的另一侧作∠ACM=∠ACB，点D为射线BC上任意一点，在射线CM上截取CE=BD，连接AD、DE、AE．
（1）如图1，当点D落在线段BC的延长线上时，直接写出∠ADE的度数；
（2）如图2，当点D落在线段BC(不含边界)上时，AC与DE交于点F，请问（1）中的结论是否仍成立？如果成立，请给出证明；如果不成立，请说明理由；
（3）如图2，作AH⊥BC，垂足为H，作AG⊥EC，垂足为G，连接HG，判断△GHC的形状，并说明理由．
【答案】（1）∠ADE=45°；（2）成立，见详解；（3）△GHC为等腰直角三角形．
【解析】解：（1）∠ADE=45°
∵在等腰直角△ABC中，∠BAC=90°，AB=AC，
∴∠B=∠ACB=45°，
∵∠ACM=∠ACB，
∴∠B=∠ACM=45°，
在△ABD和△ACE中，
，
∴△ABD≌△ACE，
∴AD=AE，∠BAD=∠CAE，
∵∠BAD=∠BAC+∠CAD，∠CAE=∠DAE+∠CAD，∠BAC=90°，
∴∠DAE=∠BAC=90°，
∴△DAE是等腰直角三角形，
∴∠ADE=45°；
（2）成立
∵在等腰直角△ABC中，∠BAC=90°，AB=AC，
∴∠B=∠ACB=45°，
∵∠ACM=∠ACB，
∴∠B=∠ACM=45°，
在△ABD和△ACE中，
，
∴△ABD≌△ACE，
∴AD=AE，∠BAD=∠CAE，
∵∠BAC=∠BAD+∠CAD，∠DAE=∠CAE+∠CAD，∠BAC=90°，
∴∠DAE=∠BAC=90°，
∴△DAE是等腰直角三角形，
∴∠ADE=45°；
（3）△GHC为等腰直角三角形
如图，
∵AH⊥BC，AG⊥EC，
∴∠AHB=∠AHC=∠AGC=90°，
在△ABH和△ACG中，
，
∴△ABH≌△ACG，
∴AH=AG，
∵∠ACH=∠ACG=45°，∠AHC=∠AGC=90°，
∴△AHC和△AGC为等腰直角三角形，即AG=CG，AH=HC，
又∵∠B=∠ACB=45°，∠ACM=∠ACB，
∴∠BCM=90°，
∴△GHC为等腰直角三角形．