初中数学苏科版八年级上册6.4 用一次函数解决问题精品练习

这是一份初中数学苏科版八年级上册6.4 用一次函数解决问题精品练习，共12页。试卷主要包含了10x＋800等内容，欢迎下载使用。

一、选择题
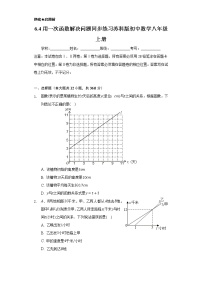
1.如图所示为一台自动测温记录仪的图象，它反映了某市冬季某天气温T与时间t之间的关系，观察图象得到下列信息，其中错误的是( )
A.凌晨4时气温最低，为－3 ℃
B.14时气温最高，为8 ℃
C.从0时至14时，气温随时间增加而上升
D.从14时至24时，气温随时间增加而下降
2.如图，一个函数的图象由射线BA、线段BC、射线CD组成，其中点A(﹣1，2)，B(1，3)，C(2，1)，D(6，5)，则此函数( )
A.当x＜1时，y随x的增大而增大
B.当x＜1时，y随x的增大而减小
C.当x＞1时，y随x的增大而增大
D.当x＞1时，y随x的增大而减小
3.今年“五一”节，小明外出爬山，他从山脚爬到山顶的过程中，中途休息了一段时间，设他从山脚出发后所用时间为t(分钟)，所走的路程为s(米)，s与t之间的函数关系如图所示.下列说法错误的是( )
A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6 600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
4.小华同学接到通知，她的作文通过了《我的中国梦》征文选拔，需尽快上交该作文的电子文稿，接到通知后，小华立即在电脑上打字录入这篇文稿，录入一段时间后因事暂停，过了一小会儿，小华继续录入并加快了录入速度，直至录入完成，设从录入文稿开始所经过的时间为x，录入字数为y，下面能反映y与x之间的关系的大致图象是（ ）
A. B. C. D.
5.某学校组织团员举行“伏羲文体旅游节”宣传活动，从学校骑自行车出发，先上坡到达甲地后，宣传了8分钟，然后下坡到乙地又宣传了8分钟返回，行程情况如图所示.若返回时，上、下坡速度保持不变，在甲地仍要宣传8分钟，那么他们从乙地返回学校所用的时间是( )
A.33分钟 B.46分钟 C.48分钟 D.45.2 分钟
6.某通讯公司就上宽带网推出A，B，C三种月收费方式.这三种收费方式每月所需的费用y(元)与上网时间x(h)的函数关系如图所示，则下列判断错误的是( )
A.每月上网时间不足25 h时，选择A方式最省钱
B.每月上网费用为60元时，B方式可上网的时间比A方式多
C.每月上网时间为35 h时，选择B方式最省钱
D.每月上网时间超过70 h时，选择C方式最省钱
7.如图，在物理课上，老师将挂在弹簧测力计下端的铁块浸没在水中，然后缓慢匀速向上提起，直至铁块完全露出水面一定高度，则下图能反映弹簧测力计的读数y(单位：N)与铁块被提起的高度x(单位：cm)之间的函数关系的大致图象是( )

8.据调查，某地铁自行车存放处在某星期天的存车量为4 000辆次，其中变速车存车费是每辆一次0.30元，普通自行车存车费是每辆一次0.20元，若普通自行车存车数为x辆，存车费总收入为y元，则y关于x的函数关系式为( )
A.y＝0.10x＋800(0≤x≤4 000)
B.y＝0.10x＋1 200(0≤x≤4 000)
C.y＝－0.10x＋800(0≤x≤4 000)
D.y＝－0.10x＋1 200(0≤x≤4 000)
9.体育课上，20人一组进行足球比赛，每人射点球5次，已知某一组的进球总数为49个，进球情况记录如下表，其中进2个球的有x人，进3个球的有y人，若(x,y)恰好是两条直线的交点坐标，则这两条直线的解析式是( )
A.y＝x＋9与y＝eq \f(2,3)x＋eq \f(22,3) B.y＝﹣x＋9与y＝eq \f(2,3)x＋eq \f(22,3)
C.y＝﹣x＋9与y＝﹣eq \f(2,3)x＋eq \f(22,3) D.y＝x＋9与y＝﹣eq \f(2,3)x＋eq \f(22,3)
10.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米，先到终点的人原地休息.已知甲先出发2秒.在跑步过程中，甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示，给出以下结论：①a=8；②b=92；③c=123.其中正确的是( )

A.①②③ B.仅有①② C.仅有①③ D.仅有②③
二、填空题
11.某商店出售茶杯，茶杯的个数与钱数之间的关系，如图所示，由图可得每个茶杯_______元.
12.甲、乙两人在一次赛跑中，路程s与时间t的关系如图所示，根据图象回答：这是一次____米赛跑；先到达终点的是____；乙的速度是________.
13.甲、乙两人骑自行车匀速同向行驶，乙在甲前面100米处，同时出发去距离甲1300米的目的地，其中甲的速度比乙的速度快.设甲、乙之间的距离为y米，乙行驶的时间为x秒，y与x之间的关系如图所示.则甲的速度为每秒 米.
14.某水果批发市场苹果的价格如下表：
如果二班的数学余老师购买苹果x千克(x大于40千克)付了y元，那么y关于x的函数关系式为 .
15.如图，A.B两地相距200km，一列火车从B地出发沿BC方向以120km/h的速度行驶，在行驶过程中，这列火车离A地的路程y(km)与行驶时间t(h)之间的函数关系式是_____
16.设甲、乙两车在同一直线公路上匀速行驶，开始甲车在乙车的前面，当乙车追上甲车后，两车停下来，把乙车的货物转给甲车，然后甲车继续前行，乙车向原地返回.设x秒后两车间的距离为y米，关于y与x的函数关系如图所示，则甲车的速度是 米/秒.
三、解答题
17.某城市电业局为鼓励居民节约用电，采取按月用电量分段收费办法，居民应交电费y(元)与用电量x(度)的函数关系如图所示．
(1)分别求出当0≤x<50和x≥50时，y与x的函数关系式
(2)若某居民该月用电65度，则应交电费多少元?

18.有一天，龟、兔进行了600米赛跑，如图表示龟兔赛跑的路程s(米)与时间t(分钟)的关系(兔子睡觉前后速度保持不变)，根据图象回答以下问题：
(1)赛跑中，兔子共睡了多少时间？
(2)赛跑开始后，乌龟在第几分钟时从睡觉的兔子旁经过？
(3)兔子跑到终点时，乌龟已经到了多长时间？并求兔子赛跑的平均速度．
19.某天早晨，王老师从家出发步行前往学校，途中在路边一饭店吃早餐，如图所示是王老师从家到学校这一过程中所走的路程S（米）与时间t(分)之间的关系.
（1）学校离他家 米，从出发到学校，王老师共用了 分钟；
（2）王老师吃早餐用了多少分钟？
（3）王老师吃早餐以前的速度快还是吃完早餐以后的速度快？吃完早餐后的平均速度是多少？
20.为保护学生视力，课桌椅的高度都是按一定的关系配套设计的，研究表明：假设课桌的高度为y(cm)，椅子的高度为x(cm)，则y是x的一次函数，如表列出了两套符合条件的课桌椅的高度：
(1)请确定课桌高度y与椅子高度x之间的函数表达式．
(2)现有一张高80 cm的课桌和一张高为43 cm的椅子，它们是否配套？为什么？
21.学校田径运动会快要举行了，小刚用自己平时积攒的零花钱买了一双运动鞋，他发现鞋码与脚的大小不是1∶1的关系，爱动脑筋的他就想研究一下，到底鞋码与脚的大小是怎样一种关系，于是小刚回家量了量妈妈36码的鞋子，内长是23 cm，量了量爸爸42码的鞋子，内长是26 cm，又量了量自己买的鞋子，内长是24.5 cm.他认真思考，觉得鞋子内长x与鞋子号码y之间隐约存在一次函数关系，你能帮助小刚求出这个一次函数的表达式吗？小刚买的鞋是多大码的？
22.某地城管需要从甲、乙两个仓库向A、B两地分别运送10吨和5吨的防寒物资，甲、乙两仓库分别有8吨、7吨防寒物资．从甲、乙两仓库运送防寒物资到A、B两地的运费单价(元/吨)如表1，设从甲仓库运送到A地的防寒物资为x吨(如表2)．
(表1)
(表2)
(1)完成表2；
(2)求运送的总运费y(元)与x(吨)之间的函数表达式，并直接写出x的取值范围；
(3)直接写出最低总运费．
23.某农场急需氨肥8 t，在该农场南北方向分别有A，B两家化肥公司，A公司有氨肥3 t，每吨售价750元；B公司有氨肥7 t，每吨售价700元，汽车每千米的运输费用b(元/千米)与运输质量a(t)的关系如图所示．
(1)根据图象求出b关于a的函数表达式，并写出自变量的取值范围．
(2)若农场到B公司的路程是农场到A公司路程的2倍，农场到A公司的路程为m(km)，设农场从A公司购买x(t)氨肥，购买8 t氨肥的总费用为y元(总费用＝购买氨肥的费用＋运输费用)，求出y关于x的函数表达式(m为常数)，并向农场建议总费用最低的购买方案．
答案
1.C
2.A
3.C
4.C
5.D
6.D
7.D
8.D
9.C
10.A
11.答案为：2.
12.答案为：100 甲 8米/秒
13.答案为：6
14.答案为：y=6x(x＞40)；
15.答案为：y＝200＋120t(t≥0).
16.答案为：20；
17.
18.解：(1)40分钟；
(2)200÷(600÷60)=20(分)，即赛跑开始后，乌龟在第20分钟从睡觉的兔子旁经过；
(3)(600－200)÷(200÷10)=20(分)，50＋20－60=10(分)，即乌龟已经到了10分钟；兔子赛跑的平均速度是600÷(50＋20)=60/7(米/分)
19.解：（1）学校距他家1000米，王老师用25分钟；
（2）王老师吃早餐用了20-10=10分钟；
（3）吃完早餐以后速度快，（1000-500）÷（25-20）=100（米/分）.
20.解：(1)设一次函数的表达式为y＝kx＋b(k≠0)，
由题意，得eq \b\lc\{(\a\vs4\al\c1(74＝42k＋b,70＝38k＋b，))解得eq \b\lc\{(\a\vs4\al\c1(k＝1，,b＝32，))
∴y＝x＋32.
(2)当x＝43时，y＝43＋32＝75≠80，
∴它们不配套．
21.解：设这个一次函数表达式为y＝kx＋b(k≠0)，其中y为鞋子的码数，x为鞋子的内长．
由题意，得eq \b\lc\{(\a\vs4\al\c1(23k＋b＝36，,26k＋b＝42，))解得eq \b\lc\{(\a\vs4\al\c1(k＝2，,b＝－10.))
∴y＝2x－10.
当x＝24.5时，y＝2×24.5－10＝39，
∴小刚买的鞋是39码的．
22.解：(1)设从甲仓库运送到A地的防寒物资为x吨，可得从甲仓库运送到B地的防寒物资为8﹣x吨，从乙仓库运送到B地的防寒物资为x﹣3吨；
故答案为：8﹣x、x﹣3；
(2)运送的总运费y(元)与x(吨)之间的函数表达式为：
y＝80x+100(10﹣x)+50(8﹣x)+30(x﹣3)，
从而：y＝﹣40x+1310．其中，3≤x≤8．
(3)由(2)得y＝﹣40x+1310，y随x增大而减少，所以当x＝8时总运费最小，
当x＝8时，y＝﹣40×8+1310＝990，最低总运费为990元．
23.解：(1)当0≤a≤4时，设b＝ka(k≠0)．
把点(4，12)的坐标代入，得4k＝12，
解得k＝3.
∴b＝3a.
当a≥4时，设b＝ma＋n(m≠0)．
把点(4，12)，(8，32)的坐标分别代入，得
eq \b\lc\{(\a\vs4\al\c1(4m＋n＝12，,8m＋n＝32，))解得eq \b\lc\{(\a\vs4\al\c1(m＝5，,n＝－8.))
∴b＝5a－8.
∴b＝eq \b\lc\{(\a\vs4\al\c1(3a（0≤a≤4），,5a－8（a≥4）.))
(2)∵A公司有氨肥3 t，B公司有氨肥7 t，
∴0≤x≤3，0≤8－x≤7，∴1≤x≤3，
∴y＝750x＋3mx＋(8－x)×700＋[5(8－x)－8]×2m
＝(50－7m)x＋5600＋64m.
∴当m＞eq \f(50,7)时，到A公司买3 t，B公司买5 t费用最低；
当m＝eq \f(50,7)时，到A公司或B公司买费用一样；
当m＜eq \f(50,7)时，到A公司买1 t，B公司买7 t，费用最低．
购买苹果数
(千克)
不超过
20千克
20千克以上
但不超过40千克
40千克以上
每千克价格
8元
7元
6元
第一套
第二套
椅子高度x(cm)
42
38
课桌高度y(cm)
74
70
甲仓库
乙仓库
A地
80
100
B地
50
30
甲仓库
乙仓库
A地
x
10﹣x
B地