初中数学人教版八年级上册13.3.1 等腰三角形复习练习题

第十三章 轴对称

第6课时　13.3.1等腰三角形（2）

一、课前小测——简约的导入

1. 有下列长度的三条线段，能组成等腰三角形的是（   ）.

A．2cm，2cm，4cm   B．3cm，8cm，3cm  

C．3cm，4cm，6cm   D．5cm，4cm，4cm

2. 等腰三角形的一个外角等于100°，则与它不相邻的两个内角的度数分别为（    ）.

A．40°，40°       B．80°，20°  

C．50°，50°       D．50°，50°或80°，20°

二、典例探究——核心的知识

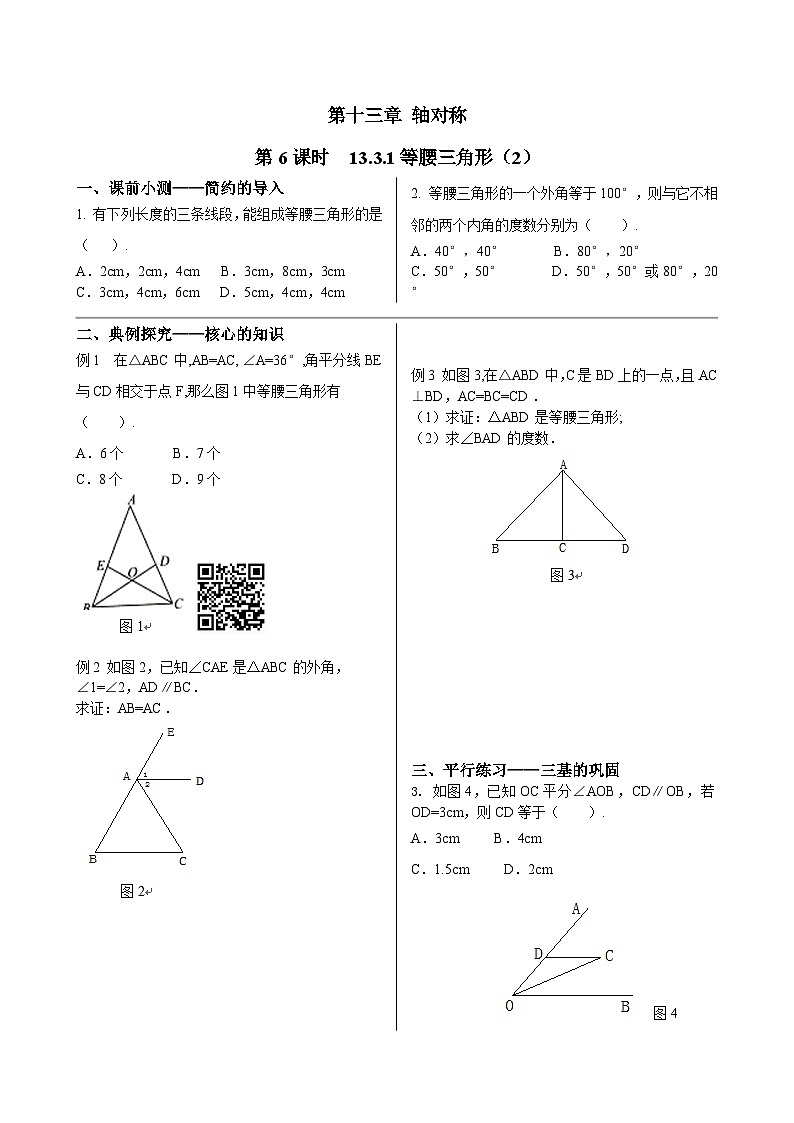
例1  在△ABC中,AB=AC,∠A=36°,角平分线BE与CD相交于点F,那么图1中等腰三角形有（    ）.

A．6个       B．7个

C．8个       D．9个

例2 如图2，已知∠CAE是△ABC的外角，

∠1=∠2，AD∥BC．

求证：AB=AC．

例3 如图3,在△ABD中，C是BD上的一点，且AC⊥BD，AC=BC=CD．

（1）求证：△ABD是等腰三角形;

（2）求∠BAD的度数．

三、平行练习——三基的巩固

3. 如图4，已知OC平分∠AOB，CD∥OB，若OD=3cm，则CD等于（    ）.

A．3cm     B．4cm    

C．1.5cm     D．2cm

           图4

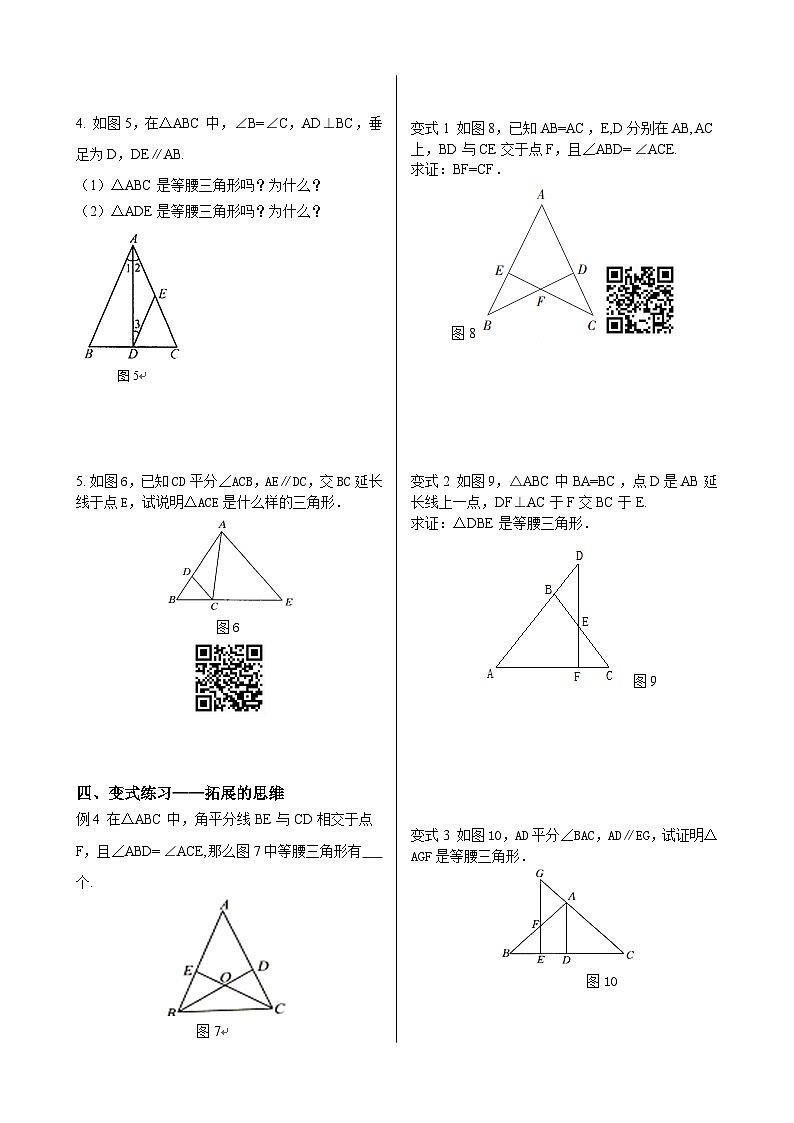
4. 如图5，在△ABC中，∠B=∠C，AD⊥BC，垂足为D，DE∥AB.

（1）△ABC是等腰三角形吗？为什么？

（2）△ADE是等腰三角形吗？为什么？

5. 如图6，已知CD平分∠ACB，AE∥DC，交BC延长线于点E，试说明△ACE是什么样的三角形．

                    图6

四、变式练习——拓展的思维

例4 在△ABC中，角平分线BE与CD相交于点F，且∠ABD=∠ACE,那么图7中等腰三角形有    个.

变式1 如图8，已知AB=AC，E,D分别在AB,AC上，BD与CE交于点F，且∠ABD=∠ACE.

求证：BF=CF．

图8

变式2 如图9，△ABC中BA=BC，点D是AB延长线上一点，DF⊥AC于F交BC于E.

求证：△DBE是等腰三角形．

图9

变式3 如图10，AD平分∠BAC，AD∥EG，试证明△AGF是等腰三角形．

                     图10

五、课时作业——必要的再现

6．如图11，在△ABC中，AB=AC，D为BA延长线上的一点，AE平分∠DAC，那么AE∥BC吗？说说你的理由．

7. 如图12，在△ABC中，D在BC上，若AD=BD，

AB=AC=CD，求∠ABC的度数．

8. 如图13，∠BAC=90°, AF是△ABC的角平分线，BD⊥AF交AF的延长线于D，DE∥AC交AB于E，求证：AE=BE．

图13

9. 如图14，在△ABC中，AB=AC，AF⊥BC，点D在BA的延长线上,点E在AC上，且AD=AE，试探索DE与AF的位置关系，并证明你的结论．

答案

1. D.

2. D.

例1 C.

例2 ∵AD∥BC，

∴∠1=∠B,∠2=∠C．

又∵∠1=∠2，

∴∠B=∠C，

∴AB=AC（等角对等边）．

例3 （1）∵AC⊥BD，

∴∠ACB=∠ACD=90°．

又∵AC=AC，BC=CD，

∴△ACB≌△ACD（SAS）．

∴AB=AD．

∴△ABD是等腰三角形;

（2）由（1）可知AB=AD，

∴∠B=∠D．

又∵AC=BC，

∴∠B=∠BAC，AC=CD．

∴∠D=∠DAC（等边对等角）．

在△ABD中，∠B+∠D+∠BAC+∠DAC=180°，

∴2（∠BAC+∠DAC）=180°．

∴∠BAC+∠DAC=90°，

即∠BAD=90°．

3. A.

4. △ABC是等腰三角形.

∵ ∠B=∠C,

∴ AB=AC,

∴△ABC是等腰三角形;

(2) △ADE是等腰三角形.

∵AB=AC, AD⊥BC,

∴∠1=∠2.

∵DE∥AB,

∴∠1=∠3,

∴∠2=∠3,

∴AE=DE,

∴△ADE是等腰三角形.

5. △ACE是等腰三角形．

∵AE∥DC，

∴∠ACD=∠CAE，∠BCD=∠E．

又∵CD平分∠ACB，

∴∠ACD=∠BCD，

∴∠CAE=∠E，

∴AC=CE，

∴△ACE是等腰三角形．

例4  2.

变式1 连接BC，

∵AB=AC，

∴∠ABC=∠ACB，

又∵∠ABD=∠ACE，

∴∠FBC=∠FCB，

∴FB=FC.

变式2 过B作BG⊥AC于G,

∵BA=BC,

∴∠ABG=∠CBG．

∵DF⊥AC,

∴BG//BF,

∴∠ABG=∠D,∠CBG=∠BED，

∴∠D=∠BED,

∴△DBE是等腰三角形.

变式3 ∵AD平分∠BAC，

∴∠BAD=∠ACD．

又∵AD∥EG，

∴∠G=∠CAD，∠AFG=∠BAD，

∴∠G=∠AFG，∴AG=AF

∴△AGF是等腰三角形．

6. AE∥BC．

∵AB=AC，

∴∠B=∠C．

∵AE平分∠DAC，

∴∠DAE=∠CAE．

又∵∠DAE+∠CAE=∠B+∠C,

∴2∠DAE=2∠B，即∠DAE=∠B，

∴AE∥BC．

7. 设∠B=x，

∵AB=AC，∠B=∠C，AC=CD,∠ADC=∠DAC=2∠B，

∴x+x+3x=180°，解得x=36°，

∴∠ABC =36°.

8．∵AF是△ABC的角平分线, ∠BAC=90°,

∴∠EAD=∠CAD=45°.

∵DE∥AC,

∴∠CAD=∠EAD=45°, ∠BED=90°,

∴AE=DE.

∵BD⊥AF,

∴∠EBD=∠EDB=45°,

∴BE=DE,

∴AE=BE．

9. DE∥AF.

∵△ABC中，AB=AC，AF⊥BC，

∴∠BAF=∠CAF（等腰三角形的三线合一）,

又AD=AE，

∴∠ADE=∠AED（等边对等角）.

又∵∠BAC=∠ADE+∠AED，∠BAC=∠BAF+∠CAF，

∴∠CAF=∠AED，

∴DE∥AF