

初中数学13.3.1 等腰三角形精品第二课时教案
展开13.3.1 等腰三角形(2)
一.教学目标:
1.使学生掌握等腰三角形的判定定理及其推论;
2.掌握等腰三角形判定定理的运用;
3.通过例题的学习,提高学生的逻辑思维能力及分析问题解决问题的能力;
4.通过自主学习的发展体验获取数学知识的感受;
二.教学重点:等腰三角形的判定定理
三.教学难点:性质与判定的区别
教学过程设计
知识回顾
1.等腰三角形的性质是什么?
师生活动:结合幻灯片从角和边两个角度回顾等腰三角形的性质。
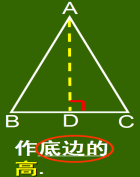
 2.等腰三角形常见辅助线
2.等腰三角形常见辅助线
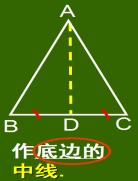
师生活动:教师结合图形提问,学生回忆并回答:作底边的中线,或作底边的高,或作顶角的平分线。
3.怎样的三角形是等腰三角形?还有其它方法可以判断一个三角形是否是等腰三角形吗?
师生活动:教师提问后,学生回答:有两边相等的三角形是等腰三角形.之后教师进一步提出问题:还有其它方法可以判断一个三角形是否是等腰三角形吗?进而引发学生思考,从而引入新课《等腰三角形的判定》
设计意图:让学生通过回忆、思考,复习等腰三角形的性质并通过一个追问引入本节课的新内容.
新课讲授
问题1 你目前拥有的能够判定一个三角形是等腰三角形的方法是什么?
 师生活动:教师提出问题,学生思考可以利用所学过的哪些知识点来解决问题,教师引导写出定义法的几何语言。
师生活动:教师提出问题,学生思考可以利用所学过的哪些知识点来解决问题,教师引导写出定义法的几何语言。
归纳:等腰三角形的判定方法:
1.(定义法)有两边相等的三角形叫等腰三角形.
用符号语言表示为:
在△ABC中,
∵ AC=AB
∴ △ABC为等腰三角形
设计意图:先复习旧知,并以此为根本和基础,学习新知。
 问题2 如图,位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
问题2 如图,位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
师生活动:教师与学生一起结合图形理解题意,并尝试让学生把实际问题转化为数学几何问题。
问题3 如果一个三角形有两条边相等,那么它们所对的角相等。反过来,如果一个三角形有两个角相等,那么它们所对的边有什么关系?同学们先猜想,再试着证明一下.

追问:你是否能够先将猜想转化为几何命题,再进行证明?
求证:如果一个三角形有两个角相等,那么这两个角所对的边也相等.
已知:△ABC中,∠B=C 求证: AB=AC
分析:
1.如何证明两条边相等?
2.如何构造两个全等的三角形?
师生活动:教师提出问题后,先让学生根据理解将问题转化为几何命题,再写出证明过程。在这个环节中,通过巡堂了解学生的证明情况,将不同角度的证明方法通过投影仪在班级里分享讨论以激励学生。
归纳:等腰三角形的判定方法:
2.如果一个三角形有两个角相等, 那么两个角所对的边也相等. (简写成“等角对等边”)
 用符号语言表示为:
用符号语言表示为:
在△ABC中,
∵ ∠B=∠C
∴ AC=AB
则 △ABC为等腰三角形
设计意图:激发学生大胆猜想,接着将猜想转化为几何命题,再进行逻辑推导证明。通过这个训练,学生能基本掌握验证猜想的步骤,并且通过自主证明,更能加深对等腰三角形判定的理解和掌握,
 问题4:等腰三角形的性质与判定有区别吗?
问题4:等腰三角形的性质与判定有区别吗?
师生活动:提问学生,大胆阐述自己的观点,最终引导学生明白等腰三角形的性质和判定为互逆关系。
 问题5:你能用刚学到的新知解决刚才提出的问题了吗?
问题5:你能用刚学到的新知解决刚才提出的问题了吗?
师生活动:请个别学生口述问题2的证明过程,教师在白板上板书。
设计意图:既是对新知的巩固也是课堂上的前后呼应。
课堂练习
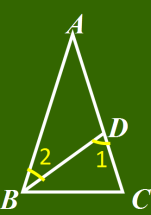
1、如图,∠A =36°,∠DBC =36°,∠C =72°,图中一共有几个等腰三角形?分别计算∠1 ,∠2的度数.
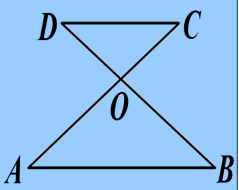 2、如图,AC 和BD 相交于点O,且AB∥DC,OA =OB.
2、如图,AC 和BD 相交于点O,且AB∥DC,OA =OB.
求证:OC =OD.
证明:在ΔOAB中∵OA=OB,
∴∠A=∠B(等边对等角)
∵AB∥DC,
∴∠A=∠C,∠B=∠D.(两直线平行,内错角相等)
∴∠C=∠D (等量代换)
∴OC=OD(等角对等边)
例2 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
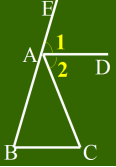 已知:∠CAE是△ ABC的外角,∠1=∠2,AD∥BC.
已知:∠CAE是△ ABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC
证明:∵AD∥BC,
∴∠1=∠B(两直线平行, 同位角相等)
∠2=∠C(两直线平行,内错角相等)
又∵∠1=∠2
∴∠B=∠C
∴AB=AC(等边对等角)
师生活动:给学生一定的时间完成,通过投影仪展示学生的推导过程,强化几何语言的正确表达,
设计意图:以练代讲更能激发学生自主思考,同时还能及时巩固新知,学生存在的问题可以得到及时反馈和解决。
例3 已知等腰三角形底边长为a ,底边上的高的长为h ,求作这个等腰三角形.
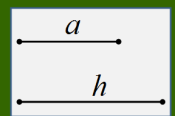 作法:
作法:
(1)作线段AB =a;
(2)作线段AB 的垂直平分线MN,与AB 相交于点D;
(3)在MN上取一点C,使 DC=h;
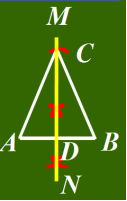 (4)连接AC,BC,则△ABC 就是所求作的等腰三角形.
(4)连接AC,BC,则△ABC 就是所求作的等腰三角形.
师生活动:教师引导学生做出图形,并用所学的定理证明所作的三角形为等腰三角形。
课堂小结
(1)等腰三角形的判定方法有哪几种?
(2)结合本节课的学习,谈谈等腰三角形性质和判定的区别和联系.
设计意图:引导学生从知识内容和学习过程两个方面总结自己的收获,使用问题式的课堂小结模式能够促使学生主动回顾整个课堂的学习过程以及所获的新知识,对课堂有了整体的认识。
 巩固提升
巩固提升
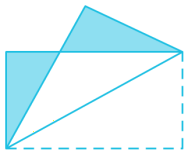
1.如图,把一张长方形的纸沿着对角线折叠,重合部分是一个等腰三角形吗?为什么?
2. 求证:如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形.
设计意图:考查学生对本节课知识的掌握情况,提高拓展能力.
初中数学人教版八年级上册13.3.1 等腰三角形第2课时教案及反思: 这是一份初中数学人教版八年级上册13.3.1 等腰三角形第2课时教案及反思,共6页。教案主要包含了教学目标,教学重难点,教学过程等内容,欢迎下载使用。
初中数学人教版八年级上册13.3.1 等腰三角形第1课时教学设计: 这是一份初中数学人教版八年级上册13.3.1 等腰三角形第1课时教学设计,共7页。教案主要包含了教学目标,教学重难点,教学过程等内容,欢迎下载使用。
数学八年级上册13.3.1 等腰三角形公开课第一课时教案: 这是一份数学八年级上册13.3.1 等腰三角形公开课第一课时教案,共3页。教案主要包含了教学目标,重点难点,教学过程等内容,欢迎下载使用。












