人教版八年级上册13.3.1 等腰三角形获奖教学作业课件ppt

这是一份人教版八年级上册13.3.1 等腰三角形获奖教学作业课件ppt，文件包含1331等腰三角形的性质pptx、1331等腰三角形的性质同步练习解析版docx、1331等腰三角形的性质教学设计docx、1331等腰三角形的性质同步练习原卷版docx、1331等腰三角形的性质导学案docx、两个性质的几何语言1mp4、折纸得到等腰三角形1mp4、探究2演示mp4、等腰三角形各部分名称mp4等9份课件配套教学资源，其中PPT共31页， 欢迎下载使用。

13.3.1 等腰三角形的性质
人教版数学八年级上册
1.理解并掌握等腰三角形的性质.(重点)2.经历等腰三角形的性质的探究过程，能初步运用等腰三角形的性质解决有关问题.(难点)
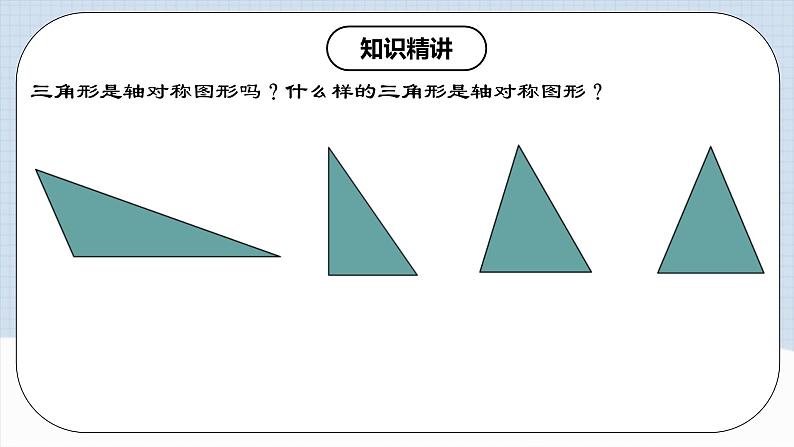
三角形是轴对称图形吗？什么样的三角形是轴对称图形？
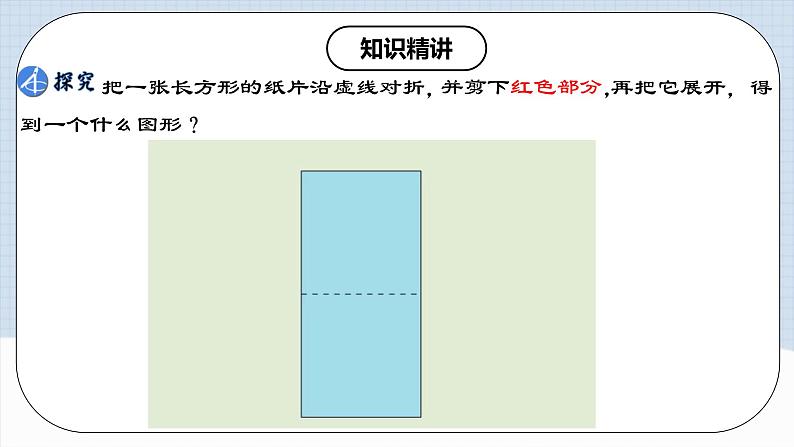
并剪下红色部分，
再把它展开，得到一个什么图形？
把一张长方形的纸片沿虚线对折，
两腰的夹角叫做顶角，
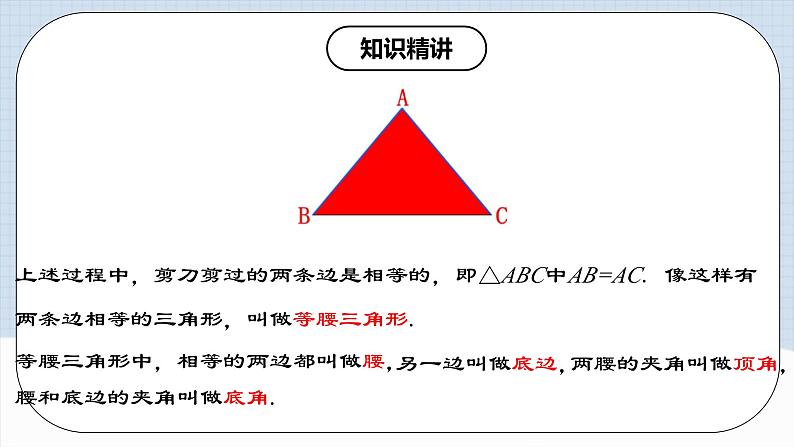
上述过程中，剪刀剪过的两条边是相等的，即△ABC中AB=AC. 像这样有两条边相等的三角形，叫做等腰三角形.
等腰三角形中，相等的两边都叫做腰，
另一边叫做底边，
腰和底边的夹角叫做底角.
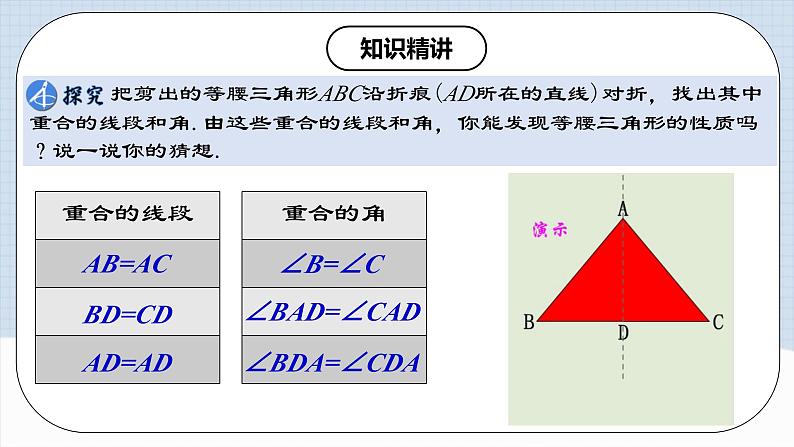
把剪出的等腰三角形ABC沿折痕(AD所在的直线)对折，找出其中重合的线段和角.由这些重合的线段和角，你能发现等腰三角形的性质吗？说一说你的猜想.
AB=AC
BD=CD
AD=AD
∠B=∠C
∠BAD=∠CAD
∠BDA=∠CDA
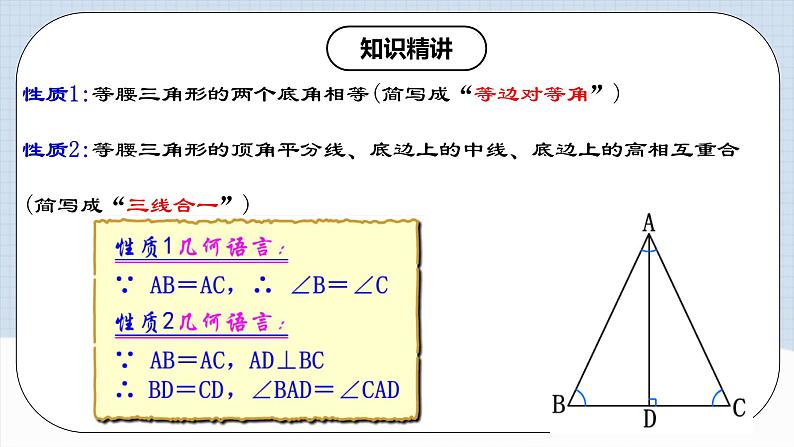
性质1:等腰三角形的两个底角相等(简写成“等边对等角”)性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)
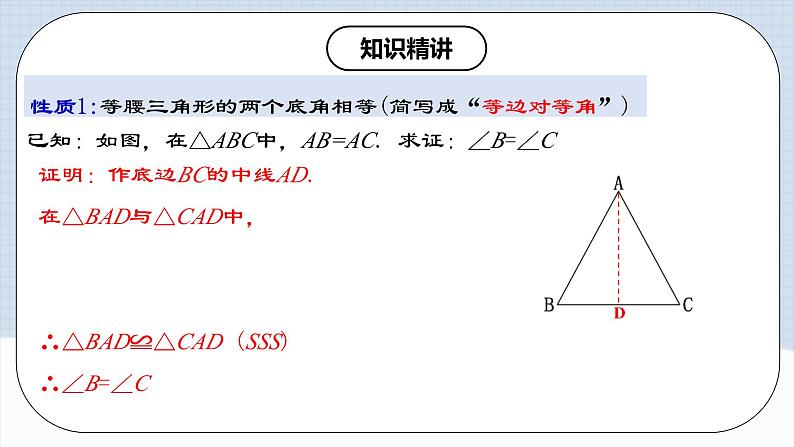
性质1:等腰三角形的两个底角相等(简写成“等边对等角”)
D
证明：作底边BC的中线AD.在△BAD与△CAD中，∴△BAD≌△CAD (SSS)∴∠B=∠C
已知：如图，在△ABC中，AB=AC. 求证：∠B=∠C
由△BAD≌△CAD，还可以得出∠BAD=∠CAD，∠BDA=∠CDA，从而AD⊥BC.这也就证明了等腰三角形ABC底边上的中线AD平分顶角∠BAC并垂直于底边BC.
用类似的方法，还可以证明等腰三角形顶角的平分线平分底边并且垂直于底边，底边上的高平分顶角并且平分底边. 这也就证明了性质2.
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)
性质1:等腰三角形的两个底角相等(简写成“等边对等角”)
D
证明：作底边BC的中线AD.在△BAD与△CAD中，∴△BAD≌△CAD (SSS)∴∠B=∠C
已知：如图，在△ABC中，AB=AC. 求证：∠B=∠C
还有其他的证法吗？
性质1:等腰三角形的两个底角相等(简写成“等边对等角”)
已知：如图，在△ABC中，AB=AC. 求证：∠B=∠C
D
证明：作顶角∠BAC的平分线AD.∴∠BAD=∠CAD在△BAD与△CAD中，∴△BAD≌△CAD (SAS)∴∠B=∠C
性质1:等腰三角形的两个底角相等(简写成“等边对等角”)
已知：如图，在△ABC中，AB=AC. 求证：∠B=∠C
D
证明：过点A作底边BC的高AD.∴∠BDA=∠CDA=90°在Rt△BAD与Rt△CAD中，∴Rt△BAD≌Rt△CAD(HL)∴∠B=∠C
从以上证明也可以得出，等腰三角形底边上的中线的左右两部分经翻折可以重合，等腰三角形是轴对称图形，底边上的中线(顶角的平分线、底边上的高)所在的直线就是它的对称轴.
性质1:等腰三角形的两个底角相等(简写成“等边对等角”)性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)
例1.如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD.求△ABC各角的度数.
解：∵AB=AC，BD=BC=AD∴∠ABC=∠C=∠BDC，∠A=∠ABD (等边对等角)设∠A=x，则∠BDC=∠A+∠ABD=2x从而∠ABC=∠C=∠BDC=2x于是在△ABC中，有∠A+∠ABC+∠C=x+2x+2x=180°解得 x=36°所以，在△ABC中，∠A=36°，∠ABC=∠C=72°
【点睛】在含多个等腰三角形的图形中求角时，常常利用方程思想，通过内角、外角之间的关系进行转化求解.
如图，点D在AC上，点E在AB上，且AB=AC，BC=BD，AD=DE=BE,求∠A的度数.
解:设∠A=x,∵AD=DE=BE ∴∠DEA=∠A=x，∠EBD=∠EDB∵∠DEA=∠EBD+∠EDB ∴∠EBD=∠EDB=0.5x∴∠BDC=∠A+∠ABD=x+0.5x=1.5x∵BC=BD，AB=AC∴∠BDC=∠BCD=∠ABC=1.5x在△ABC中，∠A+∠ABC+∠C=180°即x+1.5x+1.5x=180°解得x=45°，即∠A=45°
 
 
例3.已知:如图，点D、E在△ABC的边BC上,AD=AE，BD=EC.求证: AB=AC.
证法1:∵AD=AE∴∠ADE=∠AED(等边对等角)∵BD=EC∴BD+DE=EC+DE即BE=CD在△ABE和△ACD中∴△ABE≌△ACD(SAS) ∴AB=AC
例3.已知:如图，点D、E在△ABC的边BC上,AD=AE，BD=EC.求证: AB=AC.
证法2:∵AD=AE∴∠ADE=∠AED(等边对等角)∴∠ADB=∠AEC(等角的补角相等)在△ABD和△ACE中，∴△ABD≌△ACE(SAS)∴AB=AC
例3.已知:如图，点D、E在△ABC的边BC上,AD=AE，BD=EC.求证: AB=AC.
证法3:过A作AF⊥BC于F∵AD=AE，AF⊥BC∴DF=EF(等腰三角形“三线合一”)∵BD=EC∴DF+BD=EF+EC即BF=CF∴AF垂直平分BC∴AB=AC
1.等腰三角形的一个角等于20°,则另外两个内角分别为( )A.20°、140° B.20°、140°或80°、80°C.80°、80° D.20°、80°2.等腰三角形中，AB长是BC长2倍，三角形的周长是40，则AB的长为( )A.20 B.16 C.20或16 D.18
B
B
3.如图，在△ABC中，AB=AC，D是BC的中点，∠B=40°，则∠BAD的度数为( )A.100° B.80° C.50° D.40°4.如图，在△ABC中，AB=AC， CD⊥AB于D,则下列判断正确的是( )A.∠A=∠B B.∠A=∠ACDC.∠A=∠DCB D.∠A=2∠BCD
C
D
5.如图，AB//CD， 点E在BC上，CD=CE，∠D=70°，则∠B=_____.6.如图，点D在AC上，AB=BD=CD，∠C=40°，则∠ABD=_____.
40°
20°
7.如图(3)，在△ABC中，AB=AC，AD⊥BC于点D.若AB=6，CD=4,则△ABC的周长是_____.8.如图(4)，是一钢架，∠AOB=10°,为使钢架更加坚固，需在内部添加一些钢管EF、FM、MH……添加的钢管长度都与OE相等，则最多能添加这样的钢管_____根.
8
20
9.如图，在△ABC中，AB=AD=DC，∠BAD=26°.求∠B和∠C的度数.
解：∵AB=AD=DC∴∠B=∠ADB，∠C=∠DAC又∵∠BAD=26°∴∠B=∠ADB=(180°-26°)÷2=77°∴∠C=∠DAC=∠ADB÷2=77°÷2=38.5°
 
 
11.如图，AB＝AC，CA平分∠BCD，E点在BC上，且∠BAC＝∠EAD＝90°．求证：CD＝BE．
证明：∵AB＝AC，∴∠B＝∠ACB，∵CA平分∠BCD，∴∠ACD＝∠ACB，∴∠B＝∠ACD，∵∠BAC＝∠EAD＝90°，∴∠BAE＝∠CAD，在△ABE与△ACD中，∴△BAE≌△CAD（ASA），∴BE＝CD．
 
 
 
 
∴△ADE≌△CGE(AAS)，∴DE=GE，即DG=2DE，又∵点G是BD的中点，∴DG=BG，∴CF=2DE．
性质1:等腰三角形的两个底角相等(简写成“等边对等角”)性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)