






人教A版 (2019)必修 第一册5.7 三角函数的应用授课课件ppt
展开1.会用三角函数解决简单的实际问题.2.可以利用三角函数构建刻画事物周期变化的数学模型.
基础落实·必备知识全过关
重难探究·能力素养全提升
成果验收·课堂达标检测
目 录 索 引
知识点1 函数y=Asin(ωx+φ),x>0(A>0,ω>0)中,各参数的物理意义
又初相为-π,所以相位ωx+φ=3πx-π.
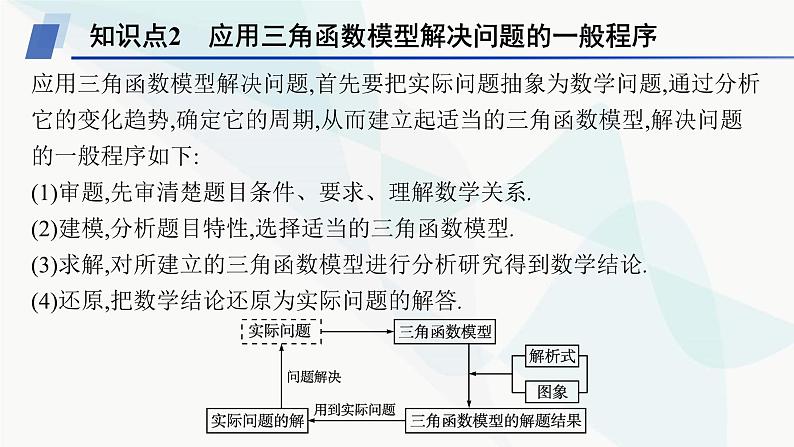
知识点2 应用三角函数模型解决问题的一般程序
应用三角函数模型解决问题,首先要把实际问题抽象为数学问题,通过分析它的变化趋势,确定它的周期,从而建立起适当的三角函数模型,解决问题的一般程序如下:(1)审题,先审清楚题目条件、要求、理解数学关系.(2)建模,分析题目特性,选择适当的三角函数模型.(3)求解,对所建立的三角函数模型进行分析研究得到数学结论.(4)还原,把数学结论还原为实际问题的解答.
过关自诊弹簧振子以O为平衡位置,在B,C两点间做简谐运动,B,C相距20 cm,某时刻振子处在B点位置,经0.5 s振子首次到达C点,求:(1)振动的振幅、周期和频率;(2)弹簧振子在5 s内通过的路程及位移.
解 (1)设振幅为A,则2A=20 cm,所以A=10 cm.设周期为T,则 =0.5 s,所以T=1 s,所以f=1 Hz.(2)振子在0.5 s内通过的路程为20 cm,故在5 s内通过的路程s=5×40=200(cm).5 s末物体处在B点,所以它的位移为0 cm.
探究点一 三角函数模型在物理中的应用
又ω>0,∴ω≥200π.∴正整数ω的最小值为629.
规律方法 三角函数在物理中的应用三角函数模型在物理中的应用主要体现在简谐运动、交流电电流、电压等方面,其中对弹簧振子和单摆的运动等有关问题考查最多,尤其要弄清振幅、频率、周期、平衡位置等物理概念的意义和表示方法.
变式训练1 一单摆从某点开始来回摆动,离开平衡位置的距离s(单位:cm)和时间t(单位:s)之间的函数关系式为s=6sin .(1)当单摆开始摆动(t=0)时,离开平衡位置的距离是多少?(2)当单摆摆动到最右边时,离开平衡位置的距离是多少?(3)单摆来回摆动一次需多长时间?
所以此时离开平衡位置3 cm.(2)离开平衡位置6 cm.
探究点二 三角函数模型在生活中的应用
【例2】 如图为一个观光缆车示意图,该观光缆车半径为4.8 m,圆上最低点与地面距离为0.8 m,60 s转动一圈,图中OA所在直线与地面垂直,以OA为始边,逆时针转动θ角到OB,设点B与地面距离为h m.(1)求h与θ间关系的函数解析式;(2)设从OA开始转动,经过t秒到达OB,求h与t间关系的函数解析式.
解 (1)由题意可作图如图.过点O作地面平行线ON,过点B作ON的垂线BM交ON于点M.
规律方法 解三角函数应用问题的基本步骤
变式训练2 某地昆虫种群数量在七月份1~13日的变化如图所示,且近似满足y=Asin(ωt+φ)+b(A>0,ω>0,|φ|<π).(1)根据图中数据求函数解析式;(2)从7月1日开始,每隔多长时间种群数量就出现一个低谷或一个高峰?
(2)由图可知,每隔半周期种群数量就出现一个低谷或高峰,
∴从7月1日开始,每隔6天,种群数量就出现一个低谷或一个高峰.
探究点三 数据拟合三角函数模型问题
【例3】 已知某海滨浴场的海浪高度y(单位:米)是时间t(单位:时)的函数,其中0≤t≤24,记y=f(t),下表是某日各时的浪高数据:
经长期观测,y=f(t)的图象可近似地看成是函数y=Acs ωt+b的图象.(1)根据表中数据,求其最小正周期T、振幅A及函数解析式;(2)假设当海浪高度大于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的8:00到20:00之间,有多少时间可供冲浪爱好者进行活动?
又0≤t≤24,所以0≤t<3或9
即12k-2
本节要点归纳1.知识清单:(1)三角函数在物理中的应用.(2)三角函数在生活中的应用.2.方法归纳:数学建模(拟合)、数形结合.3.常见误区:选择三角函数模型时,最后结果忘记回归实际进行检验.
2.(多选题)如图所示是一质点做简谐运动的图象,则下列结论正确的是( )A.该质点的运动周期为0.8 sB.该质点的振幅为5 cmC.该质点在0.1 s和0.5 s时运动速度最大D.该质点在0.1 s和0.5 s时运动速度为0 cm/s
解析 由题图可知, =0.7-0.3=0.4,所以T=0.8;最小值为-5,所以振幅为5 cm;在0.1 s和0.5 s时,质点到达运动的端点,所以速度为0 cm/s.
3.交流电的电压U(单位:V)与时间t(单位:s)的关系可用U= 来表示,则电压的最大值是 V,第一次获得这个最大值的时间是 s.
4.海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表:
(1)已知该港口的水深y与时间x满足函数y=Acs(ωx+φ)+b(A>0,ω>0,b>0,-π<φ<π),画出函数图象,并求出函数解析式.(2)现有一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的间隙(船底与洋底的距离),该船何时能进入港口?在港口能待多久?
解 (1)图象如下:
必修 第一册5.7 三角函数的应用作业ppt课件: 这是一份必修 第一册5.7 三角函数的应用作业ppt课件,共18页。PPT课件主要包含了ABD等内容,欢迎下载使用。
人教A版 (2019)必修 第一册5.7 三角函数的应用集体备课ppt课件: 这是一份人教A版 (2019)必修 第一册5.7 三角函数的应用集体备课ppt课件,共29页。PPT课件主要包含了目录索引等内容,欢迎下载使用。
高中人教A版 (2019)5.7 三角函数的应用作业课件ppt: 这是一份高中人教A版 (2019)5.7 三角函数的应用作业课件ppt,共21页。













