初中数学苏科版八年级上册3.3 勾股定理的简单应用同步练习题

3.3勾股定理的简单应用提升练习-苏科版数学八年级上册

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．如图，一圆柱高，底面半径，一只蚂蚁从点爬到点处吃食，要爬行的最短路程（取3）是（    ）

A． B． C． D．无法确定

2．如图，一架5米长的梯子，斜靠在一堵竖直的墙上，这时梯顶A距地面4米，若梯子沿墙下滑1米，则梯足B外滑（　　）米

A．0.6 B．0.8 C．1 D．2

3．《九章算术》勾股章有一个问题，其意思是：现有一竖立着的木柱，在木柱上端系有绳索，绳索从木柱上端顺木柱下垂后，堆在地面的部分尚有3尺，牵着绳索退行，在离木柱根部8尺处时绳索用尽，请问：绳索有多长？若设绳索长x尺，根据题意，可列方程为（　　）

A． B．

C． D．

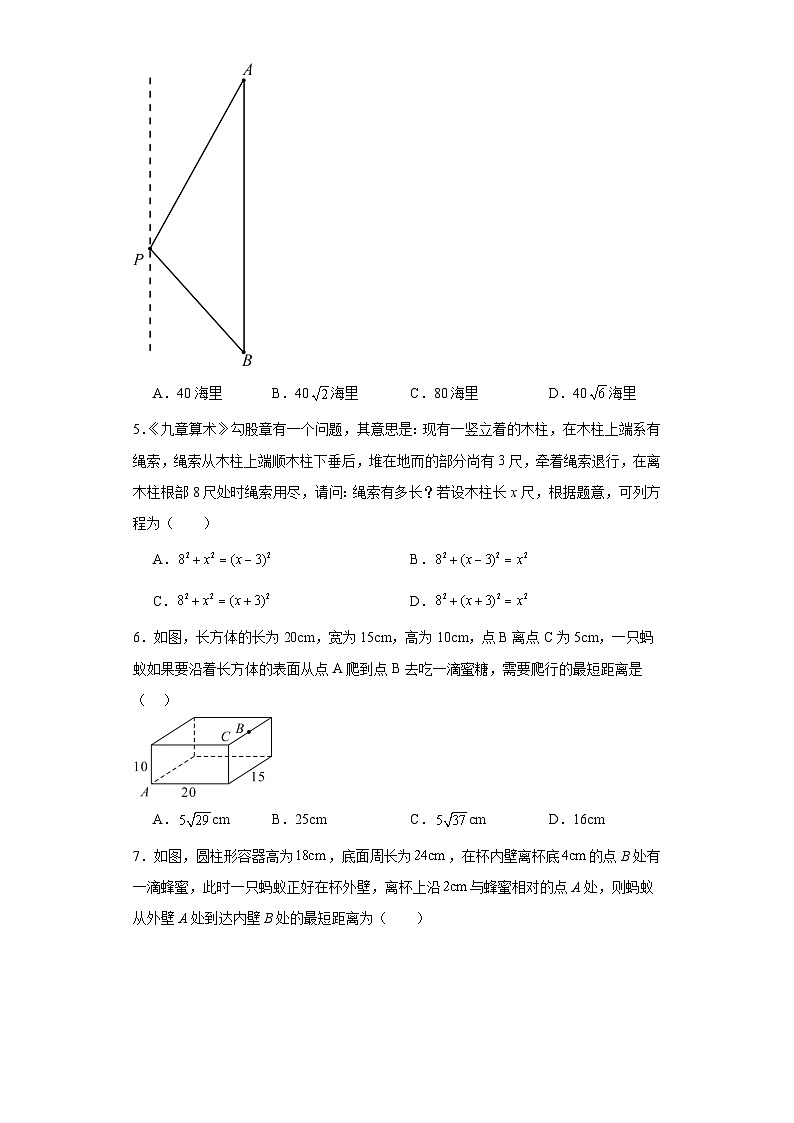
4．如图，一艘海轮位于灯塔P的北偏东30°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处与灯塔P的距离为（　　）

A．40海里 B．40海里 C．80海里 D．40海里

5．《九章算术》勾股章有一个问题，其意思是：现有一竖立着的木柱，在木柱上端系有绳索，绳索从木柱上端顺木柱下垂后，堆在地而的部分尚有3尺，牵着绳索退行，在离木柱根部8尺处时绳索用尽，请问：绳索有多长？若设木柱长x尺，根据题意，可列方程为（　　）

A． B．

C． D．

6．如图，长方体的长为20cm，宽为15cm，高为10cm，点B离点C为5cm，一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖，需要爬行的最短距离是（    ）

A．cm B．25cm C．cm D．16cm

7．如图，圆柱形容器高为，底面周长为，在杯内壁离杯底的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿与蜂蜜相对的点A处，则蚂蚁从外壁A处到达内壁B处的最短距离为（　　）

A． B． C． D．

8．如图，透明的圆柱形容器（容器厚度忽略不计）的高为，底面周长为，在容器内壁离容器底部的点B处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿的点A处，则蚂蚁吃到饭粒需爬行的最短路径是（    ）

A． B． C． D．

9．一只螳螂在一圆柱形松树树干的点处，它发现在其正上方的点处有一只小虫子，螳螂想捕到这只虫子，但又怕被发现，于是按如图所示的路线，绕到虫子后面吃掉它．已知树干的底面周长为，，两点间的距离为，则螳螂绕行的最短路程为（    ）.

A． B． C． D．

10．一云梯AB长25米，如图那样斜靠在一面墙上，云梯底端离墙7米，如果云梯的顶端下滑了4米，那么它的底端在水平方向滑动BB'的长是（　　）

A．10米 B．8米 C．6米 D．4米

二、填空题

11．某工程队负责挖掘一处通山隧道，为了保证山脚A，B两处出口能够直通，工程队在工程图上留下了一些测量数据（此为山体俯视图，图中测量线拐点处均为直角，数据单位：米）．据此可以求得该隧道预计全长      米．

12．轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行，在B处观测灯塔A位于南偏东75°方向上，轮船航行半小时到达C处，在C处观测灯塔A位于北偏东60°方向上，则B处与灯塔A的距离是          海里．

13．如图，一根竖直的木杆在离地面3.1处折断，木杆顶端落在地面上，且与地面成38°角，则木杆折断之前高度约为          ．（参考数据：）

14．如图，某宾馆在重新装修后，准备在大厅的主楼梯上铺上红色地毯(地毯宽与楼梯宽一样），则所铺地毯的长为       米．

15．如图，圆柱的高为，底面圆的周长为，一只蚂蚁从下底面的点A处沿圆柱侧面爬到上底面与点A相对的点B处觅食，则蚂蚁爬行的最短路程为     

16．如图 ，在中， ，，点、为 边上两点， 将、分别沿、折叠，、两点重合于点，若，则的长为          ．

17．长、宽、高分别为4cm、3cm、12cm的长方体纸盒内可完全放入的棍子最长是          cm．

18．圆柱的轴截面ABCD是边长为4的正方形，动点P的初始位置在AB上，，点P由此出发，沿着圆柱的侧面移动到CD的中点S，点P与点S之间的最短距离是      ．（π取3）

19．如图，是一个两级台阶，它的每一级的长、宽、高分别为A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁从A点沿着台阶面爬到B点的最短路程是        m ．

20．在平静的湖面上，有一支红莲，高出水面1米，阵风吹来，红莲被吹到一边，花朵齐及水面，已知红莲移动的水平距离为3米，问这里水深是        m.

三、解答题

21．“儿童散学归来早，忙趁东风放纸鸢”，又到了放风筝的最佳时节．某校八年级某班的小明和小亮学习了“勾股定理”之后，为了测得风筝的垂直高度CE，他们进行了如下操作：①测得水平距离BD的长为12米；②根据手中剩余线的长度计算出风筝线BC的长为20米；③牵线放风筝的小明的身高为1.7米．

(1)求风筝的垂直高度CE；

(2)如果小明想风筝沿CD方向下降7米，则他应该往回收线多少米？

22．如图，一个底面为正方形的无盖长方形盒子的长、宽、高分别为，，，即，，现在顶点处有一滴蜜糖，一只蚂蚁如果要沿着长方体的表面从顶点爬到处去吃蜜糖，求需要爬行的最短距离．（注：底面可以爬行）

23．如图，在倾斜角为（即）的山坡上有一棵树，由于大风，该树从点E处折断，其树顶B恰好落在另一棵树的根部C处，已知， ．

(1)求这两棵树的水平距离；

(2)求树的高度．

24．如图，某自动感应门的正上方A处装有一个感应器，离地面距离AB＝2.6米，当人体进入感应器的1.5m及1.5m以内感应范围内时，感应门就会自动打开．小明（CD）身高1.7米缓慢走向感应门，求他走到离感应门多远距离时，门刚好自动打开？

25．读诗求解“ 出水3尺一红莲，风吹花朵齐水面 ，水面移动有6尺，求水深几何请你算”．

参考答案：

1．A

2．C

3．B

4．B

5．C

6．B

7．C

8．A

9．B

10．B

11．1000

12．

13．8.1m

14．7

15．10

16．3 或2

17．13

18．

19．1.7

20．4

21．(1)17.7米

(2)5米

22．蚂蚁爬行的最短距离为

23．(1)3m

(2)6m

24．1.2米

25．4.5 尺