初中数学第三章 勾股定理3.3 勾股定理的简单应用课文配套ppt课件

这是一份初中数学第三章 勾股定理3.3 勾股定理的简单应用课文配套ppt课件，共11页。

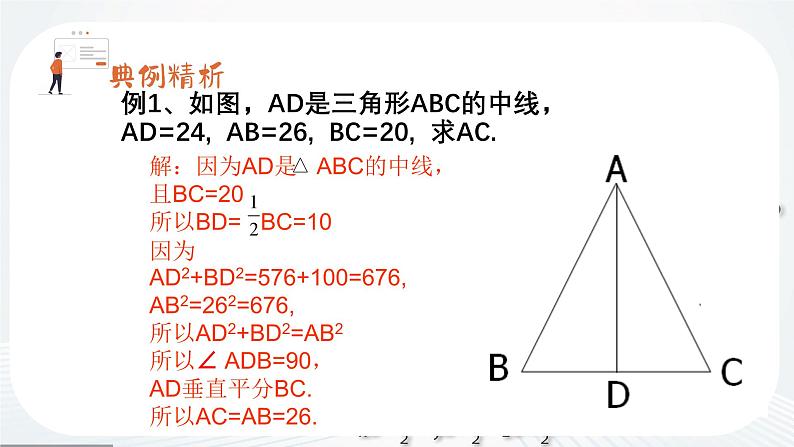
例1、如图，AD是三角形ABC的中线，AD=24, AB=26, BC=20, 求AC.
例2、《九章算数》中有一道“折竹”问题：“今有竹高一丈，末折抵地，去根三尺，问折者高几何？”题意是：一根竹子原高一丈（一丈=10尺），中部有一处折断，竹梢触地面处离竹根三尺，试问折断处离地面多高？
设AC=x尺，则AB=(10-x）尺在Rt ABC中，BC2+AC2=AB2x2+32=(10-x)2解得x=4.55所以折断处离地面4.55尺
变式：有一架秋千，当它静止时，踏板离地的垂直高度DE=0.5m ，将它往前推送 2m（水平距离BC=2m ）时，秋千的踏板离地的垂直高度BF=1.5m ，秋千的绳索始终拉得很直，求绳索 AD的长度．
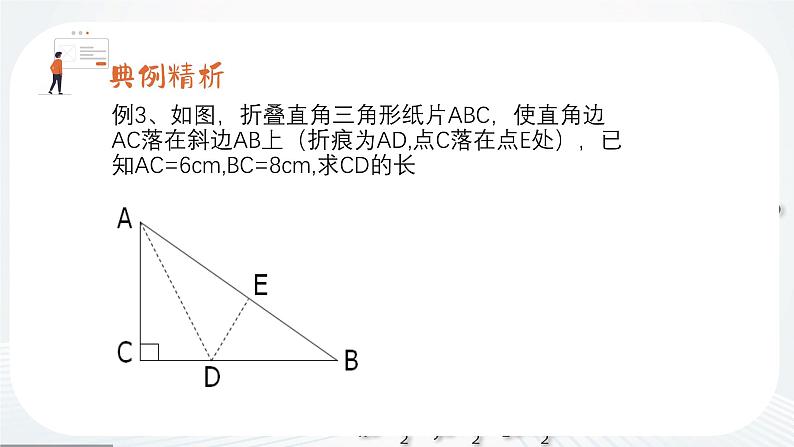
例3、如图，折叠直角三角形纸片ABC，使直角边AC落在斜边AB上（折痕为AD,点C落在点E处），已知AC=6cm,BC=8cm,求CD的长
变式如图，长方形ABCD中，AB＝3cm，AD＝9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（　　）A.3 cm2 B.4 cm2 C.6 cm2 D.12 cm2
例4、如图,一架长为25m的梯子AB斜靠在墙上,梯子的顶端距地面的垂直距离为24m.如果梯子的顶端下滑9m,那么它的底端是否也滑动9 m?
例5，如图, 在△ABC中, AB=15, AC=13, AD是BC上的高, AD=12, 求△ABC的周长和面积．
3.如图, 在△ABC中, AB=15, AC=13, AD是BC上的高, AD=12, 求△ABC的周长和面积．
例6、我国古代有这样一道数学问题：如图，把枯木看作一个圆柱体，因一丈是十尺，则该圆柱的高为20尺，底面周长为3尺，有葛藤自点A处缠绕而上，绕五周后其末端恰好到达点B处，则葛藤的最短长度是_____尺.