2022-2023学年吉林省白城市洮南市第一中学高二下学期期中数学试题含答案

2022-2023学年吉林省白城市洮南市第一中学高二下学期期中数学试题

一、单选题

1．数列，则该数列的第n项为（    ）

A． B． C． D．

【答案】D

【分析】通过数列的规律总结出数列的第n项即可

【详解】设该数列为，

则

以此类推可得，

故选：D

2．设为可导函数，且满足，则函数在处的导数为（    ）

A． B．1 C．1或 D．以上答案都不对

【答案】A

【分析】由，代入即可求解.

【详解】由题意，函数在处的导数为：

.

故选：A.

3．已知函数，则（    ）

A． B． C． D．

【答案】D

【分析】求出导函数，代入，从而求出，，求出.

【详解】因为，所以，

则，所以，则，所以．

故选：D

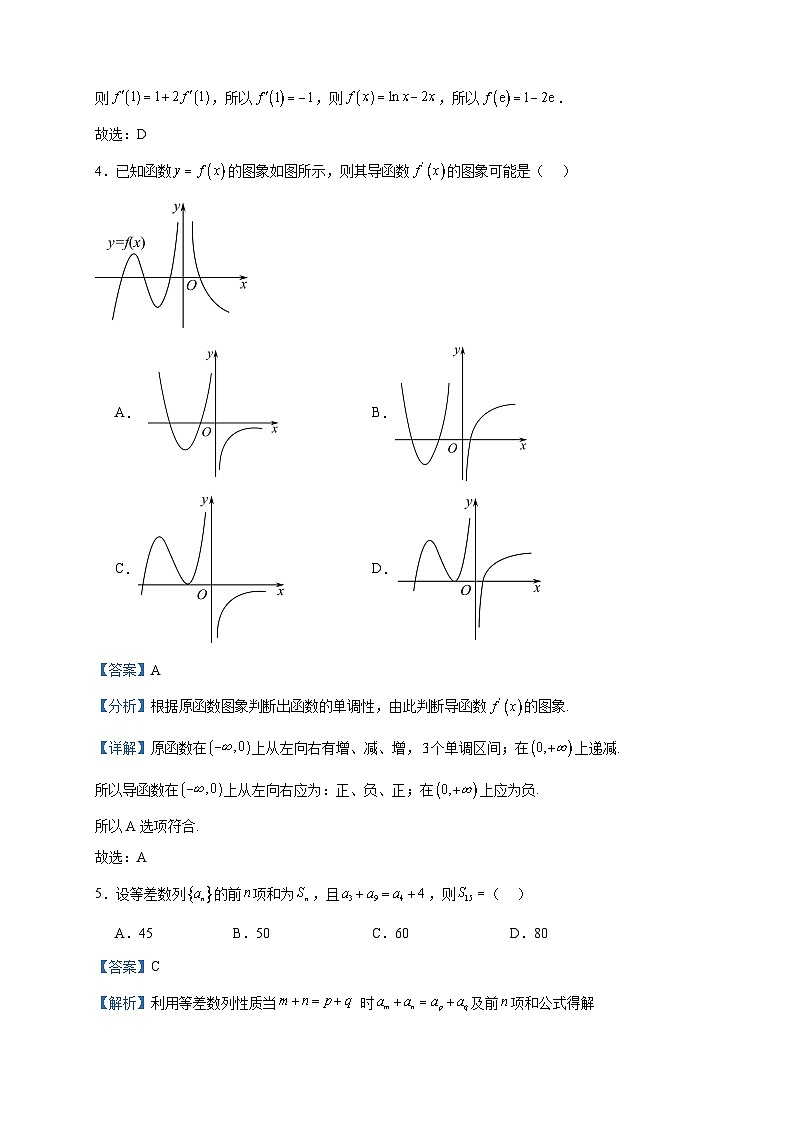
4．已知函数的图象如图所示，则其导函数的图象可能是（   ）

A． B．

C． D．

【答案】A

【分析】根据原函数图象判断出函数的单调性，由此判断导函数的图象.

【详解】原函数在上从左向右有增、减、增，个单调区间；在上递减.

所以导函数在上从左向右应为：正、负、正；在上应为负.

所以A选项符合.

故选：A

5．设等差数列的前项和为，且，则（    ）

A．45 B．50 C．60 D．80

【答案】C

【解析】利用等差数列性质当 时及前项和公式得解

【详解】是等差数列，，，

故选：C

【点睛】本题考查等差数列性质及前项和公式，属于基础题

6．已知是函数图象上的点，则点P到直线的最小距离为(　　)

A． B． C． D．

【答案】D

【分析】在函数的图像上，利用导数求得一点，使得在该点切线的斜率为，再由点到直线距离公式求得最小距离.

【详解】直线2x－y－3＝0的斜率为，令，解得，故，到直线2x－y－3＝0的距离为，故选D.

【点睛】本小题主要考查曲线上的点到直线的距离的最小值的求法，属于基础题.

7．公元前四世纪，毕达哥拉斯学派对数和形的关系进行了研究，他们借助几何图形（或格点）来表示数，称为形数，形数是联系算数和几何的纽带，下图为五角形数的前4个，现有如下说法：

①记所有的五角形数从小到大构成数列，则；

②第9个五角形数比第8个五角形数多25；

③前8个五角形数之和为288；

④记所有的五角形数从小到大构成数列，则的前20项和为610；则正确的个数为（    ）

A．1 B．2 C．3 D．4

【答案】C

【分析】根据图形得到，利用累加法得到，数列为等差数列，计算对比每个选项得到答案.

【详解】根据图形知：，，故①正确；

则

.

，故②正确；

，故③正确；

，数列是首项为1公差为的等差数列，前20项和为，故④错误.

故选：C.

8．已知实数，，函数在上单调递增，则实数的取值范围是（    ）

A． B．

C． D．

【答案】A

【分析】根据指数函数的单调性，结合导数与单调性的关系，通过构造函数进行求解即可.

【详解】解：∵函数在上单调递增，

∴当时，有；

当时，恒成立，

令，，则，

∵，∴，即在上单调递增，∴，

要使当时恒成立，则，解得.

∵函数在上单调递增，∴还需要满足，即，

综上，的取值范围是.

故选：A.

【点睛】关键点睛：本题的关键是除了考虑每段函数是单调递增，还要考虑不等式成立这一条件.

二、多选题

9．已知，且，则a的值为（    ）

A．-3 B．-1 C． D．

【答案】AB

【分析】对复合函数求导，代入,即可求解.

【详解】，

则，解得或.

故选:AB.

10．设等比数列的公比为q，前n项积为，并且满足条件，，，则下列结论正确的是（    ）

A． B．

C．的最大值为 D．

【答案】AC

【分析】通过分析得，根据，则得，结合，可得，再逐步分析，即可判断各选项.

【详解】对A，若，因为，所以，，则与矛盾，

若，因为，所以，，则，与矛盾，

所以，故A正确；

对B，，，，即，

因为，则，所以，故B错误；

对C，由，故C正确；

对D，，故D错误．

故选：AC.

11．已知函数在处有极值，且极值为8，则（    ）

A．有三个零点

B．

C．曲线在点处的切线方程为

D．函数为奇函数

【答案】AC

【分析】由条件根据极值与导数的关系求，判断B，利用导数分析函数的单调性，结合零点存在性定理判断A，根据导数的几何意义求切线，判断C，根据奇函数的定义判断D.

【详解】由题意得，又，又，解得(舍去）或，故B项错误；

，，

当时，，单调递增，

当时，，单调递减，

当时，，单调递增，

又，，，，

所以有三个零点，故A项正确；

又，，

则曲线在点处的切线方程为，即，故C项正确；

，故D项错误.

故选：AC.

12．已知，且，则下列不等关系成立的是（    ）

A． B． C． D．

【答案】ABC

【分析】利用基本不等式易知选项AB正确；利用对数运算法则和重要不等式可知C正确；将不等式化简整理可得，构造函数利用函数单调性即可证明D错误.

【详解】由基本不等式可知，，当且仅当时，等号成立，即A正确；

易知，当且仅当时，等号成立，即B正确；

由重要不等式和对数运算法则可得：

，当且仅当且仅当时，等号成立，即C正确；

由可得，所以，

若，即证明，即

即需证明，

令函数，则，

当时，，即在上单调递增，

所以时，解不等式可得即可，即时不等式成立；

当时，，即在上单调递减，解不等式可得，即时不等式才成立；

综上可知，当时，不等式才成立，所以D错误.

故选：ABC

三、填空题

13．函数的单调递减区间为      ．

【答案】/

【分析】求导，再令即可得解.

【详解】函数的定义域为，

，

令，得，

所以函数函数的单调递减区间为.

故答案为：.

14．若函数在区间内存在最大值，则实数的取值范围是      ．

【答案】

【分析】由题意，求导确定函数的单调性，从而作出函数的简图，由图象求实数的取值范围．

【详解】由题意，，

令，解得或，令，解得，

故在，上是减函数，在上是增函数，

作其图象如下图，

所以当时，取得最大值为，

令，解得，或，

则结合图象可知，

，

解得，,．

故答案为：．

15．关于函数，若函数有三个零点，则实数k的取值范围是      .

【答案】

【分析】作出函数图象，将函数零点转化为方程的根，结合函数图象即可得实数的取值范围.

【详解】因为，所以，令得，

令得或，所以函数的增区间为，减区间为和，

所以函数的极大值为，函数的极大值为，

又当x趋向负无穷大时，无限趋向正穷大，当x趋向正无穷大时，无限趋向于0，

作出函数图象如下：

故函数有三个零点即方程的根有三个，

结合函数图象即可得，故实数的取值范围是.

故答案为：.

16．已知函数为定义在R上的偶函数，当时，，，则不等式的解集是      ．

【答案】

【分析】构造函数，求导分析的单调性，由奇偶性的定义可得为偶函数，不等式，可化为，分类讨论，即可得出答案．

【详解】当时，，即，

设，则当时，，

函数在上单调递增，且，

又是定义在R上的偶函数，有，

则，所以是定义在R上的偶函数，

则有在上单调递减，且，

不等式整理得，

可得，即，

当时，，则或，解得或，

又，所以；

当时，，则，解得，

又，所以；

当时，显然不等式不成立；

综上所述，不等式的解集为，

故答案为：．

四、解答题

17．已知函数，在处的切线方程是，其中是自然对数的底数.

（1）求实数，的值；

（2）求函数的极值.

【答案】（1）；（2）极大值1；无极小值..

【分析】（1）计算，，根据函数在处的切线方程，简单计算可得结果.

（2）根据（1）的结论，可得，然后利用导数，判断原函数的单调性，找到极值点，最后计算可得结果.

【详解】（1）由，得，

由在处的切线方程是，知切点为，斜率为，

所以，

解之得．

（2），，令，得，

由表可知，当时，取得极大值1；无极小值.

【点睛】本题查函数在某点处的切线方程求参数以及求具体函数的极值，理解函数在某点处导数的几何意义以及掌握导函数与原函数的关系，属基础题.

18．已知函数.

(1)当时，求曲线上在点处的切线方程；

(2)若在上单调递减，求实数m的取值范围.

【答案】(1)

(2)

【分析】（1）求导，再根据导数的几何意义即可得解；

（2）求导，在上单调递减，则在上恒成立，分离常数得在上恒成立，构造函数，求出其最小值即可.

【详解】（1）当时，，

则，

则，

所以曲线上在点处的切线方程为；

（2），

因为在上单调递减，

所以在上恒成立，

即在上恒成立，

令，

因为在上都是减函数，

所以函数在上是减函数，

所以，

所以.

19．一艘轮船在航行中每小时的燃料费p和它的速度x的立方成正比.已知速度为每小时10海里时，燃料费是每小时6元，而其他与速度无关的费用是每小时96元，现轮船航行1海里：

(1)将该轮船所需的总费用y元表示为轮船的速度x海里/小时的函数；

(2)轮船的速度多少时，所需的费用总和最小？

【答案】(1)

(2)20

【分析】（1）根据条件先求出p的解析式，再求出y的解析式；

（2）运用基本不等式求解.

【详解】（1）设每小时的燃料费用，则，由题意：航行1海里的时间为小时，

（）；

（2）由（1）：，

当且仅当，即时，等号成立，即当时，y取得最小值；

综上，总费用，当时，所需的费用总和最小.

20．在条件：①；②且；③且中任选一个，补充在横线上，并求解下面问题：已知数列的前项和为___________，

(1)求数列的通项公式；

(2)数列的前项和为，求

【答案】(1)

(2)

【分析】（1）选①直接利用，再对进行检验即可，选②或③通过化简得到，再利用累乘法得到；

（2），再进行裂项求和即可.

【详解】（1）若选①，由，①

时，，②

①②

而也满足上式，

若选②，①

时，，②

①②

.

若选③，①

时，，②

①②

时由①知也满足上式，，

当时， ，

.

（2）此时，

.

21．已知函数.

(1)讨论函数的单调性；

(2)若函数有最小值，记为，关于的方程有三个不同的实数根，求实数的取值范围.

【答案】(1)当时，在上单调递减；当时，在上单调递减，在上单调递增；

(2).

【分析】（1）函数求导得，分和两种情况讨论即可；

（2）结合（1）中的单调性可得最值，即，令，然后利用导数研究函数的性质即得.

【详解】（1）∵，

∴，，

当时，，所以在上单调递减；

当时，，

由可得，由可得，

所以在上单调递减，在上单调递增；

综上，当时，在上单调递减；当时，在上单调递减，在上单调递增；

（2）由（1）知，，，即，

方程，即，

令，则，

由可得，由可得，

∴在和上单调递增，在上单调递减，

，，

依题意得.

【点睛】已知函数有零点求参数常用的方法和思路：

（1）直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；

（2）分离参数法：先将参数分离，转化成函数的值域问题解决；

（3）数形结合法：先对解析式变形，在同一个平面直角坐标系中，画出函数的图像，然后数形结合求解.

22．已知函数，为自然对数的底数.

(1)当 且 时，求的最小值；

(2)若函数在上存在极值点，求实数的取值范围.

【答案】(1)

(2)

【分析】（1）根据导数的正负即可判断函数的的单调性，进而可以求函数的最小值；

（2）通过分类讨论的范围，研究函数的导数的正负，进而研究其单调性和极值即可求解.

【详解】（1）证明：当时，，则，

当时，，则,又因为，

所以当时，，仅时，，

所以在上是单调递减，

所以，即.

（2）可得，因为，所以,

①当时，恒成立，所以在上单调递增，没有极值点，

②当时，易知在上单调递增，

因为

当时，，

所以在上单调递减，没有极值点；

当时，，所以存在使，

当时，时，，

所以在处取得极小值，为极小值点.

综上可知，若函数在上存在极值点，则实数.