人教版八年级上册12.3 角的平分线的性质课后复习题

这是一份人教版八年级上册12.3 角的平分线的性质课后复习题，文件包含八年级数学上册专题05两内角平分线求角原卷版docx、八年级数学上册专题05两内角平分线求角解析版docx等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。


专题05 两内角平分线求角

类型一 三角形两内角平分线求角
1．如图，中，，分别是，的平分线，，则等于（       ）

A． B． C． D．
【答案】B
【解析】
【分析】
根据三角形的内角和定理求出∠ABC+∠ACB的度数，再根据角平分线的定义求出∠OBC+∠OCB的度数，再根据三角形的内角和定理即可求出∠BOC的度数．
【详解】
解：∵∠A=50°，
∴∠ABC+∠ACB=180°-∠A=180°-50°=130°，
∵BO，CO分别是∠ABC，∠ACB的平分线，
,

∴∠BOC=180°-（∠OBC+∠OCB）=180°-65°=115°．
故选：B．
【点睛】
本题考查角平分线的有关计算，三角形内角和定理．本题中是将∠OBC+∠OCB看成一个整体求得的，掌握整体思想是解决此题的关键．
2．如图所示，AC⊥BC，AO，BO 分别是 ∠A，∠B 的平分线，且相交于点 O，则 ∠AOB 等于（          ）

A． B． C． D．
【答案】A
【解析】
【分析】
根据角平分线的定义得到∠OAB+∠OBA=∠CAB+∠ABC=45°，再利用三角形内角和定理即可求解．
【详解】
解：∵AC⊥BC，
∴∠C=90°，
∴∠CAB+∠ABC=90°，
∵AO，BO 分别是 ∠A，∠B 的平分线，且相交于点 O，
∴∠OAB=∠CAB，∠OBA=∠ABC，
∴∠OAB+∠OBA=∠CAB+∠ABC=45°，
在△OAB中，∠AOB=180°-(∠OAB+∠OBA)= 180°-45°=135°，
故选：A．
【点睛】
本题考查了角平分线的定义，三角形内角和定理，熟记各图形的性质并准确识图是解题的关键．
3．如图，在中，平分，平分，若，则的度数为（       ）


A． B． C． D．
【答案】B
【解析】
【分析】
根据BD平分∠ABC，CD平分∠BCA，可以得到，，再根据三角形内角和定理和进行求解即可.
【详解】
解：∵BD平分∠ABC，CD平分∠BCA，
∴，，
∵，，
∴，，
∵，
∴，
∴，
∴，
故选B.


【点睛】
本题主要考查了三角形内角和定理，角平分的性质，解题的关键在于能够熟练掌握相关知识进行求解.
4．如图，△ABC的角平分线BD与CE交于点O，若∠COD＝50°，则∠BAC的度数是__________．

【答案】80°
【解析】
【分析】
依据三角形外角性质，即可得到∠OBC+∠OCB=50°，再根据△ABC的角平分线BD，CE相交于点O，可得∠ABC+∠ACB=2（∠OBC+∠OCB）=100°，最后根据三角形内角和定理，即可得到△ABC中，∠A=80°．
【详解】
解：∵∠COD=50°，
∴∠OBC+∠OCB=50°，
∵△ABC的角平分线BD，CE相交于点O，
∴∠ABC+∠ACB=2（∠OBC+∠OCB）=100°，
∴△ABC中，∠BAC=80°，
故答案为：80°．
【点睛】
本题主要考查了三角形内角和定理的运用和三角形外角的性质，能结合定理正确识图，得出相应角之间的关系是解题关键．
5．如图，在△ABC中，∠ABC和∠ACB的平分线相交于点P．
（1）若∠ABC+∠ACB＝130°，求∠BPC的度数．
（2）当∠A为多少度时，∠BPC＝3∠A？

【答案】（1）；（2）
【解析】
【分析】
（1）根据角平分线的定义，求得，，再根据三角形内角和定理即可求得；
（2）根据（1）的方法求得，再结合条件∠BPC＝3∠A，解方程即可求得∠A．
【详解】
（1）平分，平分，
，
∠ABC+∠ACB＝130°，
，
，
（2）平分，平分，
，
，
，
，



∠BPC＝3∠A
，
．
【点睛】
本题考查了与角平分线有关的角度计算，三角形内角和定理，掌握三角形内角和定理是解题的关键．
6．如图，在△ABC中，∠ABC和∠ACB的平分线相交于点P，根据下列条件，求∠BPC的度数．
（1）若∠ABC＝50°，∠ACB＝60°，则∠BPC＝　 　；
（2）若∠ABC+∠ACB＝120°，则∠BPC＝　 　；
（3）若∠A＝80°，则∠BPC＝　 　；
（4）从以上的计算中，你能发现已知∠A，求∠BPC的公式是：∠BPC＝　 　（提示：用∠A表示）．

【答案】（1）125°；（2）120°；（3）130°；（4）90°+∠A．
【解析】
【分析】
（1）由∠ABC＝50°，∠ACB＝60°，∠2+∠4=25°+30°＝55°，在△BCP中，由三角形内角和为180°可得答案；
（2）同理，由ABC+∠ACB＝120°，∠ABC和∠ACB的平分线相交于点P，可得∠2+∠4＝×120°＝60°，在△BCP中，由三角形内角和为180°可得答案；
(3) A＝80°，可得ABC+∠ACB＝100°，∠2+∠4＝×100°＝50°，可得∠BPC的度数；
（4）ABC+∠ACB＝180°﹣∠A，∠ABC和∠ACB的平分线相交于点P，可得∠2+∠4＝×（180°﹣∠A），在△BCP中，∠P＝180°﹣×（180°﹣∠A）＝90°+∠A
【详解】
解：（1）∵∠ABC＝50°，∠ACB＝60°，∠ABC和∠ACB的平分线相交于点P，
∴∠2+∠4＝25°+30°＝55°，
∴△BCP中，∠P＝180°﹣55°＝125°，
故答案为125°；
（2）∵∠ABC+∠ACB＝120°，∠ABC和∠ACB的平分线相交于点P，
∴∠2+∠4＝×120°＝60°，
∴△BCP中，∠P＝180°﹣60°＝120°，
故答案为120°；
（3）∵∠A＝80°，
∴∠ABC+∠ACB＝100°，
∠ABC和∠ACB的平分线相交于点P，
∴∠2+∠4＝×100°＝50°，
∴△BCP中，∠P＝180°﹣50°＝130°，
故答案为130°；
（4））∵∠ABC+∠ACB＝180°﹣∠A，∠ABC和∠ACB的平分线相交于点P，
∴∠2+∠4＝×（180°﹣∠A），
∴△BCP中，∠P＝180°﹣×（180°﹣∠A）＝90°+∠A．
故答案为90°+∠A．
【点睛】
本题主要考查三角形的内角和定理与角平分线的性质： 三角形的内角和是180, 得到相应规律是: 三角形两个内角平分线所夹的钝角等于90+第三个角的一半.
类型二 多边形两内角平分线求角
7．如图，在四边形ABCD中，∠A＝150°，∠C＝60°，∠ABC与∠ADC的平分线交于点O，则∠BOD的度数为（       ）

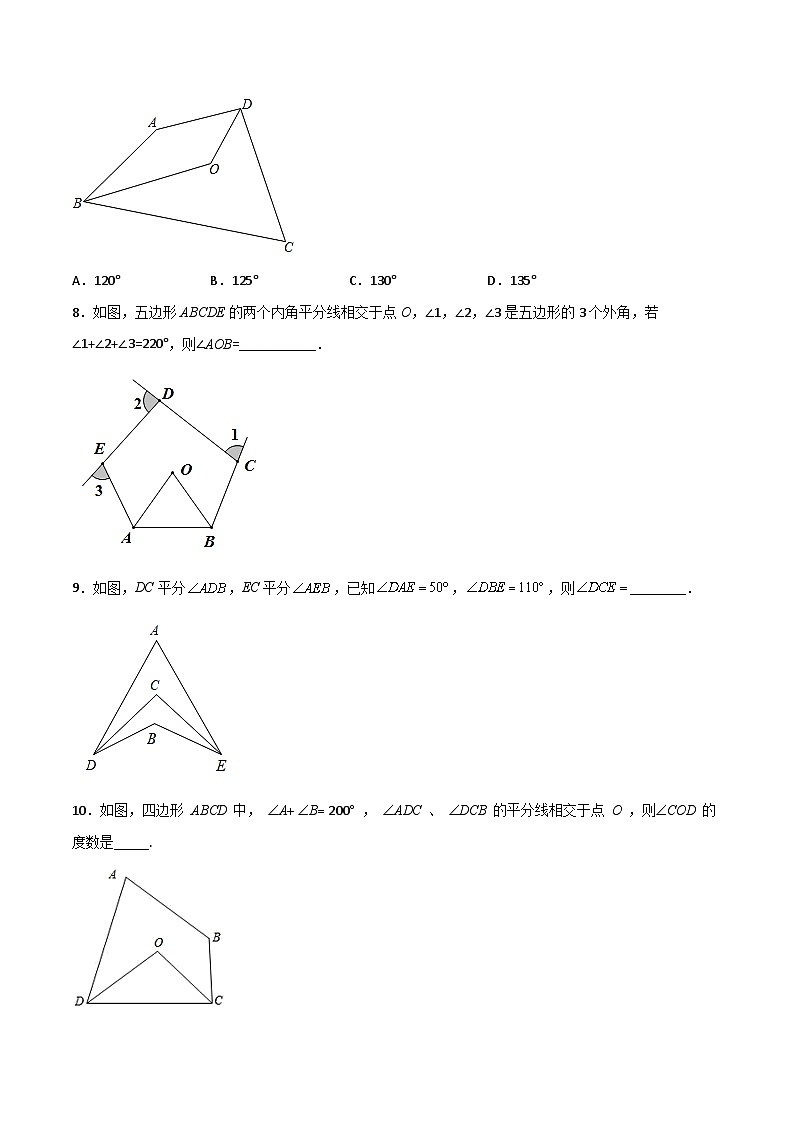
A．120° B．125° C．130° D．135°
【答案】D
【解析】
【分析】
由题意易得，由四边形内角和可知，则有，进而问题可求解．
【详解】
解：∵∠ABC与∠ADC的平分线交于点O，
∴，
∵∠A＝150°，∠C＝60°，
∴，
∴，
∴；
故选D．
【点睛】
本题主要考查四边形内角和及角平分线的定义，熟练掌握四边形内角和及角平分线的定义是解题的关键．
8．如图，五边形ABCDE的两个内角平分线相交于点O，∠1，∠2，∠3是五边形的3个外角，若∠1+∠2+∠3=220°，则∠AOB=___________．

【答案】70°
【解析】
【分析】
先求出与∠EAB和∠CBA相邻的外角的度数和，然后根据多边形外角和定理即可求解．
【详解】
如图，

∵∠1+∠2+∠3=220°，
∴∠4+∠5=360°-220°=140°，
∴∠EAB+∠CBA=220°，
∵AO，BO分别平分∠EAB，∠ABC，
∴∠OAB+∠OBA=110°，
∴∠AOB=180°-（∠OAB+∠OBA）=70°．
故答案是：70°．
【点睛】
本题主要考查了多边形外角和定理，三角形的内角和定理，熟练掌握多边形的外角和等于360°是解题的关键．
9．如图，DC平分，EC平分，已知，，则________．

【答案】
【解析】
【分析】
连接DE，根据三角形角平分线的性质及内角和定理可求出∠DCE与∠A、∠ADC、∠AEC之间的关系，同理可求出∠DCE与∠A、∠ADB、∠AEB之间的关系，代入数值进行计算即可；
【详解】
连接DE，如图1

在△BDE中，∠1＋∠2＝180°−∠DBE＝70°，
在△ADE中，∠ADE＋∠AED＝180°−∠DAE＝130°，
∴∠ADB＋∠AEB＝（∠ADE＋∠AED）−（∠1＋∠2）＝60°，
∵DC平分∠ADB，EC平分∠AEB，
∴∠3＋∠4＝30°，
在△DEC中，∠DCE＝180°−（∠1＋∠2）−（∠3＋∠4）
＝180°−70°−30°＝80°.
故答案为：.
【点睛】
本题考查三角形角平分线的性质及内角和定理，掌握上述知识点是解题关键.
10．如图，四边形 ABCD 中， ÐA+ ÐB= 200° ， ÐADC 、 ÐDCB 的平分线相交于点 O ，则ÐCOD 的度数是_____.

【答案】100
【解析】
【分析】
先根据四边形的内角和得到∠ADC+∠BCD=160°，再根据ÐADC 、 ÐDCB 的平分线得到∠ODC+∠OCD=80°，再根据三角形的内角和即可求解.
【详解】
∵四边形 ABCD 中， ÐA+ ÐB= 200°
∴∠ADC+∠BCD=360°-（ÐA+ ÐB）=160°
∵ÐADC 、 ÐDCB 的平分线相交于点 O
∴∠ODC+∠OCD=ÐADC+ÐDCB=（∠ADC+∠BCD）=80°，
在△COD中，ÐCOD=180°-（∠ODC+∠OCD）=100°.
故填：100.
【点睛】
此题主要考查四边形的角度求解，解题的关键是熟知多边形的内角和及角平分线的性质.
类型三 两内角平分线大题解答
11．探究与发现：
（1）探究一：三角形的一个内角与另两个内角的平分线所夹的角之间的关系？
已知：如图1，在中，DP、CP分别平分和，试探究与的数量关系，并说明理由．
（2）探究二：四边形的两个内角与另两个内角的平分线所夹的角之间的关系？
已知：如图2，在四边形ABCD中，DP、CP分别平分和，试探究与的数量关系，并说明理由．
（3）探究三：六边形的四个内角与另两个内角的平分线所夹的角之间的关系？
已知：如图3，在六边形ABCDEF中，DP、CP分别平分和，请求出与的数量关系．

【答案】（１）∠P=90°+∠A；（２）∠P =（∠A+∠B+∠E+∠F）-180°；（３）∠P=（∠A+∠B+∠E+∠F）-180°．
【解析】
【分析】
（1）先根据角平分线的定义表示出∠CDP和∠DCP，然后再根据三角形内角和为180°即可得到∠P和∠A的数量关系；
（2）先根据角平分线的定义表示出∠CDP和∠DCP，根据四边形内角和为360°，即可得到∠BCD+∠ADC=360°-（∠A+∠B），再结合三角形内角和为180°，可得∠P与∠A+∠B的数量关系；
（3）先根据角平分线的定义表示出∠CDP和∠DCP，根据六边形内角和为720"，可得∠BCD+∠ADC=720°-（∠A+∠B+∠E+∠F）,再结合三角形内角和为180°，可得∠P与∠A+∠B的数量关系．
【详解】
解：（1）∠P=90°+∠A,理由如下：
∵DP，CP分别平分∠ADC和∠ACD
∴∠CDP=∠ADC，∠DCP=∠ACD
∵∠A +∠ADC+∠ACD=180°
∴∠ADC+∠ACD=180°-∠A
∵∠P+∠PDC+∠PCD=180°
∴∠P=180°-（∠PDC+∠PCD）=180°-（∠ADC+∠ACD）
∴∠P=180°-（180°-∠A）=90°+∠A；
（2）∠P=（∠A+∠B）,理由如下：
∵DP，CP分别平分∠ADC和∠BCD
∴∠CDP=∠ADC，∠DCP=∠BCD
∵∠A +∠B+∠ADC+∠BCD=360°
∴∠BCD+ ∠ADC=360°-（∠A+∠B）
∵∠P+∠PDC+∠PCD=180°
∴∠P=180°-（∠PDC+∠PCD）
=180°-（∠ADC+∠BCD）
=180°-[360°-(∠A-∠B)]
= （∠A+∠B）；
（3）∠P=（∠A+∠B+∠E+∠F）-180°
理由如下：
∵DP，CP分别平分∠EDC和∠BCD
∴∠PDC=∠EDC，∠DCP=∠BCD
∵∠A+∠B+∠E+∠F+∠BCD+ ∠EDC=720°
∴∠BCD+∠EDC=720°-（∠A+∠B+∠E+∠F）
∵∠P+∠PDC+∠PCD=180°
∴∠P =180°-（∠PDC+∠PCD）
=180°-（∠EDC+∠BCD）
=180°-[720°-（∠A+∠B+∠E+∠F）]
=（∠A+∠B+∠E+∠F）-180°．
【点睛】
本题主要考查了多边形的内角和、角平分线的性质等知识点，掌握运用多边形的内角和表示角的数量关系是解答本题的关键．
12．如图①，ABC的角平分线BD、CE相交于点P．
（1）如果∠A＝80°，求∠BPC的度数；
（2）如图②，过P点作直线MN，分别交AB和AC于点M和N，且MN平行于BC，则有∠MPB+∠NPC＝90°﹣∠A．
①若将直线MN绕点P旋转，如图③，试探索∠MPB、∠NPC、∠A三者之间的数量关系是否依然成立，并说明理由；
②当直线MN与AB的交点仍在线段AB上，而与AC的交点在AC的延长线上时，如图④，试问①中∠MPB、∠NPC、∠A三者之间的数量关系是否仍然成立？若不成立，请给出∠MPB、∠NPC、∠A三者之间的数量关系，并说明你的理由．

【答案】（1）130°；（2）①仍然成立，见解析；②不成立，∠MPB﹣∠NPC＝90°﹣∠A，见解析
【解析】
【分析】
（1）运用三角形的内角和定理及角平分线的定义，首先求出∠1+∠2，进而求出∠BPC即可解决问题．
（2）运用（1）中的结论，结合三角形的内角和定理逐一分类解析，即可解决问题．
【详解】
解：（1）如图①∵在△ABC中，∠A+∠ABC+∠ACB＝180°，且∠A＝80°，
∴∠ABC+∠ACB＝100°，
∵∠1＝∠ABC，∠2＝∠ACB，
∴∠1+∠2＝（∠ABC+∠ACB）＝×100°＝50°，
∴∠BPC＝180°﹣（∠1+∠2）＝180°﹣50°＝130°．
（2）①如图③，由（1）知：∠BPC＝180°﹣（∠1+∠2）；
∵∠1+∠2＝（180°﹣∠A）＝90°-∠A，
∴∠BPC＝180°﹣（90°﹣∠A）＝90°+∠A；
∴∠MPB+∠NPC＝180°﹣∠BPC＝180°﹣（90°+∠A）＝90°﹣∠A．
②不成立，∠MPB﹣∠NPC＝90°﹣∠A．
如图④，由①知：∠BPC＝90°+∠A，
∴∠MPB﹣∠NPC＝180°﹣∠BPC
＝180°﹣（90°+∠A）
＝90°﹣∠A．


【点睛】
该题主要考查了三角形的内角和定理、角平分线的定义等几何知识点及其应用问题；牢固掌握三角形的内角和定理、角平分线的定义等几何知识点是基础，灵活运用是关键．
13．（1）特例发现：如图1，，平分，平分．请观察猜想的度数并说明理由；

（2）类比探究：如图2，点是上一点，当保持不变，移动直角顶点，使平分．与存在怎样的数量关系?并说明理由；
（3）拓展应用：如图3，为线段上一定点，点为直线上一动点，点不与点重合．与有何数量关系?猜想结论并说明理由．
【答案】（1），理由见解析；（2）．理由见解析；（3）或．（或）理由见解析．
【解析】
【分析】
（1）过点E作EF//AB，根据平行线的性质推出∠BAE=∠AEF，∠BAC+∠ACD=180°，根据角平分线的性质得出∠BAC=2∠EAC，∠ACD=2∠ACE，从而推出∠AEC=90°；
（2）过E作EF//AB，由平行线的性质推出∠BAE=∠AEF，∠FEC=∠DCE，结合图形有∠BAE+∠ECD=90°，再根据角平分线的性质推出∠MCE＝∠ECD=∠MCD，从而得到∠BAE+∠MCD＝90°；
（3）根据题意分当点Q在射线CD上运动时和当点Q在射线CD的反向延长线上运动时两种情况进行讨论，结合图形根据平行线的性质及三角形的内角和进行求解即可．
【详解】
解：（1）
理由如下：过点作，则．


，
.
平分，平分，
，，
，
，
即.
（2）．
过作，

，
，
，．
，
，
平分，，
.
（3）当点在射线上运动时（如图3），

（或）
理由：过点过作，
，
，
，．
.
当点在射线的反向延长线上运动时（点除外）

理由：，.
，

综上，或（或）
【点睛】
本题考查平行线的判定与性质，通常需要根据题意作出相关的辅助线（EF//AB），运用数形结合的思想方法，从图形中寻找角之间的位置关系根据平行线的性质从而判断角之间的大小关系，同时注意运用分类讨论的思想方法．
14．如图1，在平面直角坐标系中，A(，0)，C(b，2)，且满足，过C作CB⊥轴于B．


(1)求三角形ABC的面积．
(2)如图2，若过B作BD∥AC交轴于D，且AE，DE分别平分∠CAB，∠ODB，求∠AED的度数．
(3)若AC交轴于点F，在轴上是否存在点P，使得三角形ACP的面积是三角形AOF的面积的4倍？若存在，求出P点坐标；若不存在，请说明理由．
【答案】(1)4
(2)45°
(3)P坐标为(0，3)或(0，-1)
【解析】
【分析】
（1）根据非负数的性质可列出关于a、b的二元一次方程组，解出a、b，即得出A、B、C三点坐标，然后根据三角形面积公式计算即可；
（2）过E作EF∥AC，根据平行线的性质结合角平分线定义即可求解；
（3）连接OC．根据和，即可求出，从而可求出．分类讨论①当P点在x轴上方时，作轴，轴，轴，分别交于点M、N．设P(0，m)，根据，即可求出m的值，即得出答案；②当P点在x轴下方时，作轴，轴，轴，分别交于点、．设设P(0，n)，根据，即可求出n的值，即得出答案．
(1)
解：∵，
∴，
解得：．
∴A(-2，0)，C(2，2)．
∵CB⊥AB，
∴B(2，0)，
∴AB=4，CB=2，
∴；
(2)
如图，过E作EF∥AC．


∵CB⊥x轴，
∴CB∥y轴，∠CBA=90°，
∴∠ODB=∠6．
又∵BD∥AC，
∴∠CAB=∠5，
∴∠CAB+∠ODB=∠5+∠6=180°-∠CBA=90°．
∵BD∥AC，
∴BD∥AC∥EF，
∴∠1=∠3，∠2=∠4．
∵AE，DE分别平分∠CAB，∠ODB，
∴∠3=∠CAB，∠4=∠ODB，
∴∠AED=∠1+∠2=∠3+∠4=(∠CAB+∠ODB)=45°；
(3)
如图，连接OC．


∵，，
∴．
∵，，
∴．
∵，
∴．
分类讨论：①当P点在x轴上方时，如图，作轴，轴，轴，分别交于点M、N．
设P(0，m)


则AM=m，MP=2，NP=2，NC=m-2，MN=4，
∴


，
∴，
解得：．
∴此时点P坐标为(0，3)；
②当P点在x轴下方时，如图，作轴，轴，轴，分别交于点、．
设P(0，n)，


则=-n，=2，=2，=2-n，，
∴


，
∴，
解得：．
∴此时点P坐标为(0，-1)．
综上可知点P坐标为(0，3)或(0，-1)．
【点睛】
本题考查非负数的性质，解二元一次方程组，坐标与图形，角平分线的定义，三角形的面积公式，平行线的判定和性质．利用数形结合和分类讨论的思想是解题关键．