人教版八年级上册12.3 角的平分线的性质精品课后作业题

这是一份人教版八年级上册12.3 角的平分线的性质精品课后作业题，共10页。试卷主要包含了下列命题中真命题是等内容，欢迎下载使用。

一、选择题
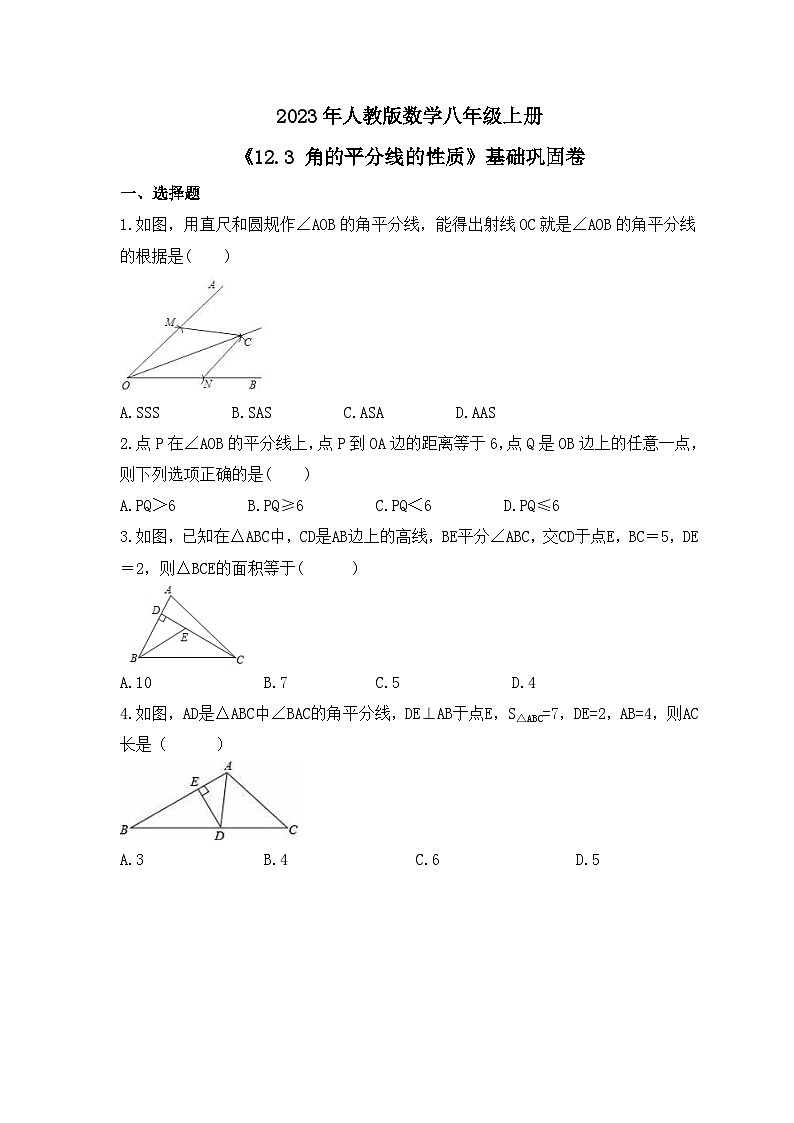
1.如图，用直尺和圆规作∠AOB的角平分线，能得出射线OC就是∠AOB的角平分线的根据是( )
A.SSS B.SAS C.ASA D.AAS
2.点P在∠AOB的平分线上，点P到OA边的距离等于6，点Q是OB边上的任意一点，则下列选项正确的是( )
A.PQ＞6 B.PQ≥6 C.PQ＜6 D.PQ≤6
3.如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC＝5，DE＝2，则△BCE的面积等于( )
A.10 B.7 C.5 D.4
4.如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S△ABC=7，DE=2，AB=4，则AC长是（ ）

A.3 B.4 C.6 D.5
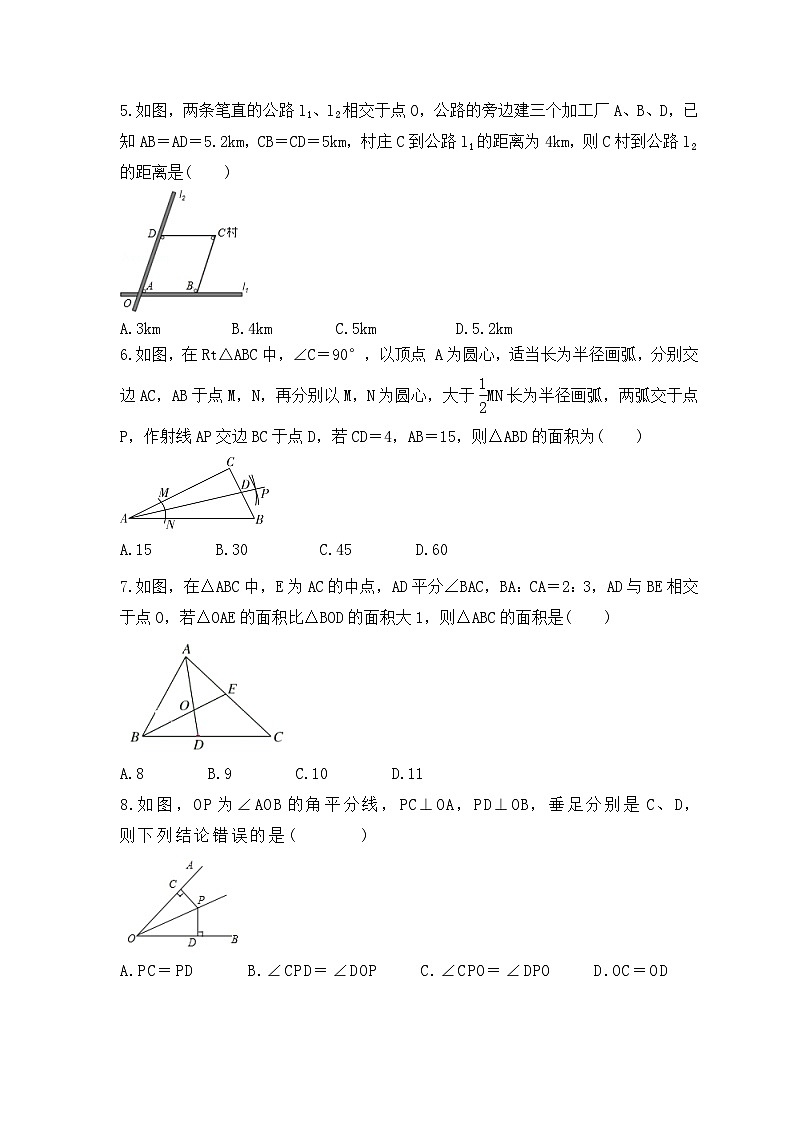
5.如图，两条笔直的公路l1、l2相交于点O，公路的旁边建三个加工厂A、B、D，已知AB＝AD＝5.2km，CB＝CD＝5km，村庄C到公路l1的距离为4km，则C村到公路l2的距离是( )
A.3km B.4km C.5km
6.如图，在Rt△ABC中，∠C＝90°，以顶点 A为圆心，适当长为半径画弧，分别交边AC，AB于点M，N，再分别以M，N为圆心，大于eq \f(1,2)MN长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD＝4，AB＝15，则△ABD的面积为( )
A.15 B.30 C.45 D.60
7.如图，在△ABC中，E为AC的中点，AD平分∠BAC，BA：CA＝2：3，AD与BE相交于点O，若△OAE的面积比△BOD的面积大1，则△ABC的面积是( )
A.8 B.9 C.10 D.11
8.如图，OP为∠AOB的角平分线，PC⊥OA，PD⊥OB，垂足分别是C、D，则下列结论错误的是( )
A.PC＝PD B.∠CPD＝∠DOP C.∠CPO＝∠DPO D.OC＝OD
9.如图，∠B＝∠C＝90°，M是BC的中点，DM平分∠ADC，且∠ADC＝110°，则∠MAB＝( )
A.30° B.35° C.45° D.60°
10.下列命题中真命题是( )
A.三角形按边可分为不等边三角形，等腰三角形和等边三角形
B.等腰三角形任一个内角都有可能是钝角或直角
C.三角形的一个外角大于任何一个内角
D.三角形三条内角平分线相交于一点，这点到三角形三边的距离相等
11.如图，OP平分∠AOB，PC⊥OA于C，点D是OB上的动点，若PC＝6cm，则PD的长可以是( )
A.3cm B.4cm C.5cm D.7 cm
12.数学课上，小明进行了如下的尺规作图（如图所示）：
（1）在△AOB（OA＜OB）边OA、OB上分别截取OD、OE，使得OD=OE；
（2）分别以点D、E为圆心，以大于0.5DE为半径作弧，两弧交于△AOB内的一点C；
（3）作射线OC交AB边于点P.
那么小明所求作的线段OP是△AOB的（ ）
A.一条中线 B.一条高 C.一条角平分线 D.不确定
二、填空题
13.到三角形三条边的距离都相等的点是这个三角形的 的交点.
14.如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直.若AD＝8，则点P到BC的距离是
15.如图所示，BD是∠ABC的平分线，DE⊥AB于点E，AB＝36cm，BC＝24cm，S△ABC＝144cm，则DE的长是 .
16.如图，O是△ABC内一点，且O到三边AB、BC、CA的距离OF＝OD＝OE，若∠BAC＝70°，∠BOC＝ .
17.如图，AD是△ABC的角平分线，若AB=2AC，则S△ABD∶S△ACD= ．
18.如图，O是直线BC上的点，OM平分∠AOB，ON平分∠AOC，点E在OM上，过点E作EG⊥OA于点G，EP⊥OB于点P，延长EG，交ON于点F，过点F作FQ⊥OC于点Q，若EF＝10，则FQ＋EP的长度为 .
三、解答题
19.如图，在Rt△ABC中，∠ABC=60°，BC=eq \r(3)．

①在BC、BA上分别截取BD、BE，使BD=BE；
②分别以D、E为圆心、以大于0.5DE的长为半径作圆弧，在∠ABC内两弧交于点O；
③作射线BO交AC于点F．
若点P是AB上的动点，则FP的最小值为 ．
20.如图，已知：CD⊥AB于D，BE⊥AC于E，且BD＝CE，BE交CD于点O.
求证：AO平分∠BAC.
21.我们把两组邻边相等的四边形叫做“筝形”.如图，四边形ABCD是一个筝形，其中AB＝CB，AD＝CD.对角线AC，BD相交于点O，OE⊥AB，OF⊥CB，垂足分别是E，F.求证OE＝OF.
22.如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，△ABC的面积是28cm2，AB=16cm，AC=12cm，求DE的长.
23.如图，Rt△ABC中，∠ACB＝90°.
(1)作∠BAC的角平分线交BC于点D(要求：用尺规作图，不写作法，保留作图痕迹)；
(2)在(1)的条件下，若AB＝10cm，△ADB的面积为15cm2，求CD的长.
24.已知：△ABC内部一点O到两边AB、AC所在直线的距离相等，且OB＝OC.
求证：AB＝AC.
25.如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC＝CD.
(1)求证：△BCE≌△DCF；
(2)求证：AB＋AD＝2AE.
答案
1.A.
2.B.
3.C
4.A
5.B
6.B.
7.C.
8.B
9.B.
10.D.
11.D.
12.C.
13.答案为：内角平分线
14.答案为：4.
15.答案为：4.8cm.
16.答案为：125°.
17.答案为：2
18.答案为：10.
19.答案为：1．
20.证明：∵OD⊥AB，OE⊥AC
∴∠BDO＝∠CEO＝90°，
又∵∠BOD＝∠COE，BD＝CE，
∴△BOD≌△COE
∴OD＝OE
又由已知条件得△AOD和△AOE都是Rt△，且OD＝OE，OA＝OA，
∴Rt△AOD≌Rt△AOE.
∴∠DAO＝∠EAO，
即AO平分∠BAC.
21.证明：∵在△ABD和△CBD中，
，
∴△ABD≌△CBD(SSS)，
∴∠ABD＝∠CBD，
∴BD平分∠ABC.
又∵OE⊥AB，OF⊥CB，
∴OE＝OF.
22.解： 利用角平分线的性质，得出DE=DF，再利用△ABC面积是28cm2可求DE.
∵AD为∠BAC的平分线，DE⊥AB，DF⊥AC，
∴DE=DF，
∵S△ABC=S△ABD＋S△ACD=eq \f(1,2)AB×DE＋eq \f(1,2)AC×DF
∴S△ABC=eq \f(1,2)（AB＋AC）×DE
即eq \f(1,2)×（16＋12）×DE=28，
故DE=2（cm）.
23.解：(1)如图所示，AD即为所求；
(2)过D作DE⊥AB，E为垂足，
由△ADB的面积为15cm2，
得eq \f(1,2)AB•ED＝15，解得：ED＝3cm，
∵AD平分∠BAC，DE⊥AB，∠ACB＝90°
∴CD＝ED＝3cm.
24.证明：在Rt△BOF和Rt△COE中，
，
∴Rt△BOF≌Rt△COE，
∴∠FBO＝∠ECO，
∵OB＝OC，
∴∠CBO＝∠BCO，
∴∠ABC＝∠ACB，
∴AB＝AC.
25.证明：(1)∵AC是角平分线，CE⊥AB于E，CF⊥AD于F，
∴CE＝CF，∠F＝∠CEB＝90°，
在Rt△BCE和Rt△DCF中，
∴△BCE≌△DCF；
(2)解：∵CE⊥AB于E，CF⊥AD于F，
∴∠F＝∠CEA＝90°，
在Rt△FAC和Rt△EAC中，
，
∴Rt△FAC≌Rt△EAC，
∴AF＝AE，
∵△BCE≌△DCF，
∴BE＝DF，
∴AB＋AD＝(AE＋BE)＋(AF﹣DF)＝AE＋BE＋AE﹣DF＝2AE.