



- 第十二章 全等三角形 重难点检测卷-2023-2024学年八年级数学上册重难点专题提升精讲精练(人教版) 试卷 0 次下载
- 专题08 等腰三角形、直角三角形中的分类讨论问题专训-2023-2024学年八年级数学上册重难点专题提升精讲精练(人教版) 试卷 1 次下载
- 专题10 轴对称中的翻折、旋转问题专训-2023-2024学年八年级数学上册重难点专题提升精讲精练(人教版) 试卷 2 次下载
- 专题11 轴对称图形的经典压轴题型专训-2023-2024学年八年级数学上册重难点专题提升精讲精练(人教版) 试卷 3 次下载
- 第十三章 轴对称 重难点检测卷-2023-2024学年八年级数学上册重难点专题提升精讲精练(人教版) 试卷 0 次下载
初中数学人教版八年级上册13.1.1 轴对称精品巩固练习
展开题型一求两条线段和的最小值
题型二求两条线段差的最大值
题型三求三条线段和的最小值(双动点问题)
题型四最值问题的实际应用
【知识梳理】
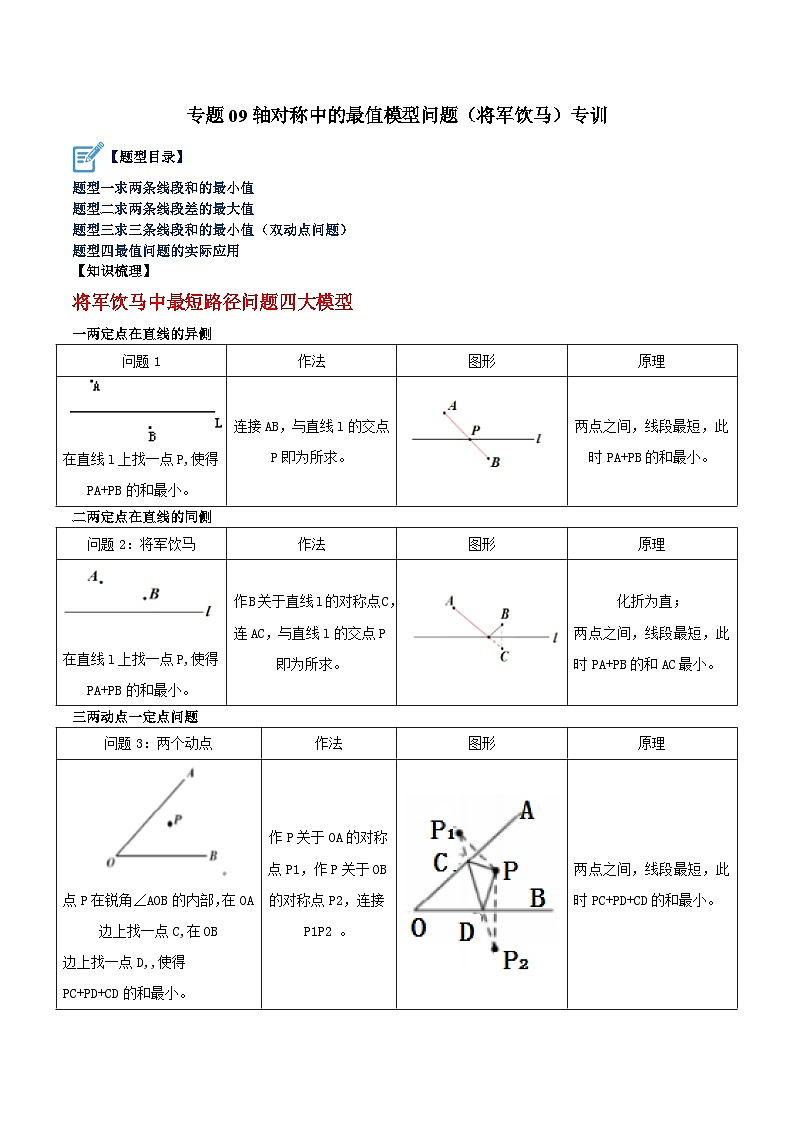
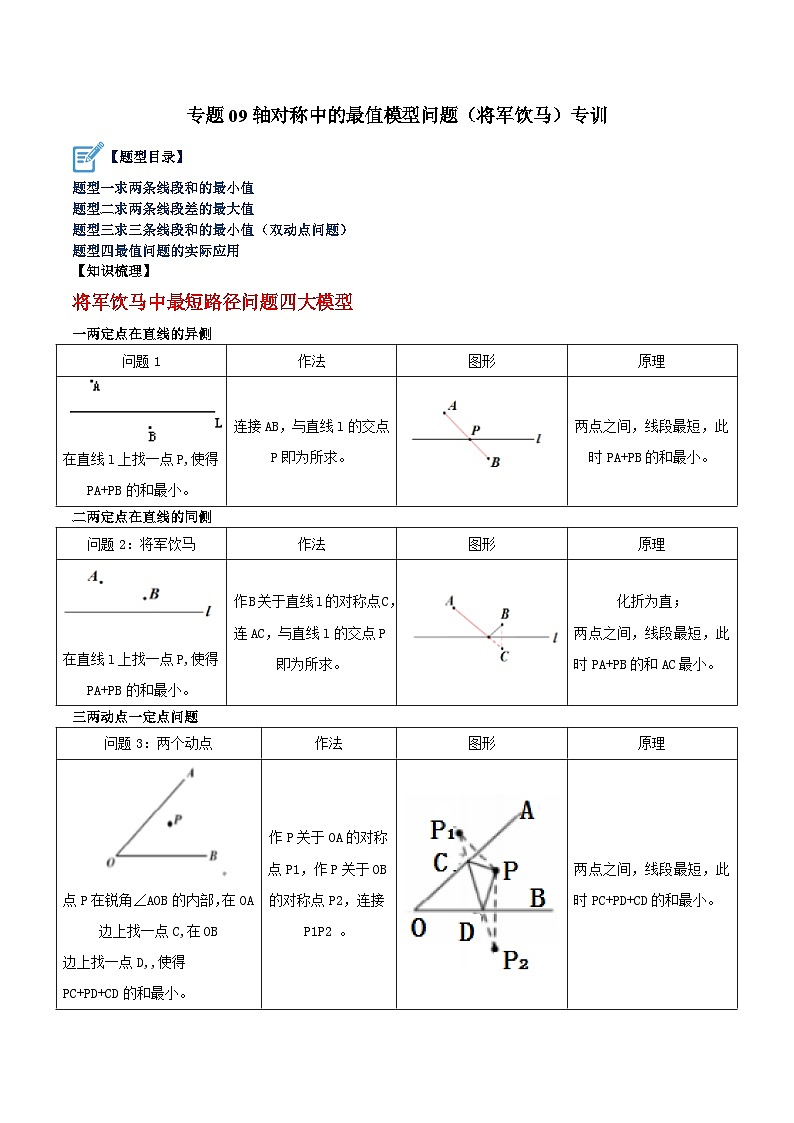
将军饮马中最短路径问题四大模型
一两定点在直线的异侧
二两定点在直线的同侧
三两动点一定点问题
四造桥选址问题
注意:本专题部分题目涉及勾股定理,各位同学可以先行学习第3章后再完成该专题训练.
勾股定理公式:a2+b2=c2
【经典例题一求两条线段和的最小值】
【例1】(2022秋·黑龙江齐齐哈尔·八年级校考阶段练习)如图,在ABC中,,,,是中点,垂直平分,交于点,交于点,在上确定一点,使最小,则这个最小值为( )
A.10B.11C.12D.13
【变式训练】
1.(2023·江苏·八年级假期作业)如图,中,,,,于点D,1.(2023春·河南郑州·七年级统考期末)如图,在中,AB=AC=7,AD=8.3,点E在AD上,CE=CB,CF平分∠BCE交AD于点F.点P是线段CF上一动点,则EP+AP的最小值为( )
A.6B.7C.7.5D.8.3
2.(2023秋·八年级课时练习)如图,在中,,,是的两条中线,是线段上的一个动点,则下列线段的长等于最小值的是( )
A.B.C.D.
3.(2023春·广东揭阳·七年级惠来县第一中学校考期末)如图,在等腰中,,,作于点D,,点E为边上的中点,点P为上一动点,则的最小值为.
4.(2023·广西防城港·统考三模)如图,在中,,,,点O是的中点,点D是线段上任意一点(不含端点),连接,则的最小值为.
5.(2023春·全国·七年级专题练习)如图,等边(三边相等,三个内角都是的三角形)的边长为,动点D和动点E同时出发,分别以每秒的速度由A向B和由C向A运动,其中一个动点到终点时,另一个也停止运动,设运动时间为t,,和交于点F.
(1)在运动过程中,与始终相等吗?请说明理由;
(2)连接,求t为何值时,;
(3)若于点M,点P为上的点,且使最短.当时,的最小值为多少?请直接写出这个最小值,无需说明理由.
6.(2022秋·广东广州·八年级校考期末)如图,在中,.
(1)作的垂直平分线交于点,交于点(保留作图痕迹).
(2)连接,若,的周长是.
①求的长;
②在直线上是否存在点,使的值最小,若存在,标出点的位置并求的最小值,若不存在,说明理由.
【经典例题二求两条线段差的最大值】
【例2】如图,点,在直线的同侧,到的距离,到的距离,已知,是直线上的一个动点,记的最小值为,的最大值为,则的值为( )
A.160B.150C.140D.130
【变式训练】
1.如图,在等边中,E是边的中点,P是的中线上的动点,且,则的最大值是________.
【经典例题三求三条线段和的最小值(双动点问题)】
【例3】(2021秋·重庆荣昌·八年级校考阶段练习)如图,∠AOB=30º,∠AOB 内有一定点P,且OP=12,在OA 上有一动点Q,OB 上有一动点R.若△PQR 周长最小,则最小周长是( )
A.6B.12C.16D.20
【变式训练】
1.(2022秋·湖北黄石·八年级统考期中)如图,中,,,的面积为21,于D,EF是AB边的中垂线,点P是EF上一动点,周长的最小是等于( )
A.7B.8C.9D.10
2.(2021秋·浙江·八年级期中)如图,,内有一定点P,且.在上有一动点Q,上有一动点R.若周长最小,则最小周长是________.
3.(2020秋·江苏苏州·八年级校考阶段练习)最短路径问题:
例:如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短.
解:只有A、C、B在一直线上时,才能使AC+BC最小.作点A关于直线“街道”的对称点A′,然后连接A′B,交“街道”于点C,则点C就是所求的点.
应用:已知:如图A是锐角∠MON内部任意一点,
在∠MON的两边OM,ON上各取一点B,C,组成三角形,使三角形周长最小.
(1)借助直角三角板在下图中找出符合条件的点B和C.
(2)若∠MON=30°,OA=10,求三角形的最小周长.
【经典例题四最值问题的实际应用】
【例4】(2023春·四川成都·七年级统考期末)如图,在正方形网格中,每个小正方形的边长都是一个单位长度,的三个顶点都在格点上.
(1)求出的面积;
(2)画出关于直线对称的;
(3)在直线上画出点,使得的值最小.
【变式训练】
1.(2023·浙江·八年级假期作业)如图,已知,两点在直线的同一侧,根据题意,用尺规作图.
(1)在(图①)直线上找出一点,使;
(2)在(图②)直线上找出一点,使的值最小;
(3)在(图③)直线上找出一点,使的值最大.
2.(2023春·全国·八年级专题练习)如图,在中,已知,的垂直平分线交于点N,交于点M,连接.
(1)若,则的度数是___________度;
(2)若.的周长是,
①求的长度;
②若点P为直线上一点,请你直接写出周长的最小值.
3.(2023秋·重庆沙坪坝·七年级重庆八中校考期末)如图,已知点A,B,C,D是不在同一直线上的四个点,请按要求画出图形.
(1)作线段和射线;
(2)用无刻度的直尺和圆规在射线上作;
(3)在平面内作一点P,使得的和最短.
【重难点训练】
1.(2023春·辽宁阜新·七年级校考阶段练习)如图,等腰三角形的底边长为4,面积是16,腰的垂直平分线分别交,边于E,F点,若点D为边的中点,点M为线段上一动点,则周长的最小值为( )
A.12B.8C.10D.20
2.(2022秋·河南驻马店·八年级统考期中)如图,边长为的等边中,是上中线且,点在上,连接,在的右侧作等边,连接,则周长的最小值是( )
A.B.C.D.
3.(2023·安徽合肥·统考一模)如图,在中,,,是下方的一动点,记,的面积分别记为,.若,则线段长的最小值是( )
A.3B.C.D.
4.(2023春·全国·七年级专题练习)如图,,,分别是边,上的定点,,分别是边,上的动点,记,,当最小时,则关于,的数量关系正确的是( )
A.B.C.D.
5.(2022秋·江苏无锡·八年级校考阶段练习)如图.在五边形ABCDE中,∠AMN+∠ANM=,∠B=∠E=,在BC、DE上分别找一点M、N,使得的周长最小时,则∠BAE的度数为( )
A.136°B.96°C.90°D.84°
6.(2023春·广东广州·八年级广州市真光中学校考开学考试)如图,在锐角三角形ABC中,BC=4,∠ABC=60°,BD平分∠ABC,交AC于点D,M、N分别是BD,BC上的动点,则CM+MN的最小值是( )
A.B.2C.D.4
7.(2020秋·广东广州·八年级校考期中)如图所示,∠AOB=60°,点P是∠AOB内一定点,并且OP=2,点M、N分别是射线OA,OB上异于点O的动点,当△PMN的周长取最小值时,点O到线段MN的距离为( )
A.1B.2C.4D.1.5
8.(2023秋·河南驻马店·八年级统考期末)如图,在中,,以AC为底边在外作等腰,过点D作的平分线分别交AB,AC于点E,F.若,,点P是直线DE上的一个动点,则周长的最小值为( )
A.15B.17C.18D.20
9.(2023春·全国·八年级专题练习)在中,,D是边上一点,,E,F分别是边上的动点,则的最小值为.
10.(2023春·重庆南岸·八年级重庆市广益中学校校考阶段练习)如图,等腰三角形的底边长为2,面积是6,腰的垂直平分线分别交,于点E、F,若点D为底边的中点,点M为线段上一动点,则的周长的最小值为.
11.(2023春·江苏无锡·九年级统考期中)如图,在中,,点是边上的一动点.已知,现将绕点按逆时针方向旋转,点是边的中点,则,长度的最小值为.
12.(2023春·八年级课时练习)如图,,,分别为射线,上的动点,为内一点,连接,,.若,则周长的最小值为.
13.(2022秋·全国·八年级期末)如图,在△ABC中,∠CAB=30°,∠ACB=90°,AC=3,D为AB的中点,E为线段AC上任意一点(不与端点重合),当E点在线段AC上运动时,则DE+CE的最小值为.
14(2022秋·广东惠州·八年级校考阶段练习)如图,,点,分别在射线,上,且,,点,分别是射线,上的动点,求的最小值为.
15.(2022秋·八年级课时练习)如图,是的角平分线,,垂足为.若,,则的度数为.
16.(2022秋·全国·八年级专题练习)如图,在中,,,是的两条中线,是上的一个动点,则图中长度与的最小值相等的线段是.
17.(2023·浙江·八年级假期作业)如图,已知,两点在直线的同一侧,根据题意,用尺规作图.
(1)在(图①)直线上找出一点,使;
(2)在(图②)直线上找出一点,使的值最小;
(3)在(图③)直线上找出一点,使的值最大.
18(2022秋·北京昌平·七年级统考期末)如图,在正方形网格中画有一段笔直的铁路及道口A,B和村庄M,N.完成以下作图.
(1)若在村庄N与道口A之间修一条最短的公路,在图中画出此公路,并说明这样画的理由;
(2)若在公路上选择一个地点P安装实时监控系统,要求点P到村庄N与道口B的距离相等,在图中标出点P的位置;
(3)当一节火车头行驶至铁路上的点Q时,距离村庄N最近.在图中确定点Q的位置(保留作图痕迹);
(4)若在道口A或B处修建一座火车站,使得到两村的距离和较短,应该修在________处.
19.(2023秋·重庆沙坪坝·七年级重庆八中校考期末)如图,已知点A,B,C,D是不在同一直线上的四个点,请按要求画出图形.
(1)作线段和射线;
(2)用无刻度的直尺和圆规在射线上作;
(3)在平面内作一点P,使得的和最短.
20.(2022秋·湖北宜昌·八年级校考期中)已知,村庄和村庄都位于笔直的小河l同侧,要在河边建一引水站,使它到村庄,需铺设的水管长度之和最小.
(1)请画出引水站的位置,并连接(包括画图痕迹);
(2)若不计杂料,所用水管之和为米,且比长米,两村庄购买水管花费元,约定按长度分摊费用,请计算两村庄各需付水管购买费多少元?
21.(2023春·全国·七年级专题练习)(1)唐朝诗人李顾的诗古从军行开头两句:“白日登山望烽火,黄昏饮马傍交河”,诗中隐含着一个有趣的数学问题:如图所示,诗中大意是将军从山脚下的点出发,带着马走到河边点饮水后,再回到点宿营,请问将军怎样走才能使总路程最短?请你通过画图,在图中找出点,使的值最小,不说明理由;
(2)实践应用,如图,点为内一点,请在射线、上分别找到两点、,使的周长最小,不说明理由;
(3)实践应用:如图,在中,,,,,平分,、分别是、边上的动点,求的最小值.
22.(2023秋·吉林松原·八年级统考期末)如图,在中,,,,平分,交边于点,点是边的中点.点为边上的一个动点.
(1)______,______度;
(2)当四边形为轴对称图形时,求的长;
(3)若是等腰三角形,求的度数;
(4)若点在线段上,连接、,直接写出的值最小时的长度.
问题1
作法
图形
原理
在直线l上找一点P,使得
PA+PB的和最小。
连接AB,与直线l的交点P即为所求。
两点之间,线段最短,此时PA+PB的和最小。
问题2:将军饮马
作法
图形
原理
在直线l上找一点P,使得
PA+PB的和最小。
作B关于直线l的对称点C,连AC,与直线l的交点P即为所求。
化折为直;
两点之间,线段最短,此时PA+PB的和AC最小。
问题3:两个动点
作法
图形
原理
点P在锐角∠AOB的内部,在OA边上找一点C,在OB
边上找一点D,,使得
PC+PD+CD的和最小。
作P关于OA的对称点P1,作P关于OB的对称点P2,连接P1P2 。
两点之间,线段最短,此时PC+PD+CD的和最小。
问题4:造桥选址
作法
图形
原理
直线m∥n,在m,n上分别求点M、N,使MN⊥m,MN⊥n,且AM+MN+BN的和最小。
将点A乡向下平移MN的长度得A1,连A1B,交n于点N,过N作NM⊥m于M。
两点之间,线段最短,此时AM+MN+BN的最小值为A1B+MN。
专题64 将军饮马模型与最值问题-中考数学重难点专项突破(全国通用): 这是一份专题64 将军饮马模型与最值问题-中考数学重难点专项突破(全国通用),文件包含专题64将军饮马模型与最值问题原卷版docx、专题64将军饮马模型与最值问题解析版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
最新中考数学难点突破与经典模型精讲练 专题17 最值问题中的将军饮马模型 (全国通用): 这是一份最新中考数学难点突破与经典模型精讲练 专题17 最值问题中的将军饮马模型 (全国通用),文件包含专题17最值问题中的将军饮马模型原卷版docx、专题17最值问题中的将军饮马模型解析版docx等2份试卷配套教学资源,其中试卷共56页, 欢迎下载使用。
专题03 绝对值中的最值与化简压轴问题专训-2023-2024学年七年级数学上册重难点专题提升精讲精练(人教版): 这是一份专题03 绝对值中的最值与化简压轴问题专训-2023-2024学年七年级数学上册重难点专题提升精讲精练(人教版),文件包含专题03绝对值中的最值与化简压轴问题专训原卷版docx、专题03绝对值中的最值与化简压轴问题专训解析版docx等2份试卷配套教学资源,其中试卷共97页, 欢迎下载使用。