高中数学人教A版 (2019)必修第一册4.2 指数函数课前预习课件ppt

展开

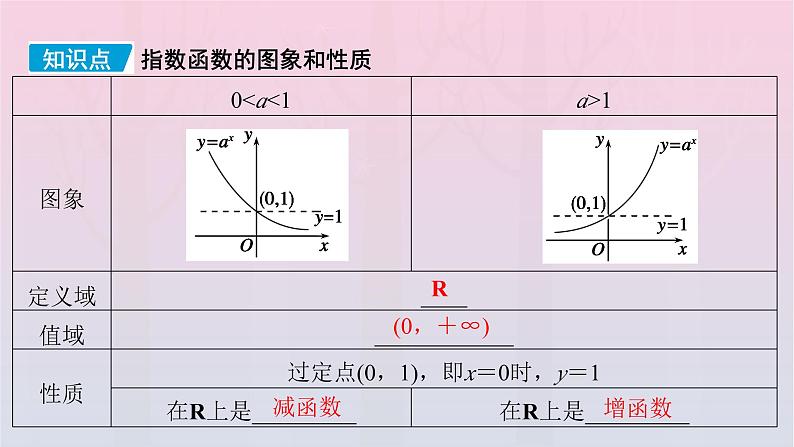
这是一份高中数学人教A版 (2019)必修第一册4.2 指数函数课前预习课件ppt，共36页。PPT课件主要包含了2指数函数，必备知识·探新知，0＋∞，减函数，增函数，关键能力·攻重难，课堂检测·固双基等内容，欢迎下载使用。

4.2.2　指数函数的图象和性质
第1课时　指数函数的图象和性质(一)
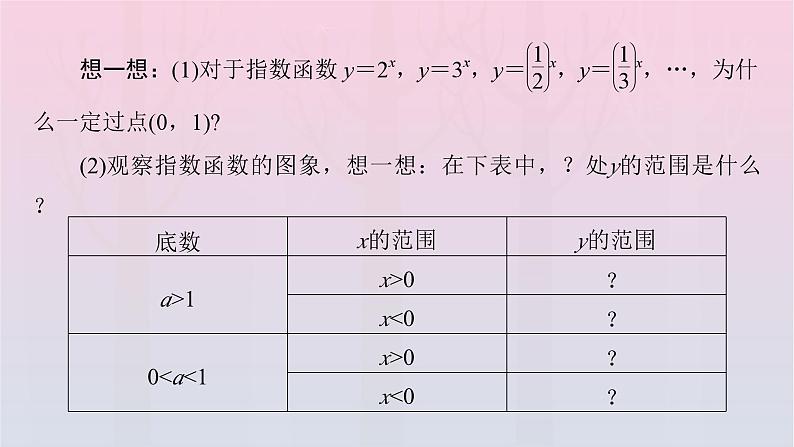
(2)观察指数函数的图象，想一想：在下表中，？处y的范围是什么？
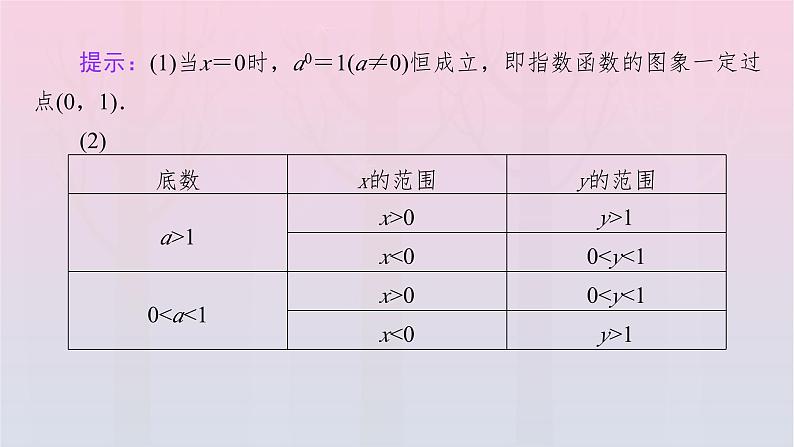
提示：(1)当x＝0时，a0＝1(a≠0)恒成立，即指数函数的图象一定过点(0，1)．(2)
练一练：1．下列说法正确的个数是(　　)(1)指数函数的图象都在x轴的上方．(2)若指数函数y＝ax是减函数，则02x.A．0　　　　B．1C．2　　D．3[解析]　对于(1)，由指数函数的性质可知正确．对于(2)，由指数函数的单调性可知正确．对于(3)，由y＝3x，y＝2x的图象可知，当x<0时，3x<2x，故(3)不正确．
A．增函数　　B．奇函数C．偶函数　　D．减函数
3．函数y＝1－2x，x∈[0，1]的值域是(　　)A．[0，1]B．[－1，0][解析]　∵0≤x≤1，∴1≤2x≤2，∴－1≤1－2x≤0，选B．
如图所示是下列指数函数的图象：(1)y＝ax；(2)y＝bx；(3)y＝cx；(4)y＝dx.则a，b，c，d与1的大小关系是(　　)A．a[分析]　根据指数函数的底数与图象间的关系来进行判断．[解析]　可先分为两类，(3)(4)的底数一定大于1，(1)(2)的底数一定小于1，然后再由(3)(4)比较，c，d的大小，由(1)(2)比较a，b的大小．当指数函数的底数大于1时，图象上升，且当底数越大，图象向上越靠近y轴；当底数大于0小于1时，图象下降，且当底数越小，图象向下越靠近x轴，故选B．[归纳提升]　指数函数图象的变化规律指数函数的图象随底数变化的规律可归纳为：在第一象限内，图象自下而上对应的底数依次增大．
[解析]　按规律，C1，C2，C3，C4的底数a依次增大，故选D．
(2)若函数y＝ax＋(b－1)(a>0，且a≠1)的图象不经过第二象限，则有(　　)A．a>1且b<1　　B．00　　D．a>1且b≤0[解析]　由函数图象不过第二象限知a>1，且x＝0时，a0＋(b－1)≤0，∴b≤0，故选D．
求下列函数的定义域和值域：[分析]　定义域是使函数解析式有意义的自变量的取值集合，值域是函数值的集合，依据定义域和函数的单调性求解．
[归纳提升]　1.函数单调性在求函数值域中的应用(1)若函数f(x)在区间[a，b]上是增函数，则f(a)≤f(x)≤f(b)，值域为[f(a)，f(b)]．(2)若函数f(x)在区间[a，b]上是减函数，则f(a)≥f(x)≥f(b)，值域为[f(b)，f(a)]．
2．函数y＝af(x)定义域、值域的求法(1)定义域．函数y＝af(x)的定义域与y＝f(x)的定义域相同．(2)值域．①换元，令t＝f(x)；②求t＝f(x)的定义域x∈D；③求t＝f(x)的值域t∈M；④利用y＝at的单调性求y＝at，t∈M的值域．
比较下列各题中两个值的大小．(1)1.82.2，1.83；　　　　(2)0.7－0.3，0.7－0.4；
[解析]　(1)∵1.82.2，1.83可看作函数y＝1.8x的两个函数值，∵1.8>1，∴y＝1.8x在R上为增函数，又2.2<3，∴1.82.2<1.83.(2)∵y＝0.7x在R上为减函数，又∵－0.3>－0.4，∴0.7－0.3<0.7－0.4.(3)∵1.90.4>1.90＝1，0.92.4<0.90＝1，∴1.90.4>
[归纳提升]　1．比较幂值大小的三种类型及处理方法
2．解指数不等式的类型及应注意的问题(1)形如ax>ab的不等式，借助于函数y＝ax的单调性求解，如果a的取值不确定，要对a分为01两种情况分类讨论．(2)形如ax>b的不等式，注意将b转化为以a为底数的指数幂的形式，再借助于函数y＝ax的单调性求解．3．函数y＝af(x)(a>0，a≠1)的单调性的处理技巧当a>1时，y＝af(x)与y＝f(x)的单调性相同，当0【对点练习】❸ 比较下列每组中两个数的大小：(1)1.72.5，1.73；(2)0.8－0.1，0.8－0.2；(4)1.70.3，[解析]　(1)考查指数函数y＝1.7x，由于底数1.7>1，∴指数函数y＝1.7x在(－∞，＋∞)上是增函数．∵2.5<3，∴1.72.5<1.73.
(2)考查函数y＝0.8x，由于0<0.8<1，∴指数函数y＝0.8x在(－∞，＋∞)上为减函数．∵－0.1>－0.2，∴0.8－0.1<0.8－0.2.(4)由指数函数的性质得1.70.3>1.70＝1，0.93.1<0.90＝1，∴1.70.3>
A．原点对称　　B．x轴对称C．y轴对称　　D．直线y＝－x对称
2．若函数f(x)＝(2a－1)x是R上的减函数，则实数a的取值范围是(　　)A．(0，1)　　B．(1，＋∞)
3．(2021·安徽合肥众兴中学高一期末测试)函数y＝ax－2＋1(a>0且a≠1)的图象必经过点(　　)A．(0，1)　　B．(1，1)C．(2，0)　　D．(2，2)[解析]　令x－2＝0，即x＝2，y＝a0＋1＝2，故选D．

相关课件更多