高中数学人教A版 (2019)必修 第一册4.2 指数函数精品习题
展开专题4.2 对数与对数函数
1.对数的性质
根据对数的概念,知对数具有以下性质:
(1)负数和零没有对数,即;
(2)1的对数等于0,即;
(3)底数的对数等于1,即;
(4)对数恒等式.
2.对数的运算性质
如果,那么:
(1);
(2);
(3).
3.对数的换底公式
对数的换底公式:.
换底公式的变形及推广:
(1);
(2);
(3)(其中a,b,c均大于0且不等于1,d>0).
4.对数运算的一般思路
(1)对于指数式、对数式混合型条件的化简与求值问题,一般可利用指数与对数的关系,将所给条件统一为对数式或指数式,再根据有关运算性质求解;
(2)在对数运算中,可先利用幂的运算性质把底数或真数变形,化成分数指数幂的形式,使幂的底数最简,然后运用对数的运算性质、换底公式,将对数式化为同底数对数的和、差、倍数运算.
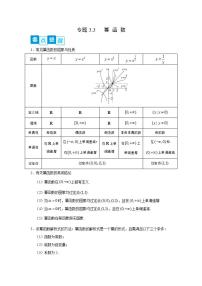
5.对数函数的图象和性质
一般地,对数函数的图象与性质如下表所示:
| ||
图象 | ||
定义域 | ||
值域 | ||
性质 | 过定点,即时, | |
在上是减函数 | 在上是增函数 | |
当x>1时,y<0; 当0<x<1时,y>0 | 当x>1时,y>0; 当0<x<1时,y<0 | |
在直线的右侧,当时,底数越大,图象越靠近x轴;当时,底数越小,图象越靠近x轴,即“底大图低”.
6.对数函数的图象过定点(1,0),所以讨论与对数函数有关的函数的图象过定点的问题,只需令真数为1,解出相应的,即可得到定点的坐标.
7.当底数时,对数函数是上的增函数,当时,底数的值越小,函数图象越“陡”,其函数值增长得越快;当底数时,对数函数是上的减函数,当时,底数的值越大,函数图象越“陡”,其函数值减小得越快.也可作直线y=1与所给图象相交,交点的横坐标即为各个底数,依据在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大,可比较底数的大小.
8.对一些可通过平移、对称变换作出其图象的对数型函数,在求解其单调性(单调区间)、值域(最值)、零点时,常利用数形结合思想求解.特别地,要注意底数和的两种不同情况.有些复杂的问题,借助于函数图象来解决,就变得简单了,这是数形结合思想的重要体现.
9.一些对数型方程、不等式问题常转化为相应的函数图象问题,利用数形结合法求解.
10.求对数型函数定义域的策略
列出对应的不等式(组)求解,注意对数函数的底数和真数的取值范围.
11.比较对数式的大小:
(1)若底数为同一常数,则可由对数函数的单调性直接进行判断;若底数为同一字母,则需对底数进行分类讨论;
(2)若底数不同,真数相同,则可以先用换底公式化为同底后,再进行比较;
(3)若底数与真数都不同,则常借助1,0等中间量进行比较.
12.解对数不等式:
(1)形如的不等式,借助的单调性求解,如果a的取值不确定,需分与两种情况讨论;
(2)形如的不等式,需先将b化为以a为底的对数式的形式,再借助的单调性求解.
一、单选题
1.某种水果失去的新鲜度与其采摘后时间(小时)近似满足函数关系式为(为非零常数).若采摘后20小时,这种水果失去的新鲜度为20%,采摘后30小时,这种水果失去的新鲜度为40%.那么采摘下来的这种水果大约经过多长时间后失去50%新鲜度()
A.33小时 B.35小时
C.38小时 D.43小时
2.已知函数是定义域为的奇函数,当,当,(为常数),若,则实数
A. B.
C. D.
3.设函数,且,则
A. B.1
C. D.3
4.已知函数,则
A. B.
C. D.
5.若函数的图象如图所示,则函数的图象大致是
A. B.
C. D.
6.设实数,且,,,则x,y,z的大小关系为
A. B.
C. D.
7.求函数f(x)=lg(x2-2x-3)的单调递减区间
A. B.
C. D.
8.函数的定义域为
A. B.
C. D.
9.函数的定义域为
A. B.
C. D.
10.函数与(且)在同一坐标系中的图象可以是
A. B.
C. D.
11.设,,,则,,大小关系为
A. B.
C. D.
12.设,,,则,,大小关系为
A. B.
C. D.
13.已知,则
A. B.
C. D.
14.函数的单调增区间是
A. B.
C. D.
15.已知,则以下结论中正确的是
A.; B.;
C.; D..
16.已知对数函数,且在区间上恒有,则实数a的取值范围是
A.; B.;
C.; D..
17.已知,,,则
A. B.
C. D.
18.函数f(x) = 1n(x2 - 2x - 8)的单调递增区间是
A.( - ,- 2) B.( - ,1 )
C.(1, + ) D.(4, + )
19.已知,那么等于
A. B.
C. D.
20.若实数a,b,c满足,则下列式子正确的是
A. B.
C. D.
21.已知,则的值为
A. B.
C. D.
22.设,则.
A. B.
C. D.
23.设2a=5b=m,且=2,则m等于
A. B.10
C. D.20
24.已知函数是定义在R上的偶函数,且在上单调递减,则下列三个数,,,的大小关系为
A. B.
C. D.
25.已知,,,则有
A. B.
C. D.
26.中国古代十进制的算筹计数法在世界数学史上是一个伟大的创造.据史料推测,算筹最晚出现在春秋晚期战国初年,算筹计数的方法是个位、百位、万位……的数按纵式的数码摆出:十位、千位、十万位……的数按横式的数码摆出.如7738可用算筹表示.
纵式
横式
1-9这9个数字的纵式与横式的表示数码如图所示,则图片表示的结果和下列相同的是
A. B.
C. D.
27.声音大小(单位为分贝)取决于声波通过介质时,所产生的压力变化(简称声压,单位为 ).已知声音大小与声压 的关系式为,且根据我国《城市区域环境噪音标准》规定,在居民区内,户外白昼噪声容许标为50分贝,夜间噪声容许 标准为40分贝,则居民区内,户外白昼噪声容许标准的声压是户外夜间噪声容许标准的声压的( )倍
A. B.
C.10 D.20
28.若函数,则
A. B.
C. D.
29.将(且)转化为对数形式,其中错误的是
A. B.
C. D.
30.若实数x、y满足(,且),则的值为
A. B.2
C. D.1
31.函数的单调递增区间为
A. B.
C.(1,3) D.(-1,1)
32.对数函数(,且)与二次函数在同一坐标系内的图象可能是
A. B.
C. D.
33.已知函数区间上恒有,则实数a的取值范围是
A. B.
C. D.
34.已知函数在上单调递增,则实数a的取值范围为
A. B.
C. D.
35.若,,,则
A. B.
C. D.
36.已知函数在上单调递减,则实数a的取值范围是
A. B.
C. D.
37.设,, 则
A. B.
C. D.
38.酒驾是严重危害交通安全的违法行为.为了保障交通安全,国家有关规定:驾驶员血液中的酒精含量大于或等于,小于的驾驶行为为酒后驾车,及以上认定为醉酒驾车.假设某驾驶员喝了一定量的酒后,其血液中的酒精含量上升到了.如果停止喝酒后,他血液中酒精含量会以每小时30%的速度减少,那么他至少经过( )小时才能驾驶.(参考数据,)
A.3 B.5
C.7 D.9
39.已知函数的表达式为.若且,则的取值范围为
A. B.
C. D.
40.如果在实数运算中定义新运算“”:.那么对于任意实数a、b、c,以下结论中不一定成立的是
A. B.
C. D.
二、多选题
1.下列指数式与对数式的互化中正确是
A.100=1与lg1=0 B.=与log27=-3
C.log39=2与32=9 D.log55=1与51=5
2.若,,则下列表达正确的是
A. B.
C. D.
3.声强级(单位:)与声强(单位:)之间的关系是,其中指的是人能听到的最低声强,对应的声强级称为闻阈.人能承受的最大声强为,对应的声强级为,称为痛阈.某歌唱家唱歌时,声强级范围为(单位:).下列选项中正确的是
A.闻阈的声强级为
B.此歌唱家唱歌时的声强范围(单位:)
C.如果声强变为原来的倍,对应声强级也变为原来的倍
D.声强级增加,则声强变为原来的倍.
4.已知是偶函数,在上是减函数,则下列给出的的取值范围中,能使得成立的有
A. B.
C. D.
5.历史上数学计算方面的三大发明为阿拉伯数字、十进制和对数,常用对数曾经在化简计算上为人们做过重大贡献,而自然对数成了研究科学、了解自然的必不可少的工具.现有如下四个关于对数的运算,其中正确的是
A. B.
C. D.
6.若,则下列结论正确的是
A. B.
C. D.
7.已知,则
A. B.
C. D.
8.已知正实数x,y,z满足,则下列正确的选项有
A. B.
C. D.
9.下列指数式与对数式互化正确的是
A.与 B.与
C.与 D.与
10.已知函数,则
A.在上的最大值为 B.在上单调递增
C.在上无最小值 D.的图象关于直线对称
11.已知函数,下列四个命题正确的是.
A.函数为偶函数
B.若,其中,,,则
C.函数在上为单调递增函数
D.若,则
12.表示不超过的最大整数,下列说法正确的是
A.
B.,
C.
D.
13.已知正数、满足,则下列说法中正确的是
A. B.
C. D.
14.设都是正数,且,那么
A. B.
C. D.
15.已知互不相等的三个实数a,b,c都大于1,且满足,则a,b,c的大小关系可能是
A. B.
C. D.
三、填空题
1.已知,则用m表示____________.
2.函数的定义域为____________.
3.已知对数函数(且)的图象经过点,则实数____________.
4.已知,,且,则实数a的取值范围是____________.
5.已知函数,当时,函数的最大值比最小值大4,则实数____________.
6.计算:____________.
7.若,,且,则____________.
8.____________.
9.____________.
10.函数的定义域是____________.
11.已知常数且,假设无论a为何值,函数的图象恒经过一个定点,则这个点的坐标为____________.
12.函数的单调递增区间为____________.
13.已知在区间上单调递减,则实数的取值范围是____________.
14.函数的单调递减区间是____________.
15.已知,则关于x的不等式的解集是____________.
四、解答题
1.已知函数.
(1)若,求的值;
(2)记函数,求的值域.
2.设a、b、c是直角三角形的三边长,其中c为斜边长,且.求证:.
3.求下列各式的值:
(1);
(2);
(3);
(4).
4.已知函数.
(1)求函数的定义域;
(2)若,,求的值.
5.已知函数的表达式为
(1)求函数的定义域;
(2)若函数的最小值为,求实数a的值.
6.已知关系式(其中,,常数).若当时,取到最小值,求此时相应的的值.
7.我们常说的里氏震级,其计算公式为,其中是距震中处标准测震仪接收到的地震的最大振幅,是该处接收到的级地震波的最大振幅.某地区发生了级地震.随后的一次余震中,一个距离震中的测震仪接收到的地震最大振幅是,该处记录的级地震波的最大振幅是.
(1)求这次余震的震级(精确到);
(2)求前面发生的级地震的最大振幅是这次余震的多少倍(精确到).
8.酒驾是严重危害交通安全的违法行为.为了保障交通安全,根据国家有关规定:100mL血液中酒精含量达到20~79mg的驾驶员即为酒后驾车,80mg及以上认定为醉酒驾车.假设某驾驶员喝了一定量的酒后,其血液中的酒精含量上升到了1mg/mL.如果在停止喝酒以后,他血液中酒精含量会以每小时30%的速度减少,那么他至少经过几个小时才能驾驶?
高中人教A版 (2019)4.2 指数函数复习练习题: 这是一份高中人教A版 (2019)4.2 指数函数复习练习题,文件包含专题42指数函数解析版docx、专题42指数函数原卷版docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。
人教A版 (2019)必修 第一册4.4 对数函数同步训练题: 这是一份人教A版 (2019)必修 第一册4.4 对数函数同步训练题,文件包含专题42对数与对数函数解析版docx、专题42对数与对数函数原卷版docx等2份试卷配套教学资源,其中试卷共58页, 欢迎下载使用。
专题4.2 指数函数- 2022-2023学年高一数学阶段性复习精选精练(人教A版2019必修第一册): 这是一份专题4.2 指数函数- 2022-2023学年高一数学阶段性复习精选精练(人教A版2019必修第一册),文件包含专题42指数函数解析版docx、专题42指数函数原卷版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。