




北师大版七年级数学下册——专题2.2探索直线平行的条件专项提升训练
展开专题2.2探索直线平行的条件专项提升训练
班级:___________________ 姓名:_________________ 得分:_______________
注意事项:
本试卷满分120分,试题共24题,其中选择10道、填空6道、解答8道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2022春•沙坪坝区校级月考)图中,∠1和∠2不是同位角的是( )
A. B.
C. D.
2.(2022春•洞头区期中)如图,∠1和∠2是( )
A.同位角 B.内错角 C.对顶角 D.同旁内角
3.(2022春•常州期中)已知∠1与∠2是内错角,则( )
A.∠1=∠2 B.∠1+∠2=180°
C.∠1<∠2 D.以上都有可能
4.(2022春•顺德区校级期中)如图,下列判断正确的是( )
A.若∠1=∠2,则AD∥BC
B.若∠1=∠2,则AB∥CD
C.若∠A=∠3,则AD∥BC
D.若∠3+∠DAB=180°,则AB∥CD
5.(2022春•新乐市校级月考)如图,直线a,b被直线c所截,则∠5的同位角是( )
A.∠1 B.∠2 C.∠3 D.∠4
6.(2022•天津模拟)如图,在△ABC中,点D,E,F分别在边BC,AB,AC上,下列不能判定DE∥AC的条件是( )
A.∠3=∠C B.∠1+∠4=180° C.∠1=∠AFE D.∠1+∠2=180°
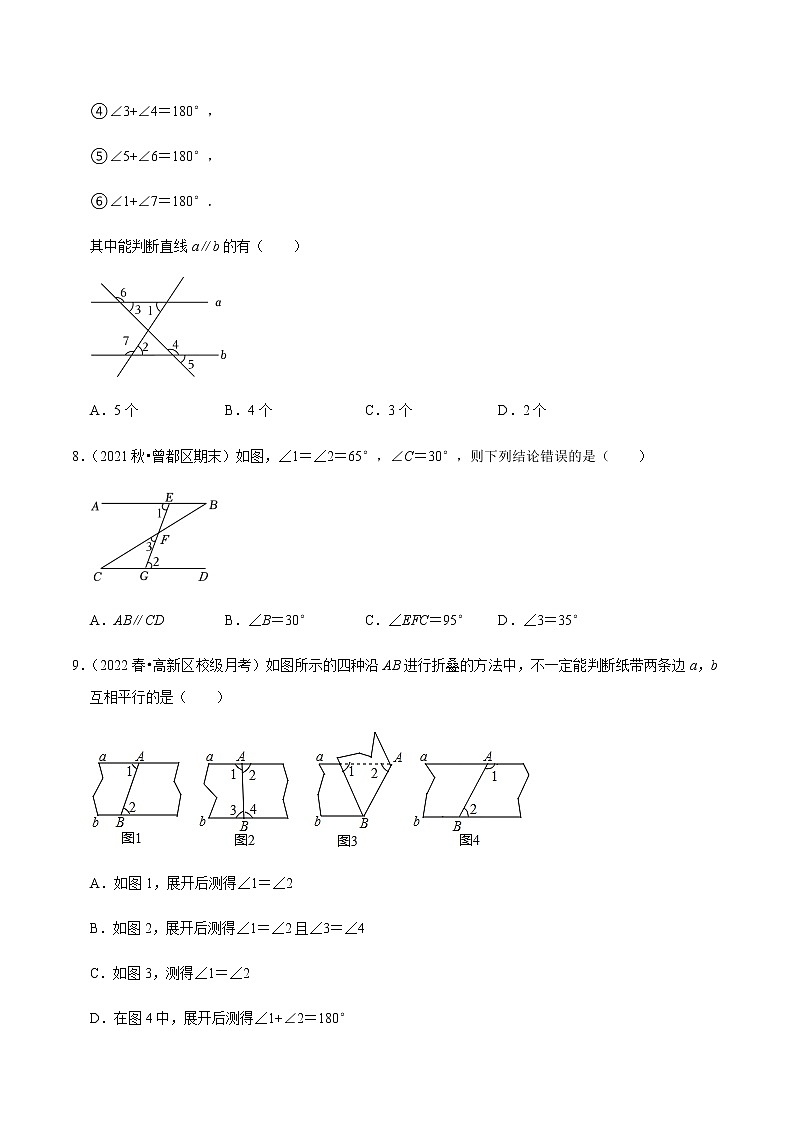
7.(2021秋•船山区期末)如图,有下列一些条件:
①∠1=∠2,
②∠2=∠3,
③∠4=∠6,
④∠3+∠4=180°,
⑤∠5+∠6=180°,
⑥∠1+∠7=180°.
其中能判断直线a∥b的有( )
A.5个 B.4个 C.3个 D.2个
8.(2021秋•曾都区期末)如图,∠1=∠2=65°,∠C=30°,则下列结论错误的是( )
A.AB∥CD B.∠B=30° C.∠EFC=95° D.∠3=35°
9.(2022春•高新区校级月考)如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2
B.如图2,展开后测得∠1=∠2且∠3=∠4
C.如图3,测得∠1=∠2
D.在图4中,展开后测得∠1+∠2=180°
10.(2022春•藁城区校级月考)某学员在驾校练习驾驶汽车,两次拐弯后的行驶方向与原来的方向相反,则两次拐弯的角度可能是( )
A.第一次向左拐30°,第二次向右拐30°
B.第一次向左拐45°,第二次向右拐135°
C.第一次向左拐60°,第二次向右拐120°
D.第一次向左拐53°,第二次向左拐127°
二、填空题(本大题共6小题,每小题3分,共18分)请把答案直接填写在横线上
11.(2021秋•晋江市期末)如图,直线AB,CD被AE所截,则∠A的内错角是 .
12.(2021秋•中牟县期末)如图,直线a,b被直线c所截,∠1=115°,∠2=65°.
∵∠1+∠2=115°+65°=180°,
∴a∥b( ).
13.(2022春•清镇市期中)在同一平面内有三条直线l1、l2、l3,若l1⊥l2,l2⊥l3,则l1与13的位置关系是 .
14.(2022•南京模拟)如图,四边形ABCD,点E在BC的延长线上,依据“内错角相等,两直线平行”来判断AD∥BC,可选择的一组内错角是 .(填一种答案即可)
15.(2022春•双峰县期末)如图,在下列给出的条件中,可以判定AD∥BC的有 .
①∠ADB=∠DBC
②∠DBC=∠DAC
③∠DBC=∠ACB
④∠DAB+∠ABC=180°
⑤∠DCB+∠ABC=180°
16.(2022春•丽水期末)如图,平面反光镜AC斜放在地面AB上,一束光线从地面上的P点射出,DE是反射光线.已知∠APD=120°,若要使反射光线DE∥AB,则∠CAB应调节为 度.
三、解答题(本大题共8小题,共72分.解答时应写出文字说明、证明过程或演算步骤)
17.(2020春•澧县期末)分别指出下列图中的同位角、内错角、同旁内角.
18.(2019春•河池期末)(经典题)如图所示,完成下列填空.
(1)∵∠1=∠5(已知)
∴a∥ (同位角相等,两直线平行);
(2)∵∠3= (已知)
∴a∥b(内错角相等,两直线平行);
(3)∵∠5+ =180°(已知)
∴ ∥ (同旁内角互补,两直线平行).
19.(2021春•济南期末)填写下列空格:
已知:如图,CE平分∠ACD,∠AEC=∠ACE.
求证:AB∥CD.
证明:∵CE平分∠ACD(已知),
∴∠ =∠ ( ).
∵∠AEC=∠ACE(已知),
∴∠AEC=∠ ( ).
∴AB∥CD( ).
20.(2018春•邵阳县期末)如图,已知∠1=∠2 求证:a∥b.
21.(2017春•个旧市月考)如图,∠2+∠D=180°,∠1=∠B,那么AB∥EF吗?为什么?
22.(2021秋•峄城区期末)如图,已知点E在BD上,AE⊥CE且EC平分∠DEF.
(1)求证:EA平分∠BEF;
(2)若∠1=∠A,∠4=∠C,求证:AB∥CD.
23.(2022•苏州模拟)已知如图所示,∠B=∠C,点B、A、E在同一条直线上,∠EAC=∠B+∠C,且AD平分∠EAC,试说明AD∥BC的理由.
24.(2022•南京模拟)已知:如图所示,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
(1)求证:AB∥CD;
(2)试探究∠2与∠3的数量关系.









