9.4 向量应用（四大题型）-高一数学新教材同步配套教学讲义（苏教版必修第二册）

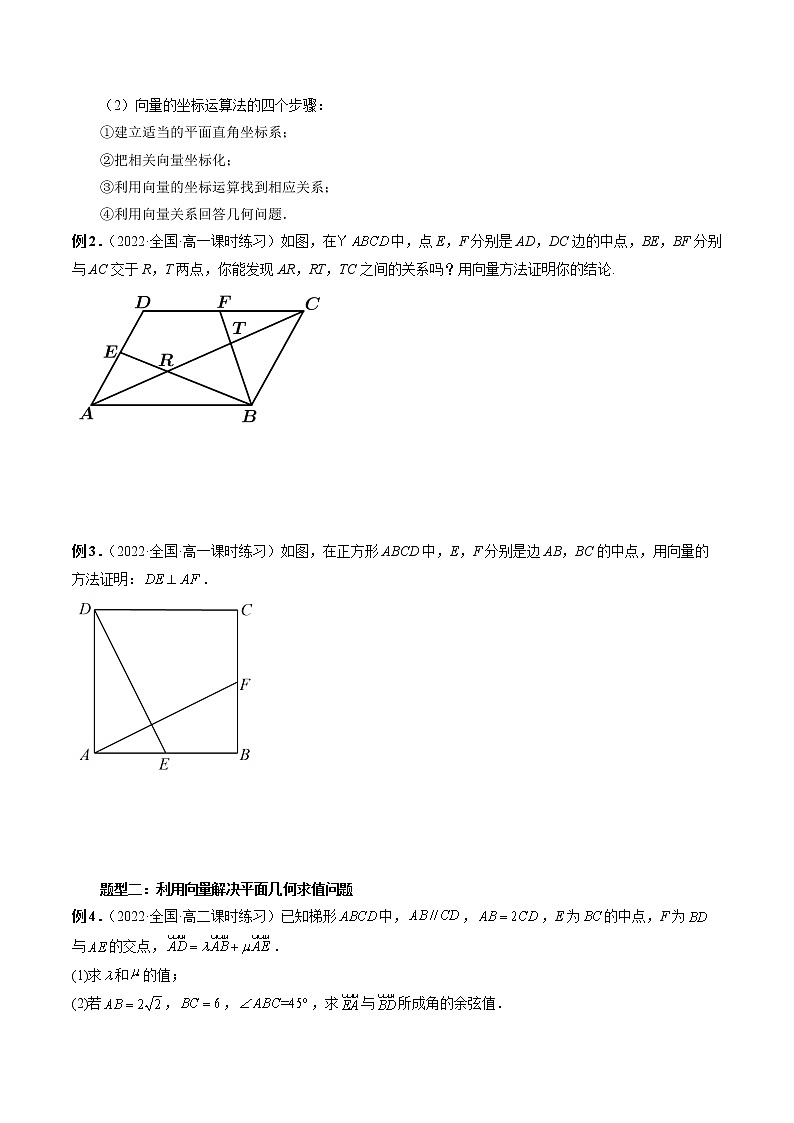
9．4 向量应用【题型归纳目录】题型一：利用向量证明平面几何问题题型二：利用向量解决平面几何求值问题题型三：向量在物理中的应用题型四：平面几何中的平行（共线）问题【知识点梳理】知识点一：向量方法解决平面几何问题的步骤用向量方法解决平面几何问题的“三步曲”：（1）建立平面几何与向量的联系，用向量表示问题中涉及的几何元素，将平面几何问题转化为向量问题．（2）通过向量运算，研究几何元素之间的关系，如距离、夹角等问题．（3）把运算结果“翻译”成几何关系．知识点二：向量方法解决物理问题的步骤用向量方法讨论物理学中的相关问题，一般来说分为四个步骤：（1）问题转化，即把物理问题转化为数学问题．（2）建立模型，即建立以向量为载体的数学模型．（3）求解参数，即求向量的模、夹角、数量积等．（4）回答问题，即把所得的数学结论回归到物理问题．【典型例题】题型一：利用向量证明平面几何问题例1．（2022·全国·高一课时练习）用向量方法证明：菱形对角线互相垂直．已知四边形是菱形，，是其对角线．求证：．【方法技巧与总结】用向量证明平面几何问题的两种基本思路（1）向量的线性运算法的四个步骤：①选取基底；②用基底表示相关向量；③利用向量的线性运算或数量积找到相应关系；④把计算所得结果转化为几何问题．（2）向量的坐标运算法的四个步骤：①建立适当的平面直角坐标系；②把相关向量坐标化；③利用向量的坐标运算找到相应关系；④利用向量关系回答几何问题．例2．（2022·全国·高一课时练习）如图，在中，点E，F分别是AD，DC边的中点，BE，BF分别与AC交于R，T两点，你能发现AR，RT，TC之间的关系吗？用向量方法证明你的结论.例3．（2022·全国·高一课时练习）如图，在正方形ABCD中，E，F分别是边AB，BC的中点，用向量的方法证明：．题型二：利用向量解决平面几何求值问题例4．（2022·全国·高二课时练习）已知梯形中，，，E为的中点，F为与的交点，．(1)求和的值；(2)若，，，求与所成角的余弦值．【方法技巧与总结】（1）用向量法求长度的策略①根据图形特点选择基底，利用向量的数量积转化，用公式求解．②建立坐标系，确定相应向量的坐标，代入公式：若，则．（2）用向量法解决平面几何问题的两种思想①几何法：选取适当的基底（基底中的向量尽量已知模或夹角），将题中涉及的向量用基底表示，利用向量的运算法则、运算律或性质求解．②坐标法：建立平面直角坐标系，实现向量的坐标化，将几何问题中的长度、垂直、平行等问题转化为代数运算．例5．（2022·重庆·高一期末）如图，在中，已知，，点在上，且，点是的中点，连接，相交于点.(1)求线段，的长；(2)求的余弦值.例6．（2022·辽宁·沈阳市奉天高级中学高一期中）如图，在中，D是的中点，.(1)若，求；(2)若，求的值.变式1．（2022·全国·高一课时练习）已知菱形ABCD的三个顶点，，，求：(1)第四个顶点D的坐标；(2)菱形ABCD的面积．题型三：向量在物理中的应用例7．（2022·全国·高一专题练习）三个大小相同的力、、作用在同一物体上，使物体沿方向做匀速运动，设，，，判断的形状．【方法技巧与总结】用向量解决物理问题的一般步骤（1）问题的转化，即把物理问题转化为数学问题．（2）模型的建立，即建立以向量为主体的数学模型．（3）参数的获得，即求出数学模型的有关解——理论参数值．（4）问题的答案，即回到问题的初始状态，解释相关的物理现象．例8．（2022·全国·高一专题练习）如图，长江某地南北两岸平行，江面的宽度d＝1 km，一艘游船从南岸码头A出发航行到北岸．假设游船在静水中的航行速度的大小为 ，水流速度的大小为 ，设和的夹角为，北岸在A的正北方向．(1)当时，判断游船航行到北岸时的位置是在图中的左侧还是右侧，并说明理由．(2)当多大时，游船能到达处？需航行多长时间？例9．（2022·湖南·高一课时练习）如图，一物体在表面粗糙的斜面上不动，斜面沿水平方向做匀速直线运动，若物体的质量为，斜面的倾角为，位移大小为s，求物体与斜面之间的摩擦力所做的功．题型四：平面几何中的平行（共线）问题例10．（2022·陕西宝鸡·高一期末）如图，已知分别是的三条高，试用向量的方法求证：相交于同一点．【方法技巧与总结】利用向量方法可以解决平面几何中的平行（共线）等问题，有两种思路：一种思路是选择一组基底，利用基向量表示涉及的向量，另一种思路是建立坐标系，求出题目中涉及的向量的坐标．例11．（2022·全国·高一课时练习）如图，点O是平行四边形的中心，分别在边上，且，求证点在同一直线上.【同步练习】一、单选题1．（2022·山东·高一阶段练习）若平面上的三个力作用于一点，且处于平衡状态．已知，与的夹角为，则力的大小为（    ）．A．7 B． C． D．12．（2022·福建省厦门第二中学高二阶段练习）图为某种礼物降落伞的示意图，其中有根绳子和伞面连接，每根绳子和水平面的法向量的夹角均为．已知礼物的质量为，降落伞自身的重量为，每根绳子的拉力大小相同．则降落伞在匀速下落的过程中每根绳子拉力的大小为（    ）（重力加速度取，精确到）．A． B． C． D．3．（2022·全国·高三专题练习）在日常生活中，我们会看到两个人共提一个行李包的情况（如图所示）．假设行李包所受的重力为，所受的两个拉力分别为，，且，与的夹角为，则以下结论不正确的是（　　）A．的最小值为B．的范围为C．当时， D．当时，4．（2022·陕西渭南·高一期末）如图所示，一个物体被两根轻质细绳拉住，且处于平衡状态，已知两条绳上的拉力分别是，，且，与水平夹角均为，，则物体的重力大小为（    ）A． B． C． D．5．（2022·陕西·宝鸡市金台区教育体育局教研室高一期末）已知两个力，的夹角为，它们的合力大小为，合力与的夹角为，那么的大小为 （    ）A． B．C． D．6．（2022·全国·高二课时练习）已知力与水平方向的夹角为（斜向上），大小为，一个质量为的木块受力的作用在动摩擦因数的水平平面上运动了，则力和摩擦力所做的功分别为（    ）（）A．， B．， C．， D．，7．（2022·四川内江·高一期末（文））是边长为4的等边三角形，点D、E分别在边AC、BC上，且，则的最小值为（    ）A． B． C．3 D．－38．（2022·四川内江·高一期末（理））四边形ABCD中，，，，则的最小值为（    ）A． B． C．3 D．－3二、多选题9．（2022·全国·高一课时练习）（多选）如图所示，小船被绳子拉向岸边，船在水中运动时，设水的阻力大小不变，那么小船匀速靠岸过程中（    ）A．船受到的拉力不断增大 B．船受到的拉力不断变小C．船受到的浮力不断变小 D．船受到的浮力保持不变10．（2022·广东佛山·高一期末）一物体受到3个力的作用，其中重力的大小为4N，水平拉力的大小为3N，另一力未知，则（    ）A．当该物体处于平衡状态时，B．当与方向相反，且时，物体所受合力大小为C．当物体所受合力为时，D．当时，11．（2022·湖南·岳阳一中一模）已知正方形的对角线长为，是它的内切圆一条弦，点为正方形四条边上的一个动点，当弦的长度最大时，不可能为（    ）A． B． C． D．12．（2022·全国·高一期末）一物体受到3个力的作用，其中重力的大小为，水平拉力的大小为，力未知，则（    ）A．当该物体处于平衡状态时，ΝB．当物体所受合力为时，ΝC．当时，D．当时，必存在实数，使得 三、填空题13．（2022·上海市洋泾中学高三阶段练习）如图，已知是半径为圆心角为的一段圆弧上的一点，若，则的取值范围是__________． 14．（2022·广东·佛山市南海区南海执信中学高二开学考试）已知为内一点，且满足，则为的________心．15．（2022·全国·高一课时练习）已知，两个力作用于同一个质点，使点从点移到点，则对质点做的功______（即与的数量积）．16．（2022·全国·高一课时练习）已知，，现有动点P从开始，沿着与向量相同的方向做匀速直线运动，速度大小为每秒，另一动点Q从开始，沿着与向量相同的方向做匀速直线运动，速度大小为每秒，设P，Q在时分别在，处，则当时所需的时间t为______s.四、解答题17．（2022·全国·高一课时练习）如图，在平行四边形中，已知，，对角线，试用向量的方法求对角线的长．18．（2022·山东枣庄·高一期末）在中，是线段的靠近点的三等分点．(1)用表示；(2)求的长度．19．（2022·上海市延安中学高一阶段练习）如图，在直角三角形ABC中，，，，，，其中，，设DE中点为M，AB中点为N．(1)若，求证：C、M、N三点共线；(2)若，求的最小值．20．（2022·江苏·连云港高中高一期中）在直角坐标平面内，已知向量，，，为满足条件（）的动点．当取得最小值时，求：(1)向量的坐标；(2)的值；(3)求点A到直线的距离．21．（2022·福建·高一期中）如图，设Ox、Oy是平面内相交成角的两条数轴，分别是与x轴，y轴正方向同向的单位向量，若向量，则把有序数对叫做向量在坐标系xOy中的坐标，设.(1)计算的大小；(2)甲在Ox上距O点3千米的点A处，乙在Oy上距O点1千米的点B处，现在甲沿的方向，乙沿的方向同时以4千米/小时的速度行走；①若过半小时后甲到达C点，乙到达D点，请用与来表示；②若t时刻，甲到达G点，乙到达H点，求的最小值.22．（2022·湖南·高一课时练习）如图，已知点O为平面直角坐标系的原点，点A的坐标为（4，3），点B的坐标为（－1，6），作，垂足为点D．(1)求，，；(2)求；(3)求．