





沪科版九年级上册22.2 相似三角形的判定课堂教学ppt课件
展开相似三角形平行线截三角形相似的定理利用角的关系判定三角形相似定理边角关系判定三角形相似定理三边关系判定三角形相似定理直角三角形相似的判定
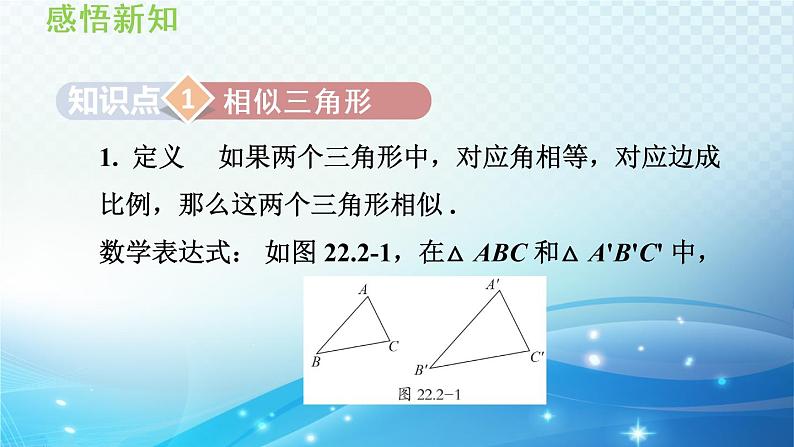
1. 定义 如果两个三角形中,对应角相等,对应边成比例,那么这两个三角形相似 .数学表达式: 如图 22.2-1,在△ ABC 和△ A'B'C' 中,
2. 相似三角形的表示方法 相似用符号“∽”表示,读作“相似 于 ” . 如 图 22.2-2, △ ABC 与 △ A'B'C' 相 似, 记 作 “△ ABC ∽△ A'B'C'”,读作“△ ABC 相似于△ A'B'C'” .
特别警示:用符号“ ∽” 表示两个三角形相似时,要把 表示对应顶点的大写字母写在对应的位置上 .△ ABC ∽ △ A'B'C' 表 示 顶 点 A 与 A', B 与 B', C 与 C' 分别对应;如果仅说“△ ABC 与△ A'B'C' 相似”,没有用 “∽”连接,则需要分类讨论它们顶点的对应关系 .
特别解读相似三角形的定义可以作为相似三角形的判定方法,也是相似三角形最重要的性质 . 相似三角形具有传递性,即若△ABC∽△A′B′C′,△ A′ B′ C′∽△ A″ B″ C″,则△ ABC ∽△ A″ B″ C″ .
如图 22.2-3,已知△ ABC ∽△ ADE,∠ A=70°,∠ B=40°, AB=6, BC=6, AD=3.
解题秘方:紧扣“相似三角形定义中对应角相等,对应边成比例”求解 .
(1)求△ ABC 与△ ADE 的相似比;
(2)求∠ AED 的度数和 DE 的长 .
特别提醒利用相似三角形对应角相等,对应边成比例解决问题时,应明确相似三角形顶点的对应关系 .本题中, 因为△ ABC ∽△ ADE,所以点 A 与点 A 对应、点 B与点 D 对应、点 C 与点E 对应 .
平行线截三角形相似的定理
1. 定理 平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似 .数学表达式: 如图 22.2-4 所示,∵ DE ∥ BC,∴△ ABC ∽△ ADE.
2. 作用 本定理是相似三角形判定定理的预备定理,它通过平行证三角形相似,再由相似证对应角相等、对应边成比例 .
特别提醒:1. 书写两个三角形相似时,要把表示对应顶点的大写字母写在对应的位置上 .2. 根据定理得到的相似三角形的三个基本图形中都有 BC ∥ DE,图 22.2 - 4 ①②很像大写字母 A, 故我们称之为“A” 型相似;图 22.2 - 4 ③很像大写字母 X,故我们称之为“X”型相似 ( 也像阿拉伯数字“8”).
如图 22.2-5,已知在 ABCD 中, E 为 AB 延长线上的一点, AB=3BE, DE 与 BC 相交于点 F,请找出图中各对相似三角形,并求出相应的相似比 .
解题秘方:紧扣“平行线截三角形两边的两种基本图形——‘ A’型和‘ X’型” 进行查找 .
解:∵四边形 ABCD 是平行四边形,∴ AB ∥ CD, AD ∥ BC, AB=CD.∴△ BEF ∽△ CDF,△ BEF ∽△ AED.∴△ BEF ∽△ CDF ∽△ AED.∵ AB=3BE,∴△ BEF ∽△ CDF,
特别提醒:由 ABCD 可 知AB ∥ CD,AD ∥ BC, 再根据平行线截三角形相似的定理及相似三角形的传递性找相似三角形,得 到 △ BEF, △ CDF,△ AED 都相似,共构成三对相似三角形 .求相似比不仅要找准对应边,还要注意两个三角形的先后次序,若次序颠倒,则相似比为原来相似比的倒数 .
[中考·上海 ]《九章算术》中记载了一种测量井深的方法.如图 22.2-6 所示,在井口 B 处立一根垂直于井口的木杆BD,从木杆的顶端 D 观察井水水岸 C,视线 DC 与井口的直径 AB 交于点 E,如果测得 AB=1.6 m, BD=1 m, BE=0.2 m,那么 AC 为 ________m.
解题秘方:判断是用平行线截线段成比例,还是用平行线截三角形相似的对应边成比例解题是关键 .
教你一招利用平行线求线段长的方法:对于被平行线所截形成“A”型或“X”型的图形,当所求的线段或已知线段在平行的边上时,通常考虑通过证三角形相似,再利用相似三角形的对应边成比例构建包含已知与未知线段的比例式,即可求出线段的长;当所求的线段或已知线段不在平行的边上时,则考虑直接用平行线截线段成比例求线段的长 .
利用角的关系判定三角形相似定理
1. 定理 如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似(可简单说成: 两角分别相等的两个三角形相似) .数学表达式: 如图 22.2-7 所示,在△ ABC 和△ DEF 中,∵∠ A= ∠ D,且∠ B= ∠ E,∴△ ABC ∽△ DEF.
特别提醒由两组角分别相等判定两个三角形相似,其关键是找准对应角.一般地,相等的角是对应角.如:公共角、对顶角、同角(等角)的余角(补角)等都是相等的角,解题时要注意挖掘题目中的隐含条件 .
2. 常见的相似三角形的类型(1)平行线型:如图 22.2-8 ①,若 DE ∥ BC,则△ ADE ∽△ ABC;(2)相交线型:如图 22.2-8 ②,若∠ AED= ∠ B,则△ AED ∽△ ABC;
(3) “子母”型:如图 22.2-8 ③,若∠ ACD= ∠ B,则△ ACD ∽△ ABC;(4) “K ”型:如 图 22.2-8 ④,若 点 A, C, D 共 线, 且∠ A=∠ D =∠ BCE=90°,则△ ACB ∽△ DEC,图形整体像一个横放的字母 K ,所以称为“K ”型相似 .
如图 22.2-9,在△ ABC 中, AD 是∠ BAC 的平分线, AD 的垂直平分线交 AD 于点 E,交 BC 的延长线于点 F. 求证:△ ABF ∽△ CAF.
解题秘方:紧扣“两角分别相等的两个三角形相似”,如图 22.2-9, 由于∠ BFA 是公共角,因此只需说明∠ B =∠ 4 即可证明 .
思路点拨当两个三角形已具备一角对应相等的条件时,往往先找是否有另一角对应相等 . 找角相等时 , 应注意挖掘公共角、对顶角、同角的余角 ( 或补角 ) 等隐含条件 .
证明: ∵ EF 垂直平分 AD,∴ AF=DF. ∴∠ FAD = ∠ 3.∵∠ B = ∠ 3 -∠ 1,∠ 4 = ∠ FAD -∠ 2,∠ 1 = ∠ 2,∴∠ B = ∠ 4.又∵∠ BFA = ∠ AFC,∴△ ABF ∽△ CAF.
边角关系判定三角形相似定理
定理 如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似(可简单说成: 两边成比例且夹角相等的两个三角形相似) .
特别提醒运用该定理证明相似时,一定要注意边角的关系,相等的角一定是 成 比 例 的 两 组 对 应边的夹角 . 类似于判定三 角 形 全 等 的 SAS 的方法 .
解题秘方:紧扣“两边成比例且夹角相等的两个三角形相似”证明三角形相似,再根据相似三角形的对应边成比例解决问题.
三边关系判定三角形相似定理
定理 如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似(可简单说成: 三边成比例的两个三角形相似) .
特别提醒由三边成比例判定两三角形相似的方法与三边对应相等判定三角形全等的方法类似,只需把三边对应相等改为三边成比例即可 .应用时要注意比的顺序性,即分子为同一个三角形的三边,分母为另一个三角形的三边,同时要注意边的对应情况,用大边对大边、小边对小边的思路找对应边 .
图 22.2-13、图 22.2-14 中小正方形的边长均为 1,则图 22.2-14 中的哪一个三角形(阴影部分)与图 22.2-13 中的△ ABC 相似?
解题秘方:根据网格的特征用勾股定理求出三角形各边的长,紧扣“三边成比例的两个三角形相似”,用计算比较法判断 .
解法提醒利用三边成比例判定两三角形相似的方法:先把两个三角形的边分别按照从小到大的顺序排列,找出两个三角形的对应边;再分别计算小、中、大三组对应边的比 ;最后看三个比的比值是否相等,若相等,则两个三角形相似,否则不相似 .
1. 定理 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似(可简单说成:斜边和一组直角边对应成比例的两个直角三角形相似) .
2. 直角三角形相似的判定方法(1)一组锐角相等的两个直角三角形相似;(2)两组直角边对应成比例的两个直角三角形相似;(3)斜边和一组直角边对应成比例的两个直角三角形相似 .
思路点拨判定两三角形相似的思路:1. 已知平行于三角形一边的直线,直接找两个三角形相似;2. 已知一角对应相等,找另一角对应相等,或夹这个角的两边对应成比例;3. 已知两边对应成比例,找夹角相等,或与第三边成比例;4.已知直角三角形,找一组锐角相等,或两组直角边对应成比例,或斜边和一组直角边对应成比例 .
在 Rt △ ABC 和 Rt △ DEF 中,∠ C = ∠ F=90°,下列条件中 , 不能判定这两个三角形相似的是( )A. ∠ A=55°,∠ D=35°B. AC=9, BC=12, DF=6, EF=8C. AC=3, BC=4, DF=6, DE=8D. AB=10, AC=8, DE=15, EF=9
解题秘方:紧扣“直角三角形相似的判定方法”一一进行验证 .
解法提醒两直角三角形相似的判定方法:一组锐角相等或两组直角边对应成比例或斜边和一组直角边对应成比例 .
活学巧记证相似,比线段,添线平行成习惯;一证两对角相等,或证三边成比例;两边成比也能用,夹角相等才可行 .
初中数学22.2 相似三角形的判定一等奖课件ppt: 这是一份初中数学22.2 相似三角形的判定一等奖课件ppt,共35页。PPT课件主要包含了学习目标,新课导入,新课讲解,课堂小结,当堂小练,拓展与延伸,布置作业等内容,欢迎下载使用。
初中数学第22章 相似形22.2 相似三角形的判定备课ppt课件: 这是一份初中数学第22章 相似形22.2 相似三角形的判定备课ppt课件,共22页。PPT课件主要包含了学习目标,复习引入,合作探究,符号语言,典例精析,练一练,答案不相似等内容,欢迎下载使用。
2020-2021学年第22章 相似形22.2 相似三角形的判定课前预习ppt课件: 这是一份2020-2021学年第22章 相似形22.2 相似三角形的判定课前预习ppt课件,共22页。PPT课件主要包含了学习目标,不相似,合作探究,符号语言,典例精析,练一练等内容,欢迎下载使用。













