



初中数学北师大版七年级下册4 用尺规作三角形教学ppt课件
展开类型一 已知两边对应相等 方法1 寻找第三边对应相等,用“SSS” 1.如图,在四边形ABCD中,AB=CD,AD=BC,E,F分别是AB,CD的中点,连接AF,CE,且AF=CE,试说明:∠B=∠D.
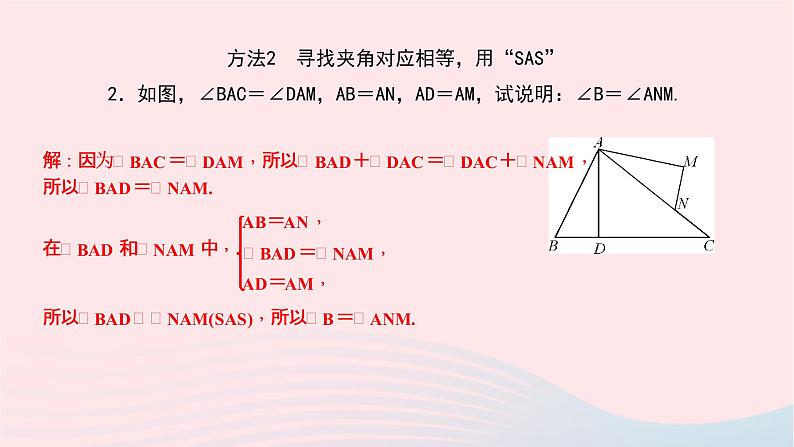
方法2 寻找夹角对应相等,用“SAS” 2.如图,∠BAC=∠DAM,AB=AN,AD=AM,试说明:∠B=∠ANM.
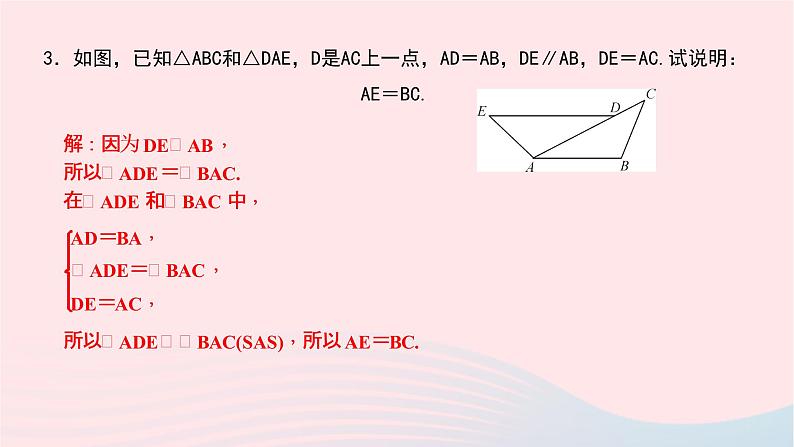
3.如图,已知△ABC和△DAE,D是AC上一点,AD=AB,DE∥AB,DE=AC.试说明:AE=BC.
类型二 已知一边一角对应相等 方法1 已知一边和该边的邻角对应相等,寻找夹该角的另一边对应相等,用“SAS” 4.如图,点C,F,E,B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,写出CD与AB之间的关系,并证明你的结论.
方法2 已知一边和该边的邻角对应相等,寻找另一角对应相等,用“AAS”或“ASA” 5.如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.试说明:BE=CD.
6.如图,AB∥CD,E是CD上一点,BE交AD于点F,EF=BF.试说明:AF=DF.
方法3 已知一边和该边的对角对应相等,寻找另一角对应相等,用“AAS” 7.如图,CA=CD,∠B=∠E,∠BCE=∠ACD.试说明:AB=DE.
8.如图,AD是△ABC的中线,分别过点B,C作直线AD的垂线,垂足分别为E,F.试说明:BE=CF.
类型三 已知两角对应相等 方法1 寻找夹边对应相等,用“ASA” 9.如图,点D在△ABC的BC边上,DE∥AC交AB于点E,DF∥AB交AC于点F.试说明:AE=DF.
10.如图,在△ABC中,EF∥BC,PG∥AB,AP=CF,试说明:△AEF≌△PGC. 解:因为EF∥BC,PG∥AB, 所以∠C=∠AFE,∠GPC=∠A. 因为AP=CF, 所以AP+PF=CF+PF, 即AF=PC, 所以△AEF≌△PGC(ASA).
人教版八年级上册数学作业课件 证明三角形全等的基本思路 (共20张PPT): 这是一份人教版八年级上册数学作业课件 证明三角形全等的基本思路 (共20张PPT)
初中第13章 全等三角形综合与测试习题ppt课件: 这是一份初中第13章 全等三角形综合与测试习题ppt课件,共19页。
北师大版七年级下册第四章 三角形5 利用三角形全等测距离教学课件ppt: 这是一份北师大版七年级下册第四章 三角形5 利用三角形全等测距离教学课件ppt,共11页。













