人教版八年级上册11.2.2 三角形的外角精品精练

专训11.1.2 三角形外角和问题

一、单选题

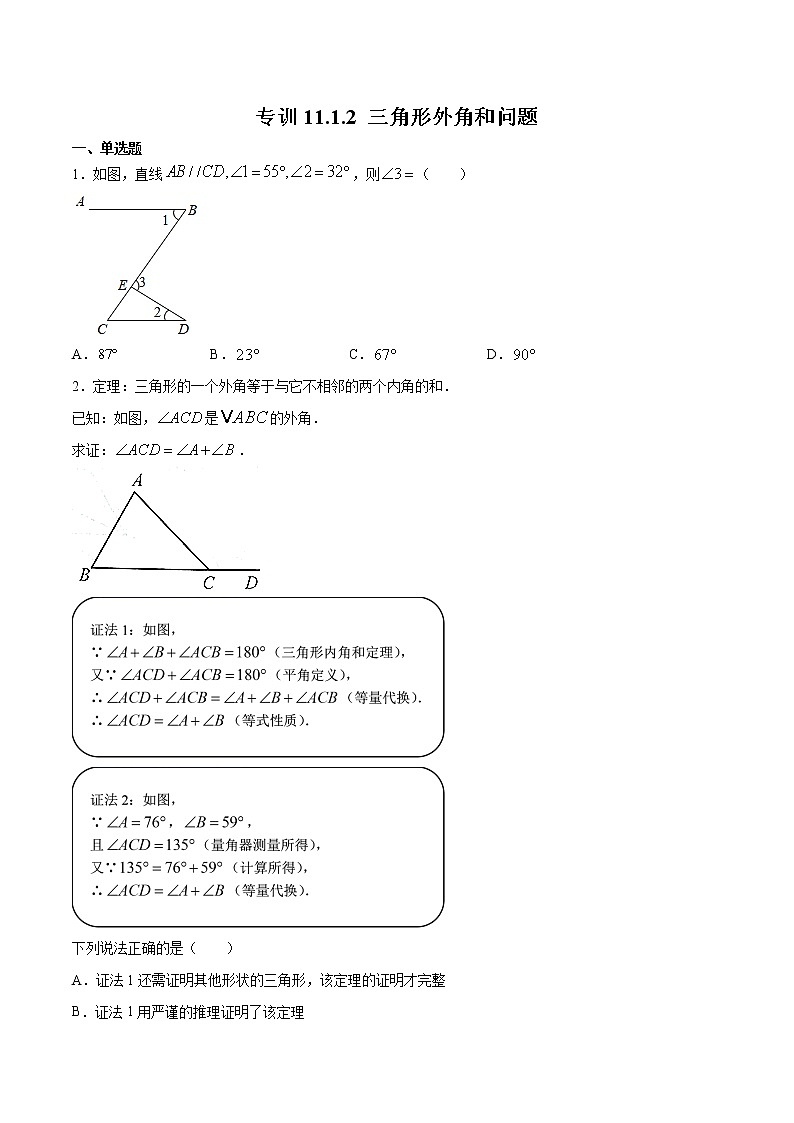
1．如图，直线，则（    ）

A． B． C． D．

【答案】A

【分析】

利用平行线的性质得到，再利用三角形外角的性质即可求解．

【详解】

解：∵，

∴，

∴，

故选：A．

【点睛】

本题考查平行线的性质、三角形外角的性质，掌握上述基本性质定理是解题的关键．

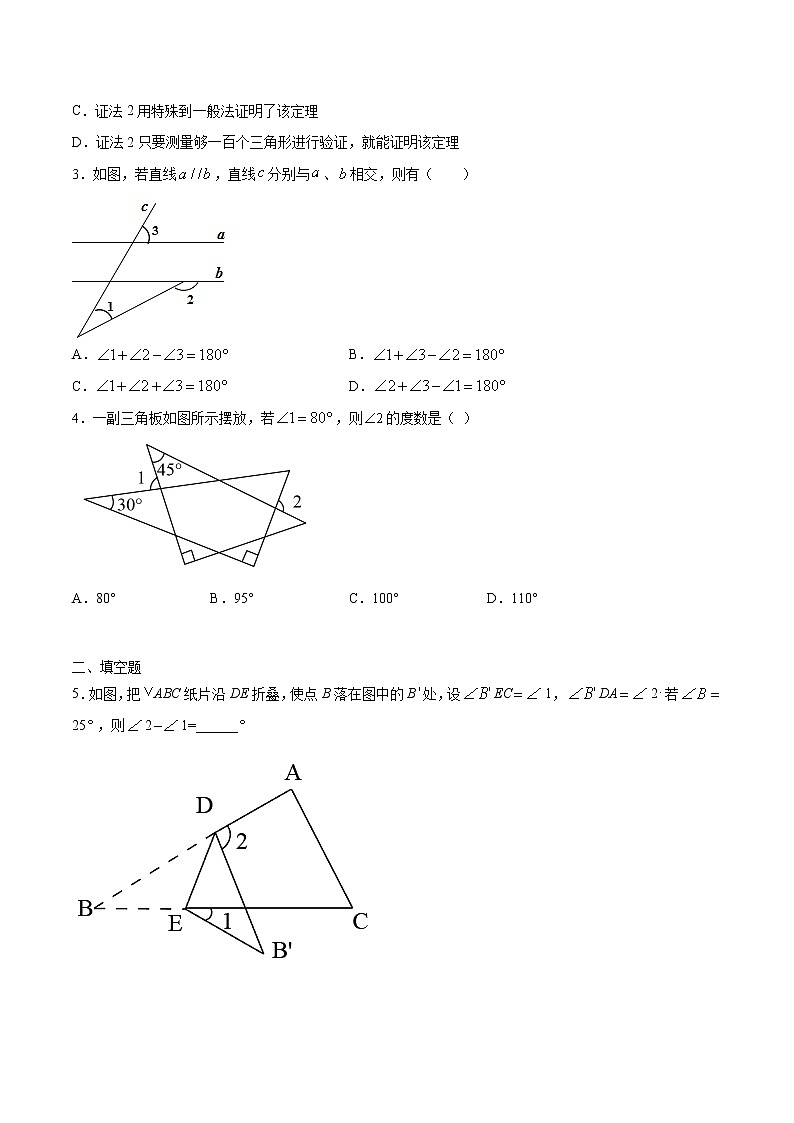
2．定理：三角形的一个外角等于与它不相邻的两个内角的和．

已知：如图，是的外角．

求证：．

下列说法正确的是（    ）

A．证法1还需证明其他形状的三角形，该定理的证明才完整

B．证法1用严谨的推理证明了该定理

C．证法2用特殊到一般法证明了该定理

D．证法2只要测量够一百个三角形进行验证，就能证明该定理

【答案】B

【分析】

根据三角形的内角和定理与平角的定义可判断A与B，利用理论与实践相结合可判断C与D．

【详解】

解：A. 证法1给出的证明过程是完整正确的，不需要分情况讨论，故A不符合题意；

B. 证法1给出的证明过程是完整正确的，不需要分情况讨论，故选项B符合题意；

C. 证法2用量角器度量两个内角和外角，只能验证该定理的正确性，用特殊到一般法证明了该定理缺少理论证明过程，故选项C不符合题意；

D. 证法2只要测量够一百个三角形进行验证，验证的正确性更高，就能证明该定理还需用理论证明，故选项D不符合题意．

故选择：

【点睛】

本题考查三角形外角的证明问题，命题的正确性需要严密推理证明，三角形外角分三种情形，锐角、直角、和钝角，证明中应分类才严谨．

3．如图，若直线，直线分别与、相交，则有（    ）

A． B．

C． D．

【答案】D

【分析】

先利用平行线的性质以及邻补角的关系求得∠5=180°-∠4=180°-∠3，再利用三角形的外角性质即可求解．

【详解】

解：∵a//b，

∴∠4=∠3，

∴∠5=180°-∠4=180°-∠3，

∵∠2=∠1+∠5，

∴∠2=∠1+∠180°-∠3，

∴∠2+∠3-∠1+180°．

故选：D．

【点睛】

本题考查了平行线的性质三角形的外角性质，解题的关键是掌握：三角形的外角等于与它不相邻的两个内角之和．

4．一副三角板如图所示摆放，若，则的度数是（ ）

A．80° B．95° C．100° D．110°

【答案】B

【分析】

由三角形的外角性质得到∠3=∠4=35°，再根据三角形的外角性质求解即可．

【详解】

解：如图，∠A=90°-30°=60°，

∵∠3=∠1-45°=80°-45°=35°，

∴∠3=∠4=35°，

∴∠2=∠A+∠4=60°+35°=95°，

故选：B．

【点睛】

本题考查了三角形的外角性质，正确的识别图形是解题的关键．

二、填空题

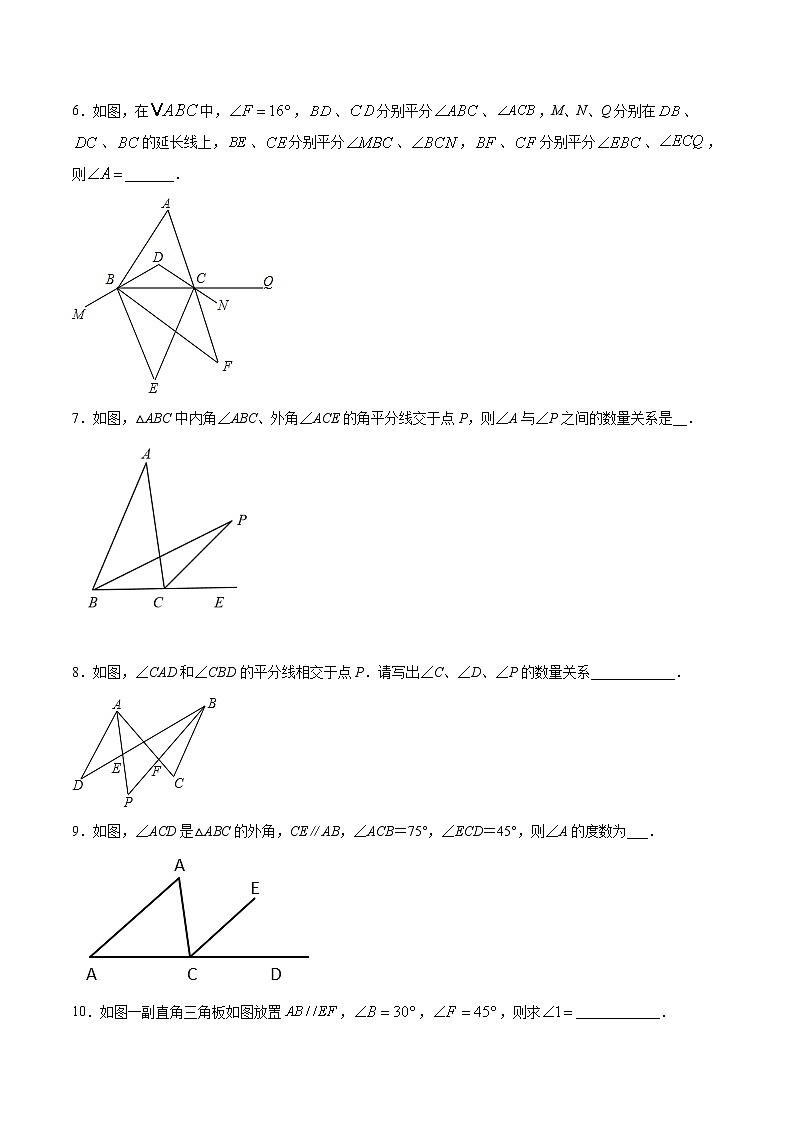
5．如图，把ABC纸片沿DE折叠，使点B落在图中的B处，设EC1，DA2若25，则21=______

【答案】50

【分析】

由折叠性质求得，由三角形的外角性质，用表示 ，进而求得．

【详解】

解：，

，

，

，

，

故答案为50．

【点睛】

本题主要考查三角形外角的性质，折叠的性质，关键是根据三角形的外角的性质表示出与的关系式．

6．如图，在中，，、分别平分、，M、N、Q分别在、、的延长线上，、分别平分、，、分别平分、，则_______．

【答案】52°

【分析】

根据三角形外角的性质和角平分线的定义可求出∠E，利用三角形内角和求出，得到，从而求出，再次利用角平分线的定义和三角形内角和得到∠A．

【详解】

解：、分别平分、，

，，

，，

即，，

，

、分别平分、，

，，

，

，

∴，

∴，

、分别平分、，

，，

∴，

，

故答案为：52°．

【点睛】

本题考查了三角形内角和定理、三角形外角性质、角平分线的定义等知识，解题的关键是灵活运用所学知识解决问题，属于中考选择题中的压轴题．

7．如图，△ABC中内角∠ABC、外角∠ACE的角平分线交于点P，则∠A与∠P之间的数量关系是__．

【答案】

【分析】

先根据三角形的外角性质得到，再根据角平分线的定义解答即可．

【详解】

解：∵是的一个外角，

∴，

∵是的角平分线，

∴，

∵是的角平分线，

∴，

∴，

故答案为：．

【点睛】

本题考查了三角形的外角性质、角平分线的定义，熟练掌握三角形的外角性质是解题关键．

8．如图，∠CAD和∠CBD的平分线相交于点P．请写出∠C、∠D、∠P的数量关系____________．

【答案】2∠P＝∠D+∠C

【分析】

根据三角形的外角性质、角平分线的定义得到∠CAD+∠P＝∠CBD+∠C，∠CAD+∠D＝∠CBD+∠P，两式相减整理即可．

【详解】

解：∵∠BFA＝∠PAC+∠P，∠BFA＝∠PBC+∠C，

∴∠PAC+∠P＝∠PBC+∠C，

∵∠CAD和∠CBD的平分线相交于点P，

∴∠PAC=∠PAD＝∠CAD，∠PBC=∠PBD＝∠CBD，

∴∠CAD+∠P＝∠CBD+∠C①，

∵∠DEP＝∠PAD+∠D，∠DEP＝∠EBP+∠P，

∴∠CAD+∠D＝∠CBD+∠P②，

①﹣②，得∠P﹣∠D＝∠C﹣∠P，

整理得，2∠P＝∠D+∠C，

故答案为：2∠P＝∠D+∠C．

【点睛】

本题考查角平分线定义，三角形外角性质，以及等式的性质，掌握角平分线定义，三角形外角性质，以及等式的性质是解题关键．

9．如图，∠ACD是△ABC的外角，CE∥AB，∠ACB＝75°，∠ECD＝45°，则∠A的度数为___．

【答案】60°

【分析】

根据∠ACB=75°，∠ ECD=45°可求得∠ACE的度数，再利用两直线平行，内错角相等的性质即可求解；

【详解】

∵∠ACB=75°，∠ ECD=45°

∴ ∠ACE=180°-75°-45°=60°，

又∵ CE∥AB，

∴∠A=∠ACE=60°，

故答案为：60°．

【点睛】

本题考查了平行线的性质，正确掌握知识点是解题的关键．

10．如图一副直角三角板如图放置，，，则求____________．

【答案】75°

【分析】

先根据平行线的性质，可得∠BAF=∠F=45°，再利用三角形外角的性质，即可得到答案．

【详解】

解：∵，

∴∠BAF=∠F=45°，

∴∠1=∠B+∠BAF=30°+45°=75°．

故答案是：75°．

【点睛】

本题主要考查平行线的性质以及三角形外角的性质，熟练掌握三角形外角的性质，是解题的关键．

11．如图，____________．

【答案】

【分析】

根据三角形外角的性质可得∠BAC=∠C+∠E，∠DAE=∠B+∠D，根据平角的定义即可得答案．

【详解】

∵∠BAC和∠DAE分别是△ACE和△ABD的外角，

∴∠BAC=∠C+∠E，∠DAE=∠B+∠D，

∴∠CAD+∠BAC+∠DAE=180°，

故答案为：180°

【点睛】

本题考查三角形外角性质，三角形的一个外角等于与它不相邻的两个内角的和；熟练掌握外角性质是解题关键．

12．将一副三角板如图摆放，斜边AB与直角边DE相交于点F，则_______．

【答案】

【分析】

先根据等腰直角三角形，求出∠DAE，再求出∠FAE，利用三角形外角性质即可求解．

【详解】

解：∵△ADE为等腰直角三角形，

∴∠DAE=∠E=45°，

又∵∠CAB=30°，

∴∠FAE=∠DAE-∠CAB=45°-30°=15°，

∴∠BFE=∠E+∠FAE=45°+15°=60°．

故答案为：60°．

【点睛】

本题考查三角板形成的角，等腰直角三角形性质，角的和差，三角形外角性质，掌握三角板形成的角，等腰直角三角形性质，角的和差，三角形外角性质是解题关键．

13．下图是可调躺椅示意图（数据如图），与的交点为，且，，保持不变．为了舒适，需调整的大小，使，则图中应___________（填“增加”或“减少”）___________度．

【答案】减少    10   

【分析】

先通过作辅助线利用三角形外角的性质得到∠EDF与∠D、∠E、∠DCE之间的关系，进行计算即可判断．

【详解】

解：∵∠A+∠B=50°+60°=110°，

∴∠ACB=180°-110°=70°，

∴∠DCE=70°，

如图，连接CF并延长，

∴∠DFM=∠D+∠DCF=20°+∠DCF，

∠EFM=∠E+∠ECF=30°+∠ECF，

∴∠EFD=∠DFM+∠EFM=20°+∠DCF+30°+∠ECF=50°+∠DCE=50°+70°=120°，

要使∠EFD=110°，则∠EFD减少了10°，

若只调整∠D的大小，

由∠EFD=∠DFM+∠EFM=∠D+∠DCF+∠E+∠ECF=∠D+∠E+∠ECD=∠D+30°+70°=∠ D+100°，

因此应将∠D减少10度；

故答案为：①减少；②10．

【点睛】

本题考查了三角形外角的性质，同时涉及到了三角形的内角和与对顶角相等的知识；解决本题的关键是理解题意，读懂图形，找出图形中各角之间的关系以及牢记公式建立等式求出所需的角，本题蕴含了数形结合的思想方法．

14．如图，于C，E是上一点，,平分平分，则：与之间的数最关系为______．

【答案】2∠H+∠ACF=180°

【分析】

延长EC，交DH于K，根据三角形外角的性质，平行线的性质即可得到90°+∠ACE=45°+∠ACE+∠H，从而求得∠ACE，进而即可求得∠H与∠ACF之间的数量关系．

【详解】

解：延长EC，交DH于K，

∵∠EKD=∠HEC+∠H，∠ECD=∠EKD+∠HDC，

∴∠ECD=∠HEC+∠HDC+∠H，

∵DF∥AB，

∴∠B=∠BDG，

∵EH平分∠BEC，DH平分∠BDG，

∴∠HEC=∠BEC，∠HDC=∠B，

∵∠BEC=∠A+∠ACE，

∴∠HEC=∠A+∠ACE，

∴∠ECD=∠A+∠ACE+∠B+∠H，

∵AC⊥BD，

∴∠A+∠B=90°，

∴∠ECD=45°+∠ACE+∠H，

∵AC⊥BD，

∴∠ECD=90°+∠ACE，

∴90°+∠ACE=45°+∠ACE+∠H，

∴90°+∠ACE=2∠H，

∴90°+（90°-∠ACF）=2∠H，即2∠H+∠ACF=180°，

故答案为：2∠H+∠ACF=180°．

【点睛】

本题考查了平行线的性质，角平分线的定义以及三角形外角的性质，是基础题．

15．已知，，将一副三角板按照如图方式摆放在平行线之间，且线段BC落在直线MN上，线段DE落在直线PQ上，其中，，CO平分，EO平分，两条角平分线相交与点O，则________．

【答案】52.5

【分析】

延长CO交PQ于点F，根据∠COE=∠CFE+∠OEF，结合平行线的性质，角的平分线的定义计算；

【详解】

延长CO交PQ于点F，则∠COE=∠CFE+∠OEF，

∵，，CO平分，EO平分，

∴∠BCF=30°，∠OEF=22.5°，

∵，

∴∠BCF=∠CFE，

∴∠COE=30°+22.5°=52.5°，

故答案为：52.5°．

【点睛】

本题考查了平行线的性质，角的平分线的定义，三角形外角定理，延长构造三角形外角，活用平行线的性质是解题的关键．

三、解答题

16．已知中，于点，平分，过点作直线，且，．

（1）求的外角的度数；

（2）求的度数．

【答案】（1）100°；（2）10°

【分析】

（1）根据平行线的性质、对顶角相等计算即可；

（2）根据角平分线的定义得到∠BAE=40°，根据平行线的性质求出∠GAD=90°，结合图形计算，得到答案．

【详解】

解：（1）∵GH∥BC，∠C=40°，

∴∠HAC=∠C=40°，

∵∠FAH=∠GAB=60°，

∴∠CAF=∠HAC+∠FAH=100°；

（2）∵∠HAC=40°，∠GAB=60°，

∴∠BAC=80°，

∵AE平分∠BAC，

∴∠BAE=40°，

∵GH∥BC，AD⊥BC，

∴∠GAD=90°，

∴∠BAD=90°-60°=30°，

∴∠DAE=∠BAE-∠BAD=10°．

【点睛】

本题考查的是三角形的外角性质、三角形内角和定理、角平分线的定义、平行线的性质，掌握三角形内角和定理、平行线的性质是解题的关键．

17．已知．

（1）若，求的度数．

（2）若，求证：．

【答案】（1）50°；（2）见解析

【分析】

（1）根据平行线的性质得出∠A+∠1+∠EBD=180°，代入求解即可；

（2）根据平行线的性质得到∠3=∠EBD，根据三角形外角的性质和已知可推出∠1=∠DEB，即可证明ED∥AC．

【详解】

（1）解：，

，

，，

；

（2）证明：，

，

，，

，，

，

．

【点睛】

本题考查了平行线的判定和性质，三角形外角性质的应用，能正确利用定理进行推理是解此题的关键．

18．如图，点D在AB上，点E在AC上，BE、CD相交于点O．

（1）若，，，求的度数；

（2）试猜想与之间的关系，并证明你猜想的正确性．

【答案】（1）30°；（2）∠BOC=∠A+∠B+∠C，证明见解析．

【分析】

（1）先利用三角形的外角性质求出∠BDO=90°，再利用三角形内角和定理即可求得∠B的度数；

（2）用三角形外角的性质，表示出∠BOC，∠BEC，等量代换最后得出结论．

【详解】

解：，，

；

，

；

．

理由：

，，

．

【点睛】

本题考查了三角形内角和定理和三角形外角的性质，解题关键是灵活应用三角形外角的性质．

19．如图，已知射线CB∥DA，∠C＝∠DAB＝120°，E，F在射线CB上，且满足DB平分∠ADF，DE平分∠CDF．

（1）求证：CD∥BA；

（2）若左右平移AB，则∠DEC﹣∠DBF和∠DEC+∠DBA的值是否会改变，若不变，求出它们的值，若改变，请说明理由．

【答案】（1）证明过程见解析；（2）不变，∠DEC﹣∠DBF=30°，∠DEC+∠DBA=90°．

【分析】

（1）根据平行线的性质和判定即可证明；
（2）先根据平行线的性质可得出∠DBF＝∠ADB，再利用角平分线的性质得出∠DEC﹣∠DBF＝∠EDB，从而得出答案．

【详解】

解：（1）∵CB∥DA，∠C＝∠DAB＝120°，

∴∠CDA＝180°﹣∠C＝180°﹣120°＝60°，

∴∠CDA+∠DAB＝180°，

∴CD∥BA；

（2）不变，理由如下：

∵CB∥DA，

∴∠DBF＝∠ADB，

∵DB平分∠ADF，

∴∠FDB＝∠ADB，

∴∠FDB＝∠ADB＝∠DBF，

∵DE平分∠CDF，

∴∠CDE＝∠FDE，

∴∠EDB＝∠FDE+∠FDB＝∠CDA＝×60°＝30°；

∴∠DEC﹣∠DBF＝∠EDB＝30°；

∵∠DBA＝∠ABC﹣∠DBF，

∴∠DEC+∠DBA＝∠DEC+60°﹣∠DBF＝30°+60°＝90°．

∴∠DEC﹣∠DBF和∠DEC+∠DBA的值不变，分别是30°和90°．

【点睛】

本题考查了平行线、角平分线的性质，解决本题的关键是掌握平行线的性质．

20．模型规律：如图1，延长交于点D，则．因为凹四边形形似箭头，其四角具有“”这个规律，所以我们把这个模型叫做“箭头四角形”．

模型应用

（1）直接应用：

①如图2，，则__________；

②如图3，__________；

（2）拓展应用：

①如图4，、的2等分线（即角平分线）、交于点，已知，，则__________；

②如图5，、分别为、的10等分线．它们的交点从上到下依次为、、、…、．已知，，则__________；

③如图6，、的角平分线、交于点D，已知，则__________；

④如图7，、的角平分线、交于点D，则、、之同的数量关系为__________．

【答案】（1）①110；②260；（2）①85；②110；③142；④∠B-∠C+2∠D=0

【分析】

（1）①根据题干中的等式直接计算即可；

②同理可得∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠DOE，代入计算即可；

（2）①同理可得∠BO1C=∠BOC-∠OBO1-∠OCO1，代入计算可得；

②同理可得∠BO7C=∠BOC-（∠BOC-∠A），代入计算即可；

③利用∠ADB=180°-（∠ABD+∠BAD）=180°-（∠BOC-∠C）计算可得；

④根据两个凹四边形ABOD和ABOC得到两个等式，联立可得结论．

【详解】

解：（1）①∠BOC=∠A+∠B+∠C=60°+20°+30°=110°；

②∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠DOE=2×130°=260°；

（2）①∠BO1C=∠BOC-∠OBO1-∠OCO1

=∠BOC-（∠ABO+∠ACO）

=∠BOC-（∠BOC-∠A）

=∠BOC-（120°-50°）

=120°-35°

=85°；

②∠BO7C=∠BOC-（∠BOC-∠A）

=120°-（120°-50°）

=120°-10°

=110°；

③∠ADB=180°-（∠ABD+∠BAD）

=180°-（∠BOC-∠C）

=180°-（120°-44°）

=142°；

④∠BOD=∠BOC=∠B+∠D+∠BAC，

∠BOC=∠B+∠C+∠BAC，

联立得：∠B-∠C+2∠D=0．

【点睛】

本题主要考查了新定义—箭头四角形，利用了三角形外角的性质，还考查了角平分线的定义，图形类规律，解题的关键是理解箭头四角形，并能熟练运用其性质．