初中人教版11.2.2 三角形的外角优秀教案
展开第十一章 三角形
11.2.2三角形的外角
一、内容和内容解析
1.内容
理解三角形外角的定义以及三角形的外角和,掌握运用三角形外角的性质解题.
2.内容解析
教材由学生已经熟悉的三角形的内角和定理引入,然后探索三角形外角的性质。在呈现方式上采用“问题—探究—发现”的研究模式,并采用了拼图和数学说理两种方法,一方面,让学生通过剪剪拼拼,动手操作,探索发现有关结论,另一方面又加以简单的数学说理,使学生初步体会,要得到一个数学结论,可以采用观察实验的方法,还可以采用数学推导说理的方法,观察实验只能给我们带来一个直观形象的数学结论,而推导说理可以使我们进一步确信这一数学结论是否正确。
基于以上分析,确定本节课的教学重点是:三角形的外角性质.
二、目标和目标分析
1.目标
(1)理解三角形的外角,探索并掌握三角形的外角的两条性质;
(2)利用学过的定理论证这些性质;
(3)能利用三角形的外角性质解决实际问题。
2.目标分析
达成目标(1)的标志是:学生清晰地知道三角形的外角的定义并能找到三角形外角,目标(2)体现在学生能用三角形的内角和以及邻补角的性质推导出三角形内角和外角的性质;
目标(3)体现在可以利用三角形外角的性质去解决三角形中求角度的问题
三、教学问题诊断分析
八年级学生的特点是模仿能力强,喜欢动手,思维活跃,同时学生已经学过三角形的内角和定理,以及三角形的边、顶点、内角和等概念,这为本节课的学习打下了基础。在以往的学习中学生的动手实践、自主探索及合作探究能力都得到了一定的训练,这就为学生自主探索、动手实验、讨论交流、尝试说理做了准备。
学生的已有经验不同,学习情况不同,因此,在课堂教学上,,必须把能力分为阶梯式进行提高,对学生进行有层次能力的培养。
基于以上分析,确定本节课的教学难点是:运用三角形外角性质进行有关计算能准确地表达推理的过程和方法.
四、教学过程设计
一、复习回顾
复习本节课需要用到两个知识点:三角形的内角,三角形的内角和
创设情景,明确目标
你还记得“如何画已知角的邻补角”吗?让学生动手操作,画一画.在此基础上再提问:已知三角形的一个角,你能画出它的邻补角吗?从而引入课题.
二、三角形的外角
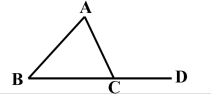
(1) 你能画出这个三角形的三个内角的所有邻补角吗?
展示点评:对比三角形的内角定义,给出三角形外角的定义,提问同一个三角形每一个内角有多少个邻补角,同一个三角形又多少个外角?小组讨论:三角形的高的交点位置有何特征?
反思小结:.三角形外角的特点:①顶点在三角形的一个顶点上。②一条边是三角形的一条边。③另一条边是三角形的某条边的延长线。
三角形外角的性质1
 活动二:任意画一个三角形,再画出它的所有外角,利用邻补角的性质求出相等的角和互补的角,你发现了什么?
活动二:任意画一个三角形,再画出它的所有外角,利用邻补角的性质求出相等的角和互补的角,你发现了什么?
∠1=∠2=180°-∠BAC,
∠3=∠4=180°-∠ABC,
∠5=∠6=180°-∠ACB.
三角形外角的性质2
活动三:
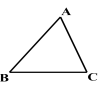
 如图,△ABC中,∠A=70°,∠B=60º,∠ACD是△ABC一个外角.
如图,△ABC中,∠A=70°,∠B=60º,∠ACD是△ABC一个外角.
- 能求出∠ACD吗?
- ∠ACD与∠A,∠B 有什么关系?
- ∠ACD与∠ACB 有什么关系?
展示点评:学生分组讨论,师生共同点评.
小组讨论:∠ACD的度数可以怎么求出?任意一个三角形都可以用这个方法求出它的外角吗?
反思小结:归纳:
①三角形的一个外角等于与它不相邻的 的和。
②三角形的一个外角大于任何一个 内角。
三、总结梳理,内化目标
 1.说出下列图形中∠1和∠2的度数:
1.说出下列图形中∠1和∠2的度数:
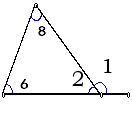
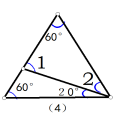 2、说出下列图形中∠3和∠4的度数:
2、说出下列图形中∠3和∠4的度数:
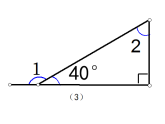
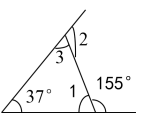 3、如图所示:
3、如图所示:
则∠1=_____;∠2=_____;∠3=______ .
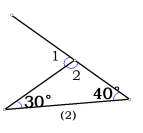
4、如图:∠1=25°,∠2=95°,∠3=30°,则∠4_______

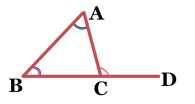 5、用“>”,“<”或“=”填空:
5、用“>”,“<”或“=”填空:
∠ACD ∠A
∠ACD ∠B
6、(1)∠1,∠2,∠3 分别是哪个三角形的外角?
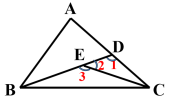 (2)∠1 ,∠3 和∠A 哪个大?
(2)∠1 ,∠3 和∠A 哪个大?
小结:
三角形的外角与内角的关系:
- 三角形的外角与它相邻的内角互补;
- 三角形的外角等于与它不相邻的两个内角的和;
- 三角形的一个外角大于任何一个与它不相邻的内角。
综合运用
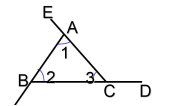
- 例4 如图,∠BAE,∠CBF,∠ACD的△ABC的三个外角,它们的和是多少?
2.三角形三个不同的外角的比为2:3:4,则这个三角形的三个内角分别是多少?
初中数学人教版八年级上册11.2.2 三角形的外角教学设计: 这是一份初中数学人教版八年级上册11.2.2 三角形的外角教学设计,共3页。教案主要包含了教学目标,教学准备,教学过设计等内容,欢迎下载使用。
初中数学人教版八年级上册11.2.2 三角形的外角教学设计: 这是一份初中数学人教版八年级上册11.2.2 三角形的外角教学设计,共2页。
人教版八年级上册11.2.2 三角形的外角教案设计: 这是一份人教版八年级上册11.2.2 三角形的外角教案设计,共2页。教案主要包含了学习目标,学法指导,课堂小结等内容,欢迎下载使用。