数学九年级下册5.1 二次函数教案

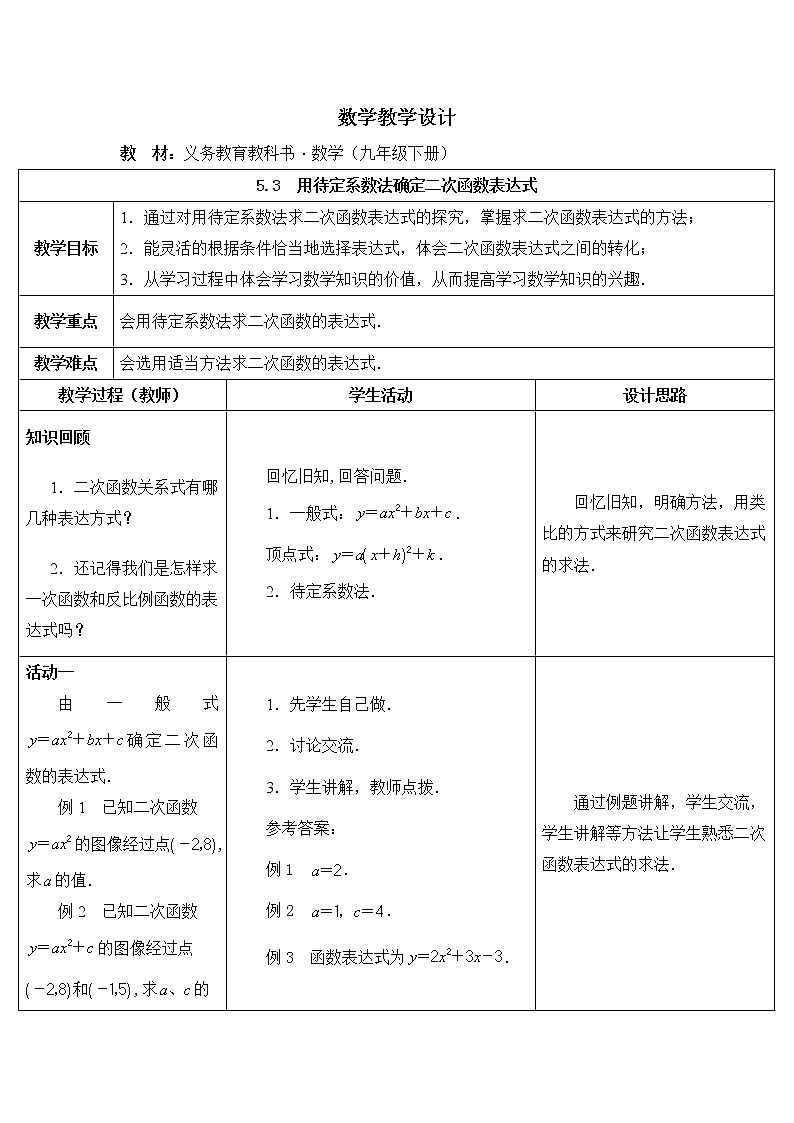
5.3　用待定系数法确定二次函数表达式

教学目标

1．通过对用待定系数法求二次函数表达式的探究，掌握求二次函数表达式的方法；

2．能灵活的根据条件恰当地选择表达式，体会二次函数表达式之间的转化；

3．从学习过程中体会学习数学知识的价值，从而提高学习数学知识的兴趣．

教学重点

会用待定系数法求二次函数的表达式．

教学难点

会选用适当方法求二次函数的表达式．

教学过程（教师）

学生活动

设计思路

知识回顾

1．二次函数关系式有哪几种表达方式？

2．还记得我们是怎样求一次函数和反比例函数的表达式吗？

回忆旧知,回答问题．

1．一般式：．

顶点式：．

2．待定系数法．

回忆旧知，明确方法，用类比的方式来研究二次函数表达式的求法．

活动一

由一般式确定二次函数的表达式．

例1　已知二次函数的图像经过点,求的值．

例2　已知二次函数的图像经过点和,求的值．

例3　已知二次函数的图像经过点和，求这个二次函数的表达式．

1．先学生自己做．

2．讨论交流．

3．学生讲解，教师点拨．

参考答案：

例1　．

例2　．

例3　函数表达式为．

通过例题讲解，学生交流，学生讲解等方法让学生熟悉二次函数表达式的求法．

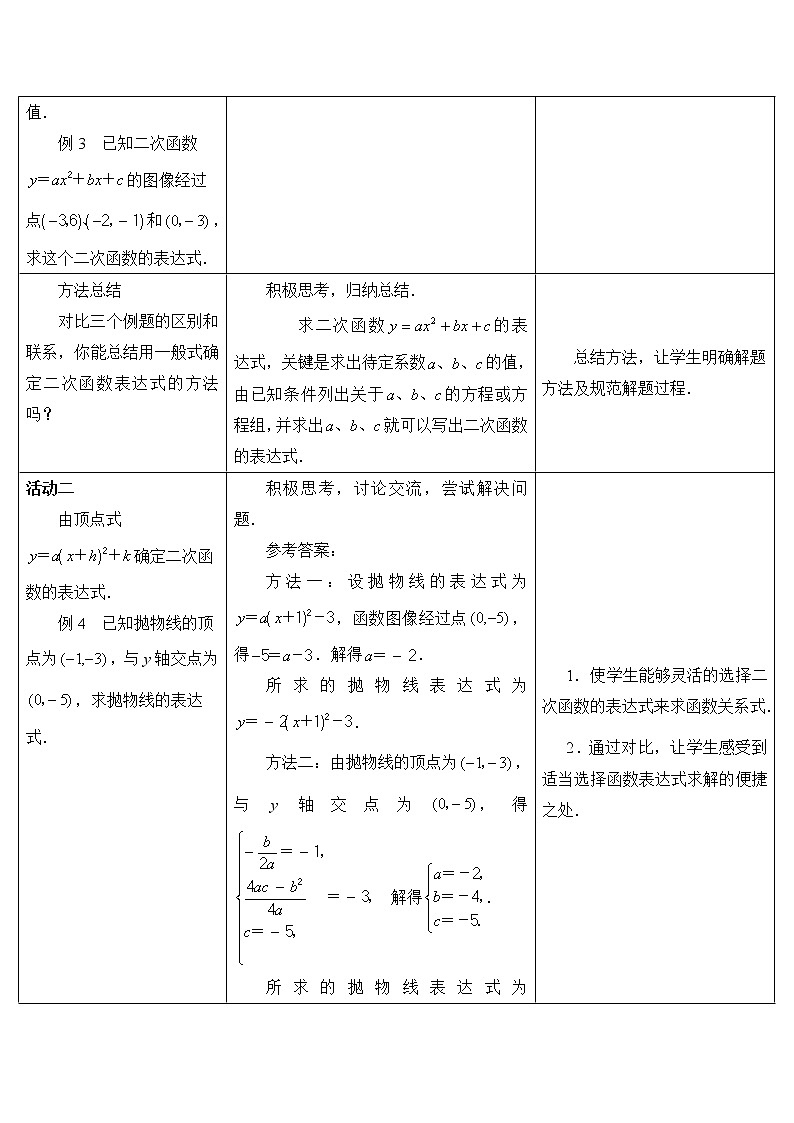
方法总结

对比三个例题的区别和联系，你能总结用一般式确定二次函数表达式的方法吗？

积极思考，归纳总结．

    求二次函数的表达式，关键是求出待定系数的值，由已知条件列出关于的方程或方程组，并求出就可以写出二次函数的表达式．

总结方法，让学生明确解题方法及规范解题过程．

活动二

由顶点式确定二次函数的表达式．

例4　已知抛物线的顶点为，与y轴交点为，求抛物线的表达式．

积极思考，讨论交流，尝试解决问题．

参考答案：

方法一：设抛物线的表达式为，函数图像经过点，得．解得．

所求的抛物线表达式为．

方法二：由抛物线的顶点为，与y轴交点为，得  　解得．

所求的抛物线表达式为．

学生可能还会有不同于以上解法的其他解法，教师可给予鼓励．

   1．使学生能够灵活的选择二次函数的表达式来求函数关系式．

   2．通过对比，让学生感受到适当选择函数表达式求解的便捷之处．

方法总结：

你能总结用顶点式求函数表达式的优点及方法吗？

积极思考，归纳总结．

    当给出的坐标或点中有顶点，可设顶点式，将h，k换为顶点坐标，再将另一点的坐标代入即可求出a的值．

总结方法，让学生明确解题方法及规范解题过程．

课堂练习

根据下列已知条件，选择合适的方法求二次函数的解析式：

1．已知二次函数的图像经过点和，求这个二次函数的表达式．

2．已知二次函数的图像经过原点，且当x＝1时，y有最小值－1，求这个二次函数的表达式．

拓展延伸：如图所示，已知抛物线的对称轴是过（3，0）的直线，它与x轴交于A、B两点，与y轴交于C点，点A、C的坐标分别是（8，0）、（0，4），求这个抛物线的表达式．

错误！未找到引用源。

　　部分学生板演，其余学生独立完成．

参考答案：

1．函数表达式为．

2．函数表达式为．

拓展延伸：抛物线表达式为．

在掌握了两类求二次函数关系式的方法和技巧的基础上，通过本组题的练习进一步提升学生根据不同条件，求二次函数关系式的能力．

课堂小结

你学到哪些二次函数表达式的求法？

师生共同总结：

1．已知图像上三点的坐标或给定x与y的三对对应值，通常选择一般式．

2．已知图像的顶点坐标，对称轴和最值，通常选择顶点式．确定二次函数的表达式时，应该根据条件的特点，恰当地选用一种函数表达方式．

让学生谈自己的感受，说出自己已掌握和领会的，或是还困惑的，促进学生反思与提高．

课后作业

课本习题5.3第1、2、3题．