

湘教版(2019)必修 第一册2.3 一元二次不等式导学案
展开
2.3 一元二次不等式
2.3.1 一元二次不等式及其解法
新课程标准解读
核心素养
1.经历从实际情境中抽象出一元二次不等式的过程,了解一元二次不等式的现实意义.能借助一元二次函数求解一元二次不等式,并能用集合表示一元二次不等式的解集
数学抽象、数学运算
2.借助一元二次函数的图象,了解一元二次不等式与相应函数、方程的联系
直观想象、数学建模
园艺师打算在绿地上用栅栏围一个矩形区域种植花卉.若栅栏的长度是24 m,围成的矩形区域的面积要大于20 m2.
[问题] 围成的这个矩形区域的边长应为多少米?
知识点一 一元二次不等式
1.把只含有一个未知数,并且未知数的最高次数是的不等式,称为一元二次不等式.
2.一元二次不等式的一般形式是ax2+bx+c>0或ax2+bx+c<0(其中a,b,c均为常数,a≠0).
对一元二次不等式的再理解
(1)一元,即只含一个未知数,其他元素均为常数(或参数);
(2)二次,即未知数的最高次数必须为2,且其系数不能为0.
下面所给关于x的几个不等式:①3x+4<0;②x2+mx-1>0;③ax2+4x-7>0;④x2<0.其中一定为一元二次不等式的有________.(填序号)
答案:②④
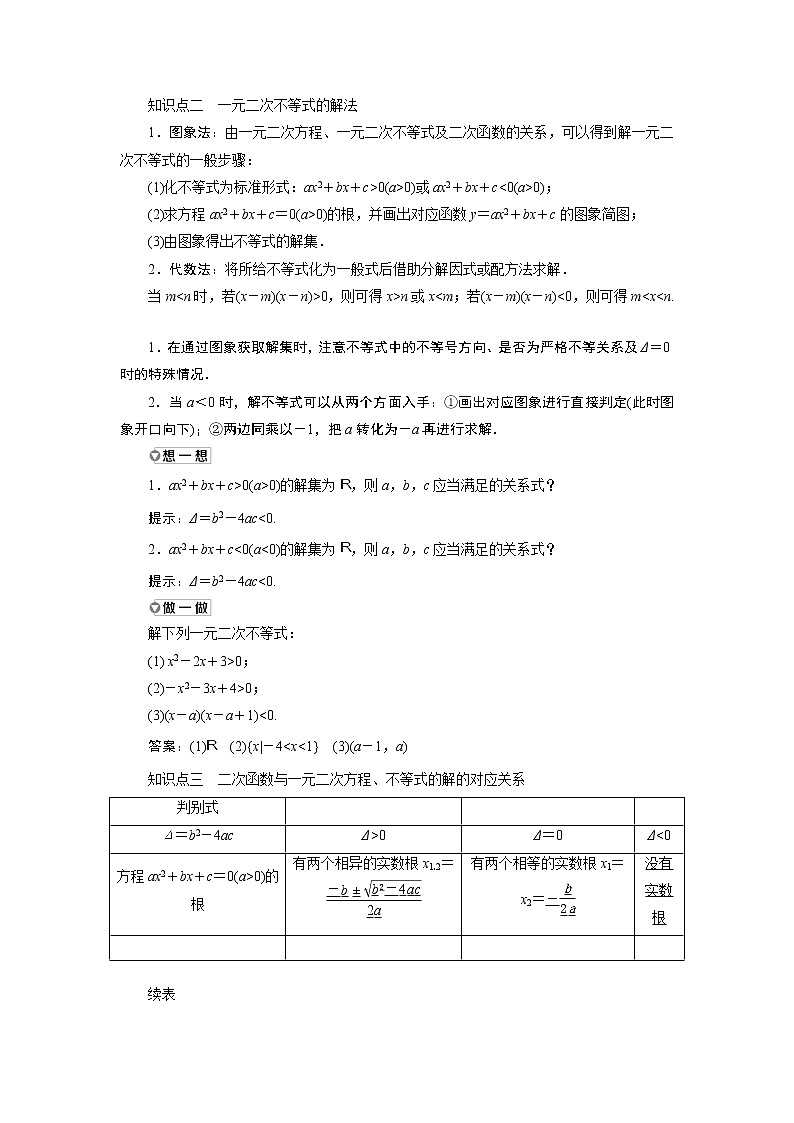
知识点二 一元二次不等式的解法
1.图象法:由一元二次方程、一元二次不等式及二次函数的关系,可以得到解一元二次不等式的一般步骤:
(1)化不等式为标准形式:ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0);
(2)求方程ax2+bx+c=0(a>0)的根,并画出对应函数y=ax2+bx+c的图象简图;
(3)由图象得出不等式的解集.
2.代数法:将所给不等式化为一般式后借助分解因式或配方法求解.
当m
1.在通过图象获取解集时,注意不等式中的不等号方向、是否为严格不等关系及Δ=0时的特殊情况.
2.当a<0时,解不等式可以从两个方面入手:①画出对应图象进行直接判定(此时图象开口向下);②两边同乘以-1,把a转化为-a再进行求解.
1.ax2+bx+c>0(a>0)的解集为R,则a,b,c应当满足的关系式?
提示:Δ=b2-4ac<0.
2.ax2+bx+c<0(a<0)的解集为R,则a,b,c应当满足的关系式?
提示:Δ=b2-4ac<0.
解下列一元二次不等式:
(1) x2-2x+3>0;
(2)-x2-3x+4>0;
(3)(x-a)(x-a+1)<0.
答案:(1)R (2){x|-4
判别式
Δ=b2-4ac
Δ>0
Δ=0
Δ<0
方程ax2+bx+c=0(a>0)的根
有两个相异的实数根x1,2=
有两个相等的实数根x1=x2=-
没有实数根
续表
判别式
Δ=b2-4ac
Δ>0
Δ=0
Δ<0
二次函数y=ax2+bx+c(a>0)的图象
二次函数y=ax2+bx+c(a>0)的零点
有两个零点x1,2=
有一个零点x=-
无零点
ax2+bx+c>0(a>0)的解集
(-∞,x1)∪(x2,+∞)
∪
ax2+bx+c<0(a>0)的解集
(x1,x2)
1.函数的角度:一元二次不等式ax2+bx+c>0表示二次函数y=ax2+bx+c的函数值大于0,图象在x轴的上方;一元二次不等式ax2+bx+c>0的解集即二次函数图象在x轴上方部分的自变量的取值范围.
2.方程的角度:一元二次不等式ax2+bx+c>0的解集的端点值是一元二次方程ax2+bx+c=0的根.
当Δ=0时,不等式ax2+bx+c≥0(a>0)与ax2+bx+c≤0(a>0)的解集分别是什么?
提示:R,.
1.不等式x(x-2)>0的解集为________,不等式x(x-2)<0的解集为________.
答案:{x|x<0或x>2} {x|0
一元二次不等式的解法
[例1] (链接教科书第51页例1、例2)解下列不等式:
(1)2x2+5x-3<0;
(2)-3x2+6x≤2;
(3)4x2+4x+1>0;
(4)-x2+6x-10>0.
[解] (1)Δ=49>0,方程2x2+5x-3=0的两根为x1=-3,x2=,
作出函数y=2x2+5x-3的图象,如图①所示.
由图可得原不等式的解集为.
(2)原不等式等价于3x2-6x+2≥0.Δ=12>0,解方程3x2-6x+2=0,得x1=,x2=,
作出函数y=3x2-6x+2的图象,如图②所示,由图可得原不等式的解集为.
(3)∵Δ=0,∴方程4x2+4x+1=0有两个相等的实根x1=x2=-.作出函数y=4x2+4x+1的图象如图③所示.
由图可得原不等式的解集为
.
(4)原不等式可化为x2-6x+10<0,
∵Δ=-4<0,
∴方程x2-6x+10=0无实根,
∴原不等式的解集为∅.
解形如ax2+bx+c>0或ax2+bx+c<0(其中a>0)的一元二次不等式,一般可分为三步:
(1)确定对应一元二次方程ax2+bx+c=0的根;
(2)画出对应二次函数y=ax2+bx+c的大致图象;
(3)由图象得出不等式的解集.
对于二次项系数是负数(即a<0)的一元二次不等式,可以先把二次项系数化为正数,再按上述步骤求解.
[跟踪训练]
解下列不等式:
(1)4x2-20x<-25;
(2)(x-3)(x-7)<0;
(3)-3x2+5x-4<0;
(4)x(1-x)≥x(2x-3)+1.
解:(1)不等式可化为4x2-20x+25<0,由于Δ=0,且对应的二次函数的图象是开口向上的抛物线,所以不等式的解集是∅.
(2)由题意知不等式对应方程的两个根是3和7,且对应的二次函数的图象是开口向上的抛物线,故不等式的解集是{x|3<x<7}.
(3)不等式-3x2+5x-4<0可化为3x2-5x+4>0,由于判别式Δ=25-48=-23<0,函数y=3x2-5x+4的图象开口向上,所以不等式的解集是R.
(4)不等式x(1-x)≥x(2x-3)+1可化为3x2-4x+1≤0.因为方程3x2-4x+1=0的两个根是,1,函数y=3x2-4x+1的图象开口向上,所以不等式的解集是
简单分式不等式的解法
[例2] (链接教科书第53页例4)解下列不等式:
(1)<0;(2)≤1.
[解] (1)<0⇔(x-3)(x+2)<0⇔-2
∴-1≤0,
∴≤0,
即≥0.
此不等式等价于(x-4)≥0且x-≠0,解得x<或x≥4,
∴原不等式的解集为.
1.对于比较简单的分式不等式,可直接转化为一元二次不等式或一元一次不等式组求解,但要注意分母不为零.
2.对于不等号右边不为零的较复杂的分式不等式,先移项再通分(不要去分母),使之转化为不等号右边为零,然后再用上述方法求解.
[跟踪训练]
解下列不等式:(1)≥0;(2)<3.
解:(1)根据商的符号法则,不等式≥0可转化成不等式组
解这个不等式组,可得x≤-1或x>3.
即原不等式的解集为{x|x≤-1,或x>3}.
(2)不等式<3可改写为-3<0,
即<0.
可将这个不等式转化成2(x-1)(x+1)<0,
解得-1
三个“二次”之间的关系
[例3] (链接教科书第54页例6)已知关于x的不等式ax2+5x+c>0的解集为.
(1)求a,c的值;
(2) 解关于x的不等式ax2+(ac+2)x+2c≥0.
[解] (1)由题意知不等式对应的方程ax2+5x+c=0的两个实数根为和,
且a<0,由根与系数的关系,得解得a=-6,c=-1.
(2)由a=-6,c=-1知不等式ax2+(ac+2)x+2c≥0可化为-6x2+8x-2≥0,即3x2-4x+1≤0,解得≤x≤1,所以不等式的解集为.
一元二次不等式解集逆向应用问题的解法及步骤
(1)求解方法:由已知不等式的解可转化为一元二次方程的两根,从而由根与系数的关系,找出系数a,b,c之间的关系,写出不等式的解集.
(2)求解步骤
第一步:审结论——明确解题方向:如要解cx2+bx+a<0,首先确定c的符号,最好能确定a,b,c的值;
第二步:审条件——挖掘题目信息:利用一元二次方程的根与一元二次不等式的解集的关系列出关于a,b,c的方程组,用a表示b,c;
第三步:建联系——找解题突破口:由给定不等式的解集形式→确定关于a,b,c的方程组→用a表示b,c→代入所求不等式→求解cx2+bx+a<0的解集.
[跟踪训练]
关于x的不等式ax-b>0的解集是{x|x>1},则关于x的不等式(ax+b)(x-3)>0的解集是( )
A.{x|-1<x<3} B.{x|1<x<3}
C.{x|x<1或x>3} D.{x|x<-1或x>3}
解析:选D 因为不等式ax-b>0的解集是{x|x>1},所以a>0,=1,所以(ax+b)(x-3)>0等价于a(x+1)(x-3)>0,其解集应为{x|x>3或x<-1},故选D.
一元二次不等式的实际应用
[例4] (链接教科书第53页例5)(1)“不等式x2-x+m>0在R上恒成立”的一个必要不充分条件是( )
A.m> B.0
(2)若对任意实数x,关于x的不等式(a2-1)x2-(a-1)x-1<0恒成立,则实数a的取值范围为________.
[解析] (1)若不等式x2-x+m>0在R上恒成立,则Δ=(-1)2-4m<0,解得m>,因此当不等式x2-x+m>0在R上恒成立时,必有m>0,但当m>0时,不一定推出不等式在R上恒成立,故所求的必要不充分条件可以是m>0.
(2)①若a2-1=0,则a=±1,
当a=1时,原不等式即为-1<0,解集为R.
当a=-1时,原不等式即为2x-1<0,解集为,与题意不符.
②若a≠±1,则当时,不等式解集为R,解得-
[答案] (1)C (2)
1.不等式ax2+bx+c>0的解是全体实数(或恒成立)的条件是:当a=0时,b=0,c>0;
当a≠0时,
2.不等式ax2+bx+c<0的解是全体实数(或恒成立)的条件是:当a=0时,b=0,c<0;
当a≠0时,
3.解决恒成立问题一定要搞清谁是主元,谁是参数.一般地,知道谁的范围,谁就是主元,求谁的范围,谁就是参数.
[跟踪训练]
已知关于x的不等式(m2+4m-5)x2-4(m-1)x+3>0对一切实数x恒成立,则实数m的取值范围为________.
解析:(1)当m2+4m-5=0,即m=1或m=-5时,显然m=1符合条件,m=-5不符合条件;
(2)当m2+4m-5≠0时,由二次函数对一切实数x恒为正数,
得解得1
答案:[1,19)
1.(多选)下列不等式是一元二次不等式的是( )
A.x2+x<-1 B.x2++1<0
C.x2++1<0 D.x2+1<0
解析:选AD 由于x2++1<0,x2++1<0不符合一元二次不等式的定义,只有x2+x<-1,x2+1<0是一元二次不等式,故选A、D.
2.不等式(x-1)2<x+5的解集为( )
A.{x|1<x<4} B.{x|-1<x<4}
C.{x|-4<x<1} D.{x|-1<x<3}
解析:选B 原不等式可化为x2-3x-4<0,即(x+1)(x-4)<0,故其解集为{x|-1<x<4}.故选B.
3.不等式x+>2的解集是( )
A.(-1,0)∪(1,+∞)
B.(-∞,-1)∪(0,1)
C.(-1,0)∪(0,1)
D.(-∞,-1)∪(1,+∞)
解析:选A 取x=-2,它不是不等式的解,排除B、D;取x=2,它是不等式的解,排除C.
4.当1
则有解得m≤-5.
答案:(-∞,-5]
高中数学湘教版(2019)必修 第一册2.3 一元二次不等式学案: 这是一份高中数学湘教版(2019)必修 第一册2.3 一元二次不等式学案,共12页。
湘教版(2019)必修 第一册2.3 一元二次不等式学案: 这是一份湘教版(2019)必修 第一册2.3 一元二次不等式学案,共13页。
高中数学湘教版(2019)必修 第一册1.1 集合导学案: 这是一份高中数学湘教版(2019)必修 第一册1.1 集合导学案,共6页。













