








初中数学湘教版七年级下册第3章 因式分解3.2 提公因式法课文配套ppt课件
展开3.2提公因式法(2)教案
课题 | 提公因式法(2) | 单元 | 3 | 学科 | 数学 | 年级 | 七 | |||
学习 目标 | 情感态度和价值观目标 | 通过观察能合理地进行分解因式的推导,并能清晰地阐述自己的观点 | ||||||||
能力目标 | 进一步培养学生的观察能力和类比推理能力. | |||||||||
知识目标 | 进一步让学生掌握用提公因式法分解因式的方法. | |||||||||
重点 | 能观察出公因式是多项式的情况,并能合理地进行分解因式 | |||||||||
难点 | 准确找出公因式,并能正确进行分解因式 | |||||||||
学法 | 自主探究,合作交流 | 教法 | 多媒体,问题引领 | |||||||
教学过程 | |
导入新课 | 提问:说说你如何理解公因式?
接着提问:公因式可以为多项式吗? |
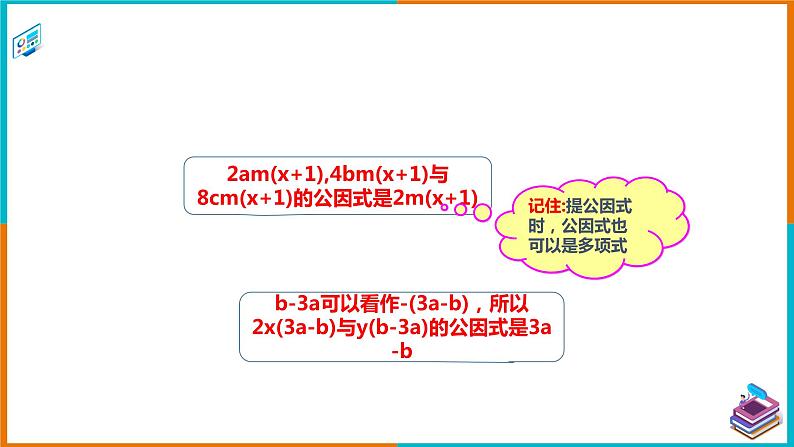
讲授新课 | 说一说 下列多项式中各项的公因式是什么? (1)2am(x+1)+4bm(x+1)+8cm(x+1) (2)2x(3a-b)-y(b-3a) 记住:提公因式时,公因式也可以是多项式.
做一做 在下列各式等号右边的括号前填入“+”或“-”号,使等式成立: (1)(a-b) =___(b-a); (2) (a-b)2 =___(b-a)2 (3) (a-b)3 =___(b-a)3;(4) (a-b)4 =___(b-a)4; (5) (a+b)5 =___(b+a)5;(6) (a+b)6 =___(b+a)6. (7) (a+b) =___(-b-a);(8) (a+b)2 =___(-a-b)2. 由此可知规律: (1)a-b 与b-a 互为相反数.(各项都互为相反数,则这两个多项式互为相反数) (a-b)n = (b-a)n (n是偶数) (a-b)n = -(b-a)n (n是奇数) (2)a+b 与 -a-b互为相反数.(偶次幂相等,奇次幂互为相反数),即若(n是整数) (-a-b)n = (a+b)n (n是偶数) (-a-b)n = -(a+b)n (n是奇数) (3) a+b与b+a互为相同数.(各项都相等,则这两个多形式相等) (a+b)n = (b+a)n (n是整数)
提问:两个只有符号不同的多项式是否有关系,有如下判断方法: (1)当相同字母前的符号相同时,则两个多项式相等 (2)当相同字母前的符号均相反时,则两个多项式互为相反数 例4、把下列多项式因式分解: (1) x(x-2)-3(x-2) (2) x(x-2)-3(2-x)
练习: 把下列各式进行因式分解: (1) a(m-6)+b(m-6) (2) 3(a-b)+a(b-a)
例5、把(a+c)(a-b)2-(a-c)(b-a)2分解因式 注意:第2项中的(b-a)2可以写成[-(a-b)]2 =(a-b)2.于是(a-b)2是各项的公因式. 练习: 把(x+y)(y-x)2-(x-y)3分解因式
例6、把12xy2(x+y)-18x2y(x+y)因式分解. 观察这个多项式,有什么特点?
议一议 因式分解时,如何确定多项式各项的公因式? 师生总结:当各项系数都是整数时,公因式的系数应取各项系数的(最大公约数);字母取各项的(相同字母),而且各字母的指数取最(小)次数。 |
巩固提升
| 1.因式分解2a(-a+b)2-(a-b)3,应提取的公因式是( ) A.-a+b B. a-b C.(a-b)2 D.以上都不对 答案:C 2.观察下列各式:①2a+b和a+b;②5m(a-b)和-a+b;③3(a+b)和-a+b;④2x2+2y2和x2+y2.其中有公因式的是( ) A.①② B.②③ C.③④ D.②④ 答案:D 3.多项式(x+y-z)(x-y+z)-(y+z-x)(z-x-y)各项的公因式为__________. 答案: x+y-z 4.已知a-1=b+c,则代数式a(a-b-c)-b(a-b-c)+c(b+c-a) 的值为__________. 答案: 1 5.化简求值: (3x-1)2(2x-3)-(3x -1)(2x-3)2-x(3x-1)(2x-3), 其中x= . 答案: 解:原式=(3x-1)(2x-3)[(3x-1)-(2x-3)-x] =(3x-1)(2x-3)×2 =2(3x-1)(2x-3). 当x=时,原式=2×(3× -1)×(2× -3)=- . |
课堂小结 | 这节课你有哪些收获?你认为自己的表现如何? 提公因式分解因式,公因式可能为多项式。当公因式相同时,可以直接提取公因式,当公因式互为相反数时,应先变形,使之相同,再提取。
|
湘教版七年级下册3.2 提公因式法优质习题ppt课件: 这是一份湘教版七年级下册3.2 提公因式法优质习题ppt课件,文件包含第2课时公因式为多项式的提公因式法课件pptx、第1课时公因式为单项式的提公因式法课件pptx、32提公因式法练习pptx、第1课时公因式为单项式的提公因式法教案doc、第2课时公因式为多项式的提公因式法教案doc等5份课件配套教学资源,其中PPT共28页, 欢迎下载使用。
数学七年级下册3.2 提公因式法优秀习题ppt课件: 这是一份数学七年级下册3.2 提公因式法优秀习题ppt课件,文件包含第2课时公因式为多项式的提公因式法课件pptx、第1课时公因式为单项式的提公因式法课件pptx、32提公因式法练习pptx、第1课时公因式为单项式的提公因式法教案doc、第2课时公因式为多项式的提公因式法教案doc等5份课件配套教学资源,其中PPT共28页, 欢迎下载使用。
湘教版3.2 提公因式法精品ppt课件: 这是一份湘教版3.2 提公因式法精品ppt课件,文件包含教学课件七下·湘教32提公因式法第2课时pptx、32提公因式法第2课时同步练习docx、32提公因式法第2课时教案docx等3份课件配套教学资源,其中PPT共16页, 欢迎下载使用。













