




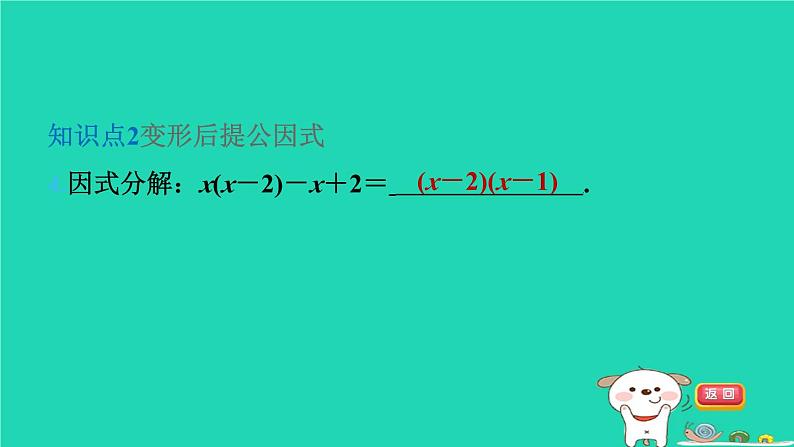

还剩7页未读,
继续阅读
2024七年级数学下册第3章因式分解3.2提公因式法第2课时变形后提公因式法习题课件新版湘教版
展开
这是一份2024七年级数学下册第3章因式分解3.2提公因式法第2课时变形后提公因式法习题课件新版湘教版,共14页。
提公因式法3.2第2课时 变形后提公因式法构造已知条件中的式子求值:求值问题中当利用已知条 件不容易解出每个字母的值时,可先通过提公因式将待求式 进行转化,然后运用整体代入法求出式子的值.名师点金知识点1变形后确定公因式1.(母题:教材P60说一说)多项式4a2b(a-b)-6ab2(b-a)中, 各项的公因式是( D )D2.观察下列各组式子:①2a+b和a+b; ②5m(a-b)和-a+b;③3(a+b)和-a-b; ④x2-y2和x2+y2.其中有公因式的是( B )B3.(x+y-z)(x-y+z)与(y+z-x)(z-x-y)的公因式是( A )A知识点2变形后提公因式4.因式分解:x(x-2)-x+2= .(x-2)(x-1) 5.多项式(x+2)(2x-1)-x-2可以因式分解成2(x+m)(x+ n),则m-n的值是( C )C6.[2023·湖南师大附中模拟]若m-n=-1,则(m-n)2-2m +2n的值是( A )A易错点 分解因式时易忽视符号变化而出错7.把-a(x-y)-b(y-x)+c(x-y)因式分解,正确的结果是( B )本题易错之处在于提取公因式后没有注意符号变化.B【点拨】 利用分组后提公因式法因式分解8. [新考法 分组分解法]阅读下面因式分解的过程:把多项式am+an+bm+bn因式分解.解法一:am+an+bm+bn=(am+an)+(bm+bn)=a(m+ n)+b(m+n)=(m+n)(a+b);解法二:am+an+bm+bn=(am+bm)+(an+bn)=m(a+ b)+n(a+b)=(a+b)(m+n).请你选择一种方法把下列多项式因式分解:(1)mx-my+nx-ny; (2)2a+4b-3ma-6mb.【解】(方法不唯一)mx-my+nx-ny=(mx-my)+(nx- ny)=m(x-y)+n(x-y)=(x-y)(m+n).2a+4b-3ma-6mb=(2a-3ma)+(4b-6mb)=a(2-3m) +2b(2-3m)=(2-3m)(a+2b). 利用提公因式法探究因式分解的规律9.[新考法 连续分组法]先阅读下列分解因式的过程,再回答 所提出的问题:1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]=(1+x)2(1+x)=(1+x)3.(1)上述因式分解的方法是 ,共应用 了 次;提公因式法 2 (2)若因式分解1+x+x(x+1)+x(x+1)2+…+x(x+1)2 024, 则需应用上述方法 次,结果是 ;(3)因式分解:1+x+x(x+1)+x(x+1)2+…+x(x+1)n(n为正 整数).【解】原式=(1+x)n+1.2024 (1+x)2025
提公因式法3.2第2课时 变形后提公因式法构造已知条件中的式子求值:求值问题中当利用已知条 件不容易解出每个字母的值时,可先通过提公因式将待求式 进行转化,然后运用整体代入法求出式子的值.名师点金知识点1变形后确定公因式1.(母题:教材P60说一说)多项式4a2b(a-b)-6ab2(b-a)中, 各项的公因式是( D )D2.观察下列各组式子:①2a+b和a+b; ②5m(a-b)和-a+b;③3(a+b)和-a-b; ④x2-y2和x2+y2.其中有公因式的是( B )B3.(x+y-z)(x-y+z)与(y+z-x)(z-x-y)的公因式是( A )A知识点2变形后提公因式4.因式分解:x(x-2)-x+2= .(x-2)(x-1) 5.多项式(x+2)(2x-1)-x-2可以因式分解成2(x+m)(x+ n),则m-n的值是( C )C6.[2023·湖南师大附中模拟]若m-n=-1,则(m-n)2-2m +2n的值是( A )A易错点 分解因式时易忽视符号变化而出错7.把-a(x-y)-b(y-x)+c(x-y)因式分解,正确的结果是( B )本题易错之处在于提取公因式后没有注意符号变化.B【点拨】 利用分组后提公因式法因式分解8. [新考法 分组分解法]阅读下面因式分解的过程:把多项式am+an+bm+bn因式分解.解法一:am+an+bm+bn=(am+an)+(bm+bn)=a(m+ n)+b(m+n)=(m+n)(a+b);解法二:am+an+bm+bn=(am+bm)+(an+bn)=m(a+ b)+n(a+b)=(a+b)(m+n).请你选择一种方法把下列多项式因式分解:(1)mx-my+nx-ny; (2)2a+4b-3ma-6mb.【解】(方法不唯一)mx-my+nx-ny=(mx-my)+(nx- ny)=m(x-y)+n(x-y)=(x-y)(m+n).2a+4b-3ma-6mb=(2a-3ma)+(4b-6mb)=a(2-3m) +2b(2-3m)=(2-3m)(a+2b). 利用提公因式法探究因式分解的规律9.[新考法 连续分组法]先阅读下列分解因式的过程,再回答 所提出的问题:1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]=(1+x)2(1+x)=(1+x)3.(1)上述因式分解的方法是 ,共应用 了 次;提公因式法 2 (2)若因式分解1+x+x(x+1)+x(x+1)2+…+x(x+1)2 024, 则需应用上述方法 次,结果是 ;(3)因式分解:1+x+x(x+1)+x(x+1)2+…+x(x+1)n(n为正 整数).【解】原式=(1+x)n+1.2024 (1+x)2025
相关资料
更多









