初中人教版第十二章 全等三角形综合与测试当堂检测题
展开
这是一份初中人教版第十二章 全等三角形综合与测试当堂检测题,共9页。试卷主要包含了根据下列证明过程填空,填空等内容,欢迎下载使用。
第12章《全等三角形》 单元考点分类训练一.全等三角形的性质1.如图,D是BC上一点,AB=AD,BC=DE.△ABC≌△ADE,求证:∠CDE=∠BAD. 2.如图,△ADB≌△EDB,△BDE≌△CDE.B、E、C在一条直线上.(1)BD是∠ABE的平分线吗?为什么?(2)DE⊥BC吗?为什么?(3)点E平分线段BC吗?为什么? 3.如图,已知△ABC≌△ADE,BC的边长线交AD于F,交AE于G,∠ACB=105°,∠CAD=10°,∠ADE=25°,求∠DFB和∠AGB的度数. 4.根据下列证明过程填空:(1)如图1,已知直线EF与AB、CD都相交,且AB∥CD,试说明∠1=∠2的理由.解:∵AB∥CD (已知)∴∠2=∠3( )∵∠1=∠3( )∴∠1=∠2( 等量代换 )(2)如图2,已知:△AOC≌△BOD,试说明AC∥BD成立的理由.解:∵△AOC≌△BOD∴∠A= ( )∴AC∥BD ( ) 5.如图,已知△ABF≌△ACF≌△DBF,∠FAB:∠ABF:∠AFB=4:7:25.(1)求△ABF各内角的度数;(2)延长AF交BD于点G,求证:AG是△ABC的高;(3)求∠CFD的度数;(4)求∠AED的度数. 二.全等三角形的判定与性质6.如图,点P为∠AOB的角平分线OC上的一点,过点P作PM∥OB交OA于点M,过点P作PN⊥OB于点N.当∠AOB=60°时,求∠OPN的度数.(1)依题意,补全图形;(2)完成下面的解题过程.解:∵PN⊥OB于点N,∴∠PNB= °( )(填推理的依据).∵PM∥OB,∴∠MPN=∠PNB=90°,∠POB= ( )(填推理的依据).∵OP平分∠AOB,且∠AOB=60°,∴∠POB=∠AOB=30°(角的平分线的定义).∴∠MPO= °.∵∠MPO+∠OPN=∠MPN,∴∠OPN= °. 7.在△ABC中,D为AC的中点,DM⊥AB于M,DN⊥BC于N,且DM=DN.(Ⅰ)求证:△ADM≌△CDN.(Ⅱ)若AM=2,AB=AC,求四边形DMBN的周长. 8.填空:(将下面的推理过程及依据补充完整)已知:△ABC的高AD所在直线与高BE所在直线相交于点F,过点F作FG∥BC,交直线AB于点G.如图,若△ABC为锐角三角形,且∠ABC=45°.求证:①△BDF≌△ADC;②FG+DC=AD;①证明:∵AD,BE为高.∴∠ADB=∠BEC=90°.∵∠ABC=45°,∴∠BAD=∠ =45°.∴AD= .∵∠BEC=90°,∴∠CBE+∠C=90°( ).又∵∠DAC+∠C=90°,∴∠CBE=∠DAC( ).在△FDB和△CDA中,.∴△FDB≌△CDA( ).②∵△FDB≌△CDA,∴DF=DC( ).∵GF∥BC,∴∠AGF=∠ABC=45°( ).∴∠AGF=∠ .∴FA=FG.∴FG+DC=FA+DF=AD.9.如图,在△ABC中,AC=BC,点D在AB边上,点E在BC边上,连接CD,DE.已知∠ACD=∠BDE,CD=DE.(1)猜想AC与BD的数量关系,并证明你的猜想;(2)若AD=3,BD=5,求CE的长. 10.如图,已知凸五边形ABCDE中,EC,EB为其对角线,EA=ED.(1)如图1,若∠A=60°,∠CDE=120°,且CD+AB=BC.求证:EC平分∠BCD;(2)如图2,∠A与∠D互补,∠DEA=2∠CEB,若凸五边形ABCDE面积为30,且CD=AB=4.求点E到BC的距离. 11.如图,△AOC和△BOD中,OA=OC,OB=OD,∠AOC=∠BOD=α(0<α<90°),AD与BC交于点P.(1)求证:△AOD≌△COB;(2)求∠APC(用含α的式子表示);(3)过点O分别作OM⊥AD,ON⊥BC,垂足分别为点M、N,请直接写出OM和ON的数量关系. 三.角平分线的性质12.如图,在△ABC中,∠C=90°,CD=1.8,BD=3.(1)若∠2=∠B,求AC的长.(2)若∠1=∠2,求AC的长. 13.△ABC(∠C>90°)的三条角平分线相交于点D,延长AD交BC于点E.作AF⊥BC,交BC延长线于点F.(1)若∠BAC=40°,则∠BDC= °;(2)判断∠CDE与∠ABD的数量关系,并说明理由;(3)求证∠ACD=∠EAF+∠ABD. 14.如图,在△ABC中,∠ABC=90°,BD是AC边上的高,AE是∠BAC的角平分线,分别交BD、BC于点G、E,过点B作AE的垂线BF,分别交AE、AC于点H、F.(1)求证:BF平分∠DBC;(2)若∠ABF=3∠C,求∠C的度数. 15.已知直线EF与直线AB、CD分别交于E、F两点,∠AEF和∠CFE的角平分线交于点P,且∠AEP+∠CFP=90°.(1)求证:AB∥CD;(2)如图2,∠PEF和∠PFM的角平分线交于点Q,求∠Q的度数;(3)如图3,若∠AEP:∠CFP=2:1,延长线段EP得射线EP1,延长线段FP得射线FP2,射线EP1绕点E以每秒15°的速度逆时针旋转360°后停止,射线FP2绕点F以每秒3°的速度顺时针旋转180°以后停止.设它们同时旋转t秒,问t为多少时,射线EP1∥FP2,直接写出t的值t= 秒.16.在△ABC中,AC=BC,∠C=90°,点D是线段BC上一点,以AD为腰在AD右边作等腰△ADE,AD=AE.(1)如图1,若AD平分∠BAC,且CD=1,求AB的长度.(2)如图2,当∠EDC=∠BAD,连接BE交AC于点F,求证:BD=2CF 17.知识储备:(1)如图1,AD是△ABC的高,则△ABC的面积S△ABC=BC•AD.比例的性质:若,则.知识运用:(2)如图2,BE是△ABC的角平分线,运用上述知识,求证:;知识延展:(3)如图3,△ABC的角平分线BE平分△ABC的周长,求证:△ABC是等腰三角形.
相关试卷
这是一份初中数学人教版八年级上册12.1 全等三角形练习,共10页。试卷主要包含了填空题,选择题,解答题等内容,欢迎下载使用。
这是一份2021学年12.2 三角形全等的判定课后测评,共8页。试卷主要包含了已知等内容,欢迎下载使用。
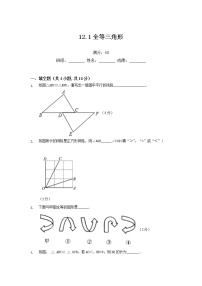
这是一份2021学年第十二章 全等三角形综合与测试随堂练习题,共4页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。