






- 4.3.1 公式法 第一课时 课件 课件 17 次下载
- 4.3.1 公式法(一) 第一课时 教学设计 教案 12 次下载
- 4.3.2 公式法(二) 第二课时 教学设计 教案 12 次下载
- 5.1.1 认识分式 第一课时 课件 课件 16 次下载
- 5.1.1 认识分式 第一课时 教学设计 教案 11 次下载
初中数学北师大版八年级下册第四章 因式分解3 公式法评优课课件ppt
展开(1)提取公因式法:ma+mb+mc=m(a+b+c)(2)运用公式法: ① a2-b2=(a+b)(a-b)
2、把下列各式分解因式
①ax4-ax2 ② x4-16
解:原式=ax2(x2-1) =ax2(x+1)(x-1)
解:原式=(x2+4)(x2-4) =(x2 +4)(x+2)(x-2)
1、分解因式学了哪些方法?
(有公因式,先提公因式)
1、分解因式x2-25能用平方差公式进行因式分解的多项式有什么特点?
2、下面的多项式能用平方差公式分解因式吗?(1) x2+2xy+y2 (2) 9a2-6ab+b2
(1)符号相反的两项 (2)平方差
活动探究:观察与思考,回答下面两个问题。(小组讨论,3min)
3.除了平方差公式外,还学过了哪些公式?
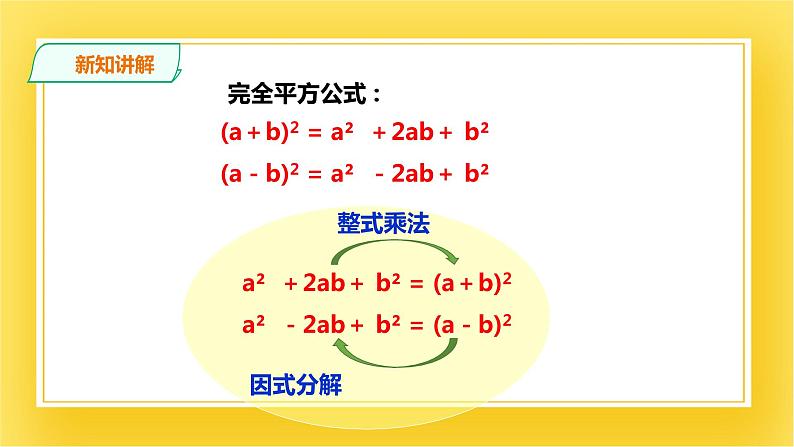
a² +2ab+ b² = (a+b)2 a² -2ab+ b² = (a-b)2
(a+b)2 = a² +2ab+ b²(a-b)2 = a² -2ab+ b²
2、有两个“项”的平方
3、有这两“项”的2倍或-2倍
“头” 平方, “尾” 平方, “头” “尾”两倍中间放.
(1)x2+14x+49
例3.把下列完全平方式因式分解
a² +2 a b+b² =(a+b)2
总结:正确找出a² +2 a b+b² =(a+b)2 式子中的a和b。
解:原式=x2+2·x·7+72 =(x+7)2
(2)(m+n)2-6( m+n )+9
解:原式= (m+n)2-2·( m+n )·3+32 =[(m+n)-3] 2 = (m+n-3)2
总结: a²+2ab+b² =(a+b)2 式子中的a和b既可以是一个单项式的形式,也可以是一个多项式的形式。
例4.把下列各式因式分解
(1)3ax2+6axy+3ay2 (2) -x2-4y2+4xy
解:原式=-(x2+4y2-4xy ) =-(x2-4xy+4y2 ) =-[x2-2·x·2y +(2y)2] = -(x-2y)2
解:原式=3a(x2 +2xy +y2) = 3a (x+y) 2
总结:注意观察多项式的形式,通过变形提取负号,提负号括号里每一项都要变号。因式分解一定要分解彻底。
变式1:分解因式:(1) 16x2-24x+9
解:(1)16x2-24x+9 =(4x)2-2·4x·3+32 =(4x-3)2
变式2: 分解因式: (1) 3ax2-6axy+3ay2 (2) (a+b)2-18(a+b)+81
解:(1)3ax2-6axy+3ay2=3a(x2-2xy+y2)=3a(x-y)2
(2)(a+b)2-18(a+b)+81=(a+b)2-2·(a+b)·9+92=(a+b-9)2
(1)-a3b3+2a2b3-ab3
解:原式=-ab3(a2-2a×1+12) =-ab3(a-1)2
(2)9 - 12(a-b) + 4 (a-b)2
解:原式=32-2×3×2(a-b)+[2(a-b)] 2 = [3-2(a-b)] 2 =(3-2a+2b)2
已知x2+4x+y2-2y+5=0,求 xy 的值。
解:由x2+4x+y2-2y+5=(x2+4x+4)+(y2-2y+1) =(x+2)2+(y-1)2=0得 x+2=0,y-1=0 ∴x=-2,y=1 ∴ xy =-2×1=-2
因式分解一提 ① 对任意多项式分解因式,都必须首先考虑提取公 因式。二套 ② 对于二项式,考虑应用平方差公式分解。 对于 三项式,考虑应用完全平方公式 。三查 ③检查:特别看看多项式因式是否分解彻底。
4.3.2 公式法a² +2 ab+b² =(a+b)2 例题练习
1、分解因式(1)x2+12xy+36y2 (2)32a4+48a2b2+18b4 (3)-2xy-x2-y2 (4)12-36(x-y)+27(x-y)2
初中数学北师大版八年级下册3 公式法课文配套ppt课件: 这是一份初中数学北师大版八年级下册<a href="/sx/tb_c15839_t3/?tag_id=26" target="_blank">3 公式法课文配套ppt课件</a>,共20页。PPT课件主要包含了学习目标,平方差公式分解因式,回忆完全平方公式,回顾与思考,完全平方公式,完全平方式的特点,变式训练等内容,欢迎下载使用。
北师大版八年级下册第四章 因式分解3 公式法优秀ppt课件: 这是一份北师大版八年级下册第四章 因式分解3 公式法优秀ppt课件,共20页。PPT课件主要包含了把下列各式分解因式,有公因先提公因式,因式分解要彻底,典例赏析,知识点二,都是有3项,从每一项看,从符号看,从项数看,熟知公式特征等内容,欢迎下载使用。
北师大版八年级下册第四章 因式分解3 公式法习题ppt课件: 这是一份北师大版八年级下册第四章 因式分解3 公式法习题ppt课件,共15页。PPT课件主要包含了3x+12,答案呈现,②④⑤,x4答案不唯一等内容,欢迎下载使用。














