- 4.3.1 公式法(一) 第一课时 教学设计 教案 12 次下载
- 4.3.2 公式法 第二课时 课件 课件 15 次下载
- 5.1.1 认识分式 第一课时 课件 课件 16 次下载
- 5.1.1 认识分式 第一课时 教学设计 教案 11 次下载
- 5.1.2 认识分式 第二课时 课件 课件 16 次下载
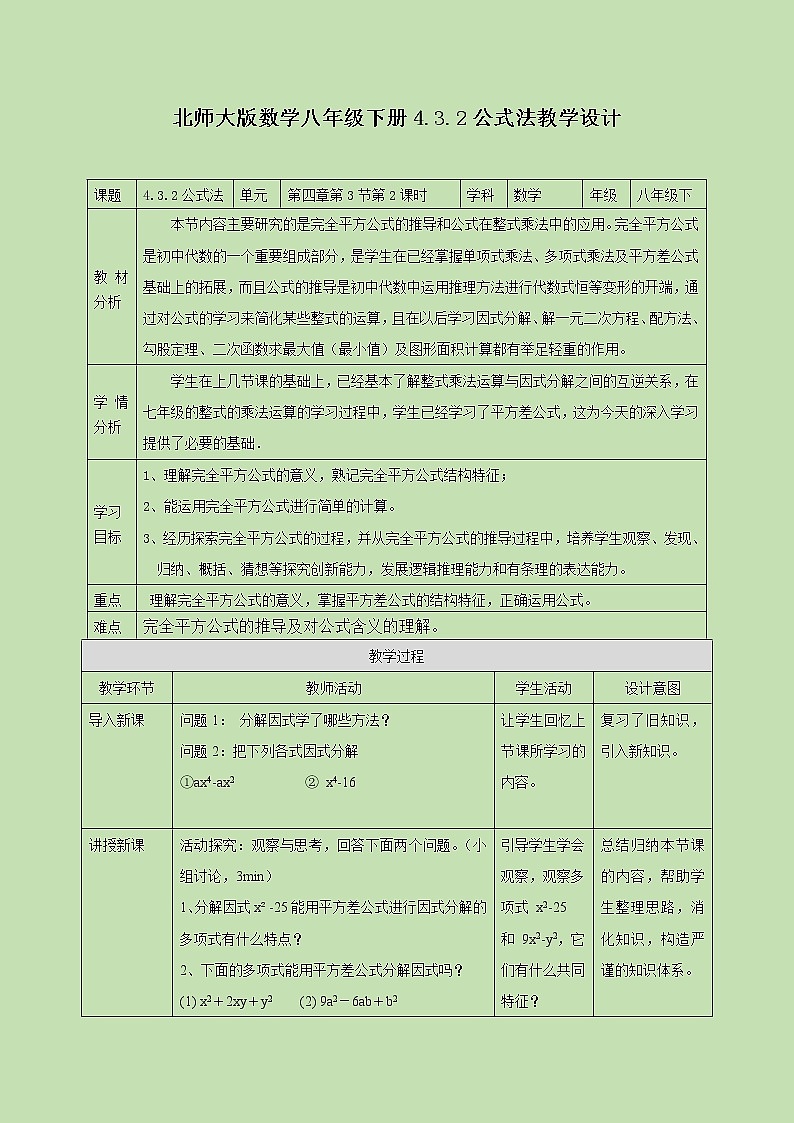
初中数学北师大版八年级下册第四章 因式分解3 公式法精品第二课时教学设计及反思
展开课题
4.3.2公式法
单元
第四章第3节第2课时
学科
数学
年级
八年级下
教材分析
本节内容主要研究的是完全平方公式的推导和公式在整式乘法中的应用。完全平方公式是初中代数的一个重要组成部分,是学生在已经掌握单项式乘法、多项式乘法及平方差公式基础上的拓展,而且公式的推导是初中代数中运用推理方法进行代数式恒等变形的开端,通过对公式的学习来简化某些整式的运算,且在以后学习因式分解、解一元二次方程、配方法、勾股定理、二次函数求最大值(最小值)及图形面积计算都有举足轻重的作用。
学情分析
学生在上几节课的基础上,已经基本了解整式乘法运算与因式分解之间的互逆关系,在七年级的整式的乘法运算的学习过程中,学生已经学习了平方差公式,这为今天的深入学习提供了必要的基础.
学习
目标
1、理解完全平方公式的意义,熟记完全平方公式结构特征;
2、能运用完全平方公式进行简单的计算。
3、经历探索完全平方公式的过程,并从完全平方公式的推导过程中,培养学生观察、发现、归纳、概括、猜想等探究创新能力,发展逻辑推理能力和有条理的表达能力。
重点
理解完全平方公式的意义,掌握平方差公式的结构特征,正确运用公式。
难点
完全平方公式的推导及对公式含义的理解。
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
问题1: 分解因式学了哪些方法?
问题2:把下列各式因式分解
①ax4-ax2 ② x4-16
让学生回忆上节课所学习的内容。
复习了旧知识,引入新知识。
讲授新课
活动探究:观察与思考,回答下面两个问题。(小组讨论,3min)
1、分解因式x² -25能用平方差公式进行因式分解的多项式有什么特点?
2、下面的多项式能用平方差公式分解因式吗?
(1) x2+2xy+y2 (2) 9a2-6ab+b2
什么是完全平方公式?
(a+b)2= a2+2ab+b2
(a-b)2 = a2-2ab+b2
因式分解 :
a2+2ab+b2= (a+b)2
a2-2ab+b2= (a-b)2
完全平方式的特点:
1、必须是三项式
2、有两个“项”的平方
3、有这两“项”的2倍或-2倍
口诀:“头” 平方, “尾” 平方, “头” “尾”两倍中间放。
例3.把下列完全平方式因式分解
变式3:
(1)-a3b3+2a2b3-ab3
(2)9 - 12(a-b) + 4 (a-b)2
拓展提高:
已知x2+4x+y2-2y+5=0,求 xy 的值。
作业布置:
1、分解因式
(1)x2+12xy+36y2 (2)32a4+48a2b2+18b4
(3)-2xy-x2-y2 (4)12-36(x-y)+27(x-y)2
2、如果x2+mxy+16y2是一个完全平方式,那么m的值为( )
A、6 B、±6 C、8 D、±8
引导学生学会观察,观察多项式 x2-25 和 9x2-y2,它们有什么共同特征?
独立完成,提问学生回答,总结出公式法的要点和易错点。
小组讨论,时间3min,总结出完全平方式的特点。
自己总结口诀
总结归纳本节课的内容,帮助学生整理思路,消化知识,构造严谨的知识体系。
学生通过观察、对比,把整式乘法中的平方差公式进行逆向运用,发展学生的观察能力与逆向思维能力。
让学生积极参与数学再创造活动,化特殊为一般,培养数学建模思想,化归思想。
鼓励学生用自己的语言表述,从而提高学生的语言组织与表达能力。为此结合两个公式的特征,可用顺口溜强化记忆。
课堂小结
因式分解
提问学生自己总结。
总结归纳本节课的内容,帮助学生整理思路,消化知识,构造严谨的知识体系。
板书
4.3.2 公式法(二)
a2 +2 ab+b2 =(a+b)2
a2 -2 ab+b2 = (a - b)2
例题
变式
北师大版八年级下册3 公式法第二课时教案设计: 这是一份北师大版八年级下册3 公式法第二课时教案设计,共3页。
北师大版八年级下册第四章 因式分解3 公式法第一课时教学设计: 这是一份北师大版八年级下册第四章 因式分解3 公式法第一课时教学设计,共3页。
八年级数学教学设计:运用公式法: 这是一份八年级数学教学设计:运用公式法,共7页。教案主要包含了复习,新课,课堂练习,小结,作业等内容,欢迎下载使用。