北师大版七年级下册3 探索三角形全等的条件图文课件ppt

这是一份北师大版七年级下册3 探索三角形全等的条件图文课件ppt，共18页。PPT课件主要包含了边边边公理，三角形的稳定性等内容，欢迎下载使用。
根据定义判定两个三角形全等，需要知道哪些条件?
三条边对应相等，三个角对应相等.
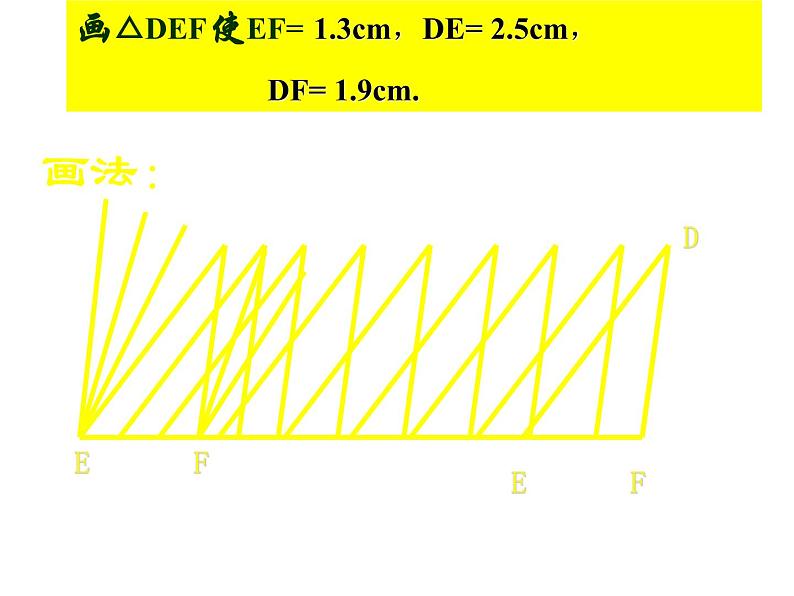
请按照下面的方法，用刻度尺和圆规画△DEF,使其三边分别为1.3cm，1.9cm和2.5cm.画法：1、画线段EF= 1.3cm.2、分别以E，F为圆心， 2.5cm ， 1.9cm长为 半径画两条圆弧，交于点D3、连结DE，DF. △DEF就是所求的三角形.
把你画的三角形与其他同学所画的三角形进行比较，它们能互相重合吗？
画△DEF使EF= 1.3cm，DE= 2.5cm， DF= 1.9cm.
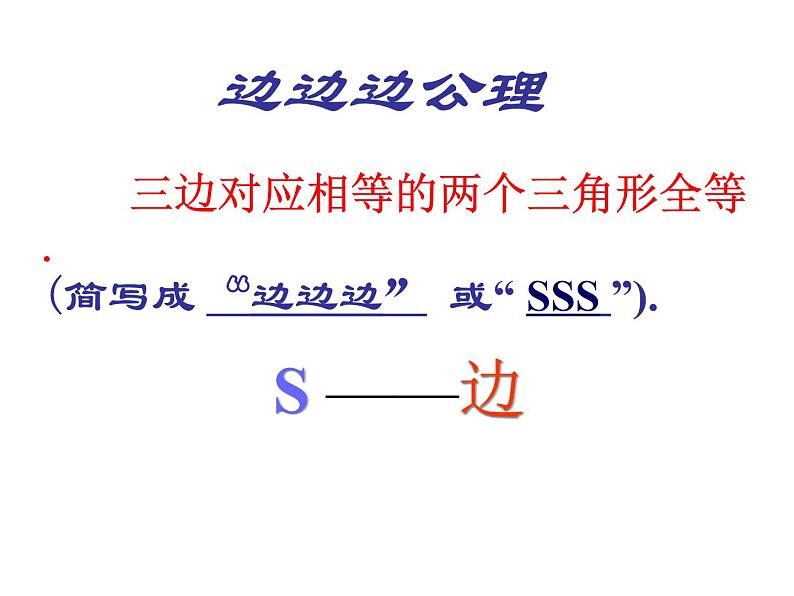
三边对应相等的两个三角形全等.(简写成 “边边边” 或“ SSS ”).
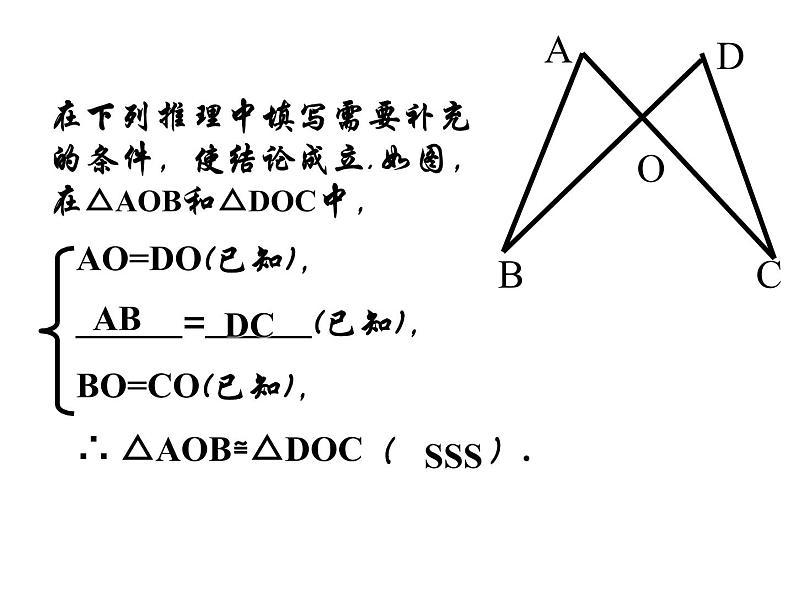
在下列推理中填写需要补充的条件，使结论成立.如图，在△AOB和△DOC中，
AO=DO(已知)，______=______(已知)，BO=CO(已知)，∴ △AOB≌△DOC（ ）.
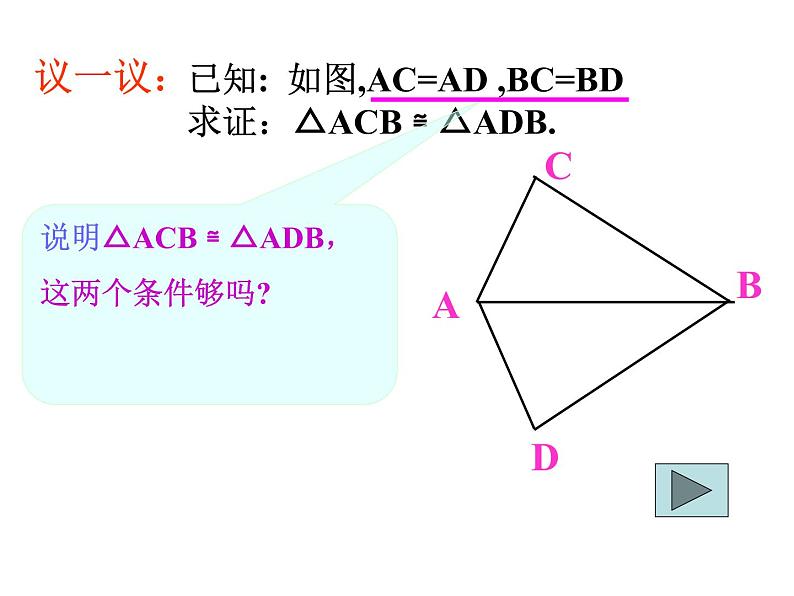
已知: 如图,AC=AD ,BC=BD 求证：△ACB ≌ △ADB.
说明△ACB ≌ △ADB，这两个条件够吗?
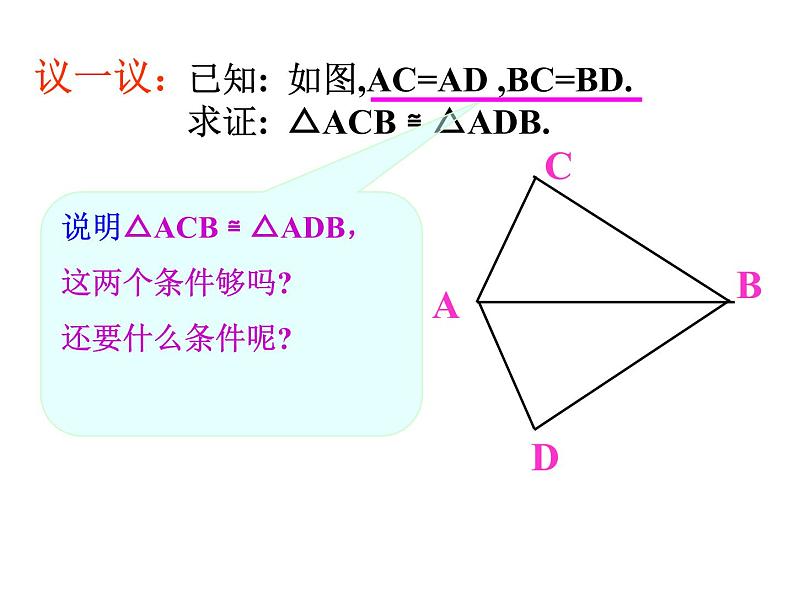
已知: 如图,AC=AD ,BC=BD. 求证: △ACB ≌ △ADB.
说明△ACB ≌ △ADB，这两个条件够吗?还要什么条件呢?
已知: 如图，AC=AD，BC=BD. 求证: △ACB ≌ △ADB.
它既是△ACB的一条边,
又是△ADB的一条边，
△ACB 和△ADB的公共边.
例1 如图，在四边形ABCD中，AB=CD，AD=CB，则∠A= ∠C.请说明理由.
解 在△ABD和△CDB中,
AB=CD （已知）,
AD=CB （已知）,
∴ △ABD≌△CDB
∴ ∠A= ∠C( ）.
全等三角形的对应角相等
在△ACB 和 △ADB中，
AC= AD（已知）， BC= BD（已知）， AB= AB (公共边），
当三角形的三条边长确定时，三角形的形状、大小完全被确定，这个性质叫三角形的稳定性.四边形不具有稳定性.
三角形的稳定性在生活中的应用：
例2 已知∠BAC（如图），用直尺和圆规作∠BAC的平分线AD，并说出该作法正确的理由.
1.边边边公理：三边对应相等的两个三角形全等（简写成“边边边”或“SSS”）.
2.边边边公理的发现过程所用到的数学方法（包括画 图、猜想、分析、归纳等).
3.边边边公理的应用中所用到的数学方法: 证明线段（或角相等） 证明线段（或角）所在的两个三角形全等.
1. 说明两个三角形全等所需的条件应按对应边的顺序书写.2. 结论中所出现的边必须在所证明的两个三角形中.
用结论说明两个三角形全等需注意：