2021学年1 认识三角形课时作业

5.1 认识三角形(2) 同步练习

本课导学

点击要点

    三角形内角和等于________．

学习策略

    解决本节习题主要应用三角形内角和定理．

中考展望

    本节知识应用广泛，单独考查时多为填空、选择题

随堂测评

基础巩固

一、训练平台（每小题4分，共40分）

1．一个三角形的三个内角分别为α，α-1，α+1（α>1°），则这个三角形三个内角的度数分别为（  ）

    A．44°，45°，91°     B．49°，59°，69°

    C．59°，60°，61°     D．30°，60°，90°

2．给定下列条件，不能判定三角形是直角三角形的是（  ）

    A．∠A+∠B=∠C      B．∠A：∠B：∠C=1：2：3

    C．2∠A=3∠B=4∠C   D．∠A-∠B=∠C

3．如图1所示，已知AB⊥BD，AC⊥CD，∠A=35°，则∠D的度数为（  ）

A．35°     B．65°     C．55°     D．45°

       (1)               (2)              (3)               (4)

4．如图2所示，AB∥CD，∠A=55°，∠C=80°，则∠M等于（  ）

A．55°     B．25°     C．35°     D．15°

5．在△ABC中，若∠A=78°36′，∠B=57°36°，则∠C=_______．

6．已知在Rt△ABC中，∠C=90°，∠BAC=30°，AB=10，那么BC=_______．

7．如图3所示，将一幅直角三角板叠在一起，使直角顶点重合于点O，使∠AOB+∠DOC=_______．

8．在一个三角形中，最多有______个锐角，有______个直角，有_______个钝角．

9．在直角三角形中，有一个锐角是另一个锐角2倍，则这两个锐角的度数是_________．

10．在△ABC中，∠A：∠B=5：7，∠C-∠A=10°，则∠C=________．

能力升级

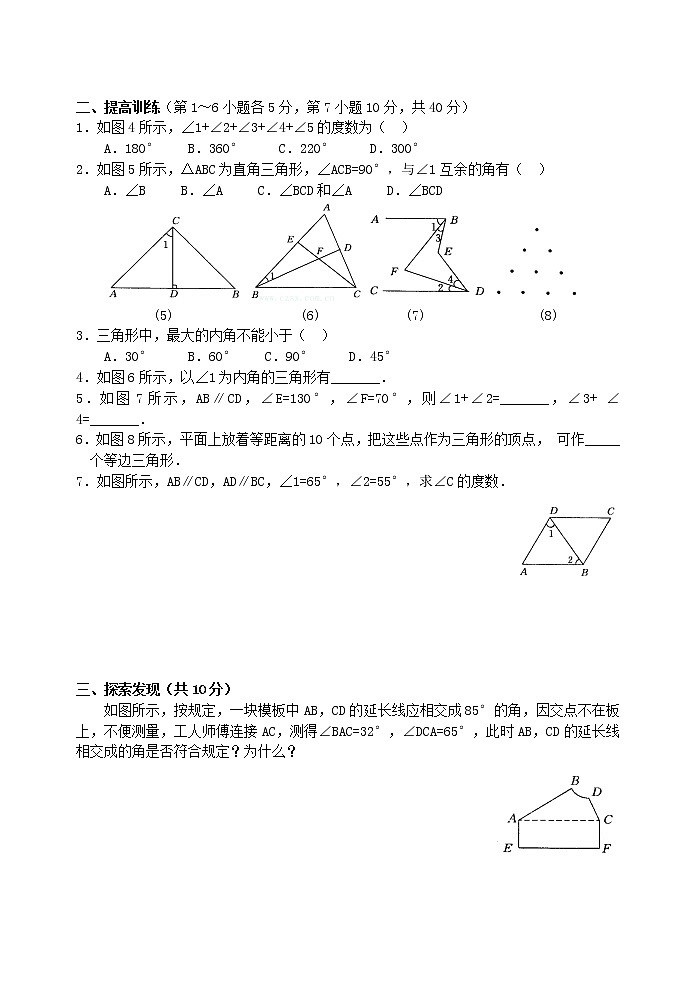
二、提高训练（第1～6小题各5分，第7小题10分，共40分）

1．如图4所示，∠1+∠2+∠3+∠4+∠5的度数为（  ）

A．180°    B．360°     C．220°     D．300°

2．如图5所示，△ABC为直角三角形，∠ACB=90°，与∠1互余的角有（  ）

A．∠B     B．∠A     C．∠BCD和∠A     D．∠BCD

       (5)                  (6)            (7)                (8)

3．三角形中，最大的内角不能小于（  ）

    A．30°     B．60°    C．90°     D．45°

4．如图6所示，以∠1为内角的三角形有_______．

5．如图7所示，AB∥CD，∠E=130°，∠F=70°，则∠1+∠2=_______，∠3+∠4=_______．

6．如图8所示，平面上放着等距离的10个点，把这些点作为三角形的顶点，可作_____个等边三角形．

7．如图所示，AB∥CD，AD∥BC，∠1=65°，∠2=55°，求∠C的度数．

三、探索发现（共10分）

如图所示，按规定，一块模板中AB，CD的延长线应相交成85°的角，因交点不在板上，不便测量，工人师傅连接AC，测得∠BAC=32°，∠DCA=65°，此时AB，CD的延长线相交成的角是否符合规定？为什么？

四、拓展创新（共10分）

    如图所示，AB⊥BC，DC⊥BC，若∠DBC=45°，∠A=70°，求∠D，∠AED，∠BFE的度数．

中考演练

（中考预测题）已知△ABC有两条边长分别为2和7，另一边长是关于x的方程2x-1=4x-k+3的解，求k的取值范围．

答案:

本课导学

    180°

随堂测评

一、1．C  2．C  3．A  4．B  5．43°48′ 

6．5  7．180°  8．3  1  1

 9．30°，60°  10．60°

二、1．A  2．C  3．B  4．△BEF，△ABD 

5．70°，60°  6．15

7．解：因为AB∥CD，AD∥BC，

所以∠BDC=∠2=55°，∠DBC=∠1=65°，

所以∠C=180°-∠BDC-∠DBC=60°．

三、不符合，因为三角形内角和应等于180°．

四、45°，70°，115°

中考演练

因为x=，由三角形三边关系得出5<<9，

所以14<k<22．