北师大版数学七年级下册 4.1.3《认识三角形》第3课时 课件+分层练习（含答案解析）

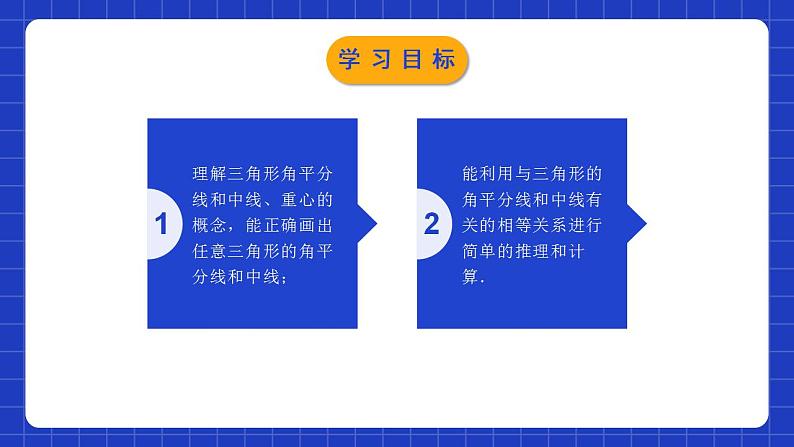
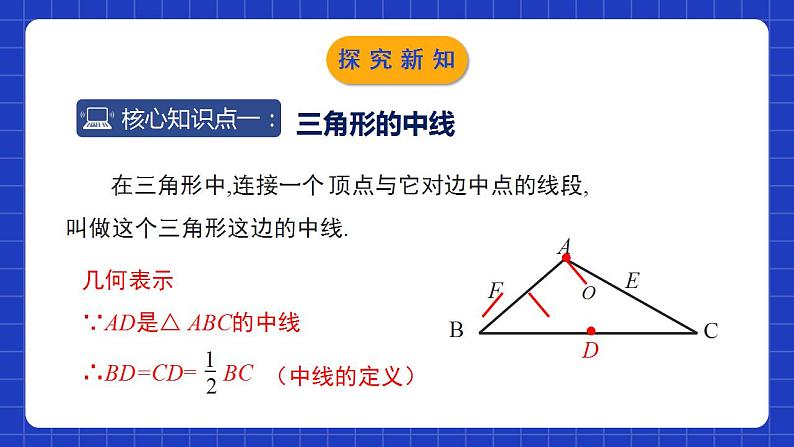
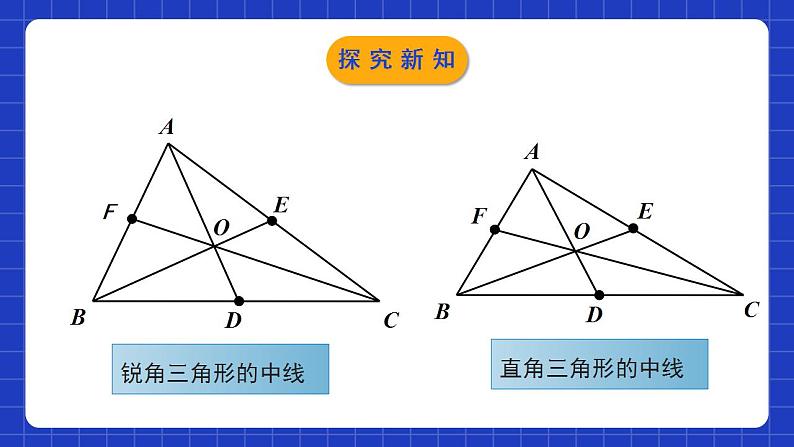
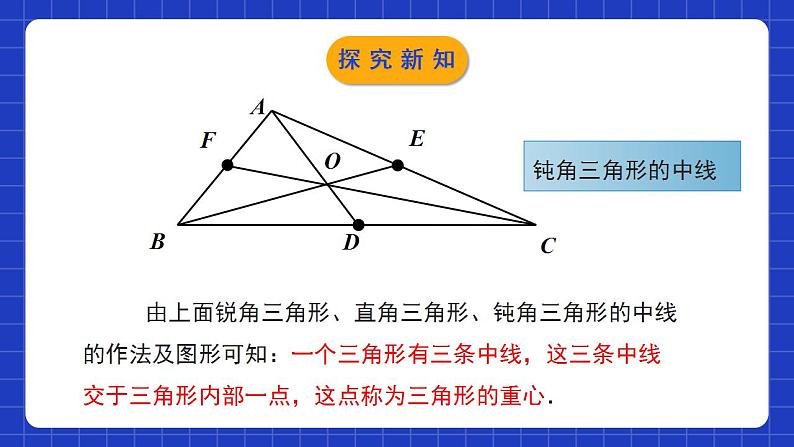
4.1.3认识三角形第3课时学习目标1理解三角形角平分线和中线、重心的概念，能正确画出任意三角形的角平分线和中线；2能利用与三角形的角平分线和中线有关的相等关系进行简单的推理和计算．把一条线段分成两条相等的线段的点从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线。或或情境导入 同学们一定看过杂技表演，思考一下杂技演员们为什么能稳稳的进行表演呢？情境导入三角形的中线在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形这边的中线.D几何表示∵AD是△ ABC的中线●●EFO（中线的定义）探究新知议一议：（1）在纸上画出一个锐角三角形，并画出它的三条中线，它们有怎样的位置关系？与同伴进行交流．（2）钝角三角形和直角三角形的三条中线也有同样的位置关系吗？折一折，画一画，并与同伴进行交流．探究新知EOFDCBAEOFDCBA锐角三角形的中线直角三角形的中线探究新知EOFDCBA由上面锐角三角形、直角三角形、钝角三角形的中线的作法及图形可知：一个三角形有三条中线，这三条中线交于三角形内部一点，这点称为三角形的重心．钝角三角形的中线探究新知 生活中，有时你会发现可以你用一个手指能顶起一支笔或一本书，那这是为什么呢？“重心”探究新知例：张大爷的两个儿子都长大成人了，也该分家了．于是张大爷准备把如图所示的一块三角形田地平均分给两个儿子，两个儿子要求分成的两块田地的形状仍然是三角形，请你帮助张大爷提出一种平分的方案．解：作BC边上的中线AD（或AC边上的中线BE或AB边上的中线CF）．分析：三角形的任意一条中线都能把三角形分成面积相等的两部分，即等底同高的两个三角形的面积相等；探究新知三角形的角平分线在三角形中，一个内角的角平分线与它的对边相交，这个角的顶点与交点之间的线段叫做三角形的角平分线．21DCBA几何表示：∵AD是△ABC的角平分线，∴∠1＝∠2= ∠BAC ．探究新知做一做：每人准备锐角三角形、钝角三角形和直角三角形纸片各一个．（1）你能分别画出这三个三角形的三条角平分线吗？（2）你能用折纸的办法得到它们吗？（3）在每个三角形中，这三条角平分线之间有怎样的位置关系？将你的结果与同伴进行交流．探究新知FECDBAFEABDCOO锐角三角形的平分线直角三角形的平分线探究新知FABDCE通过上面三类三角形的角平分线的位置关系，可以发现：一个三角形有三条角平分线，这三条角平分线交于三角形内部一点．这点称为三角形的内心。O注意： 三角形的角平分线是一条线段 , 角的平分线是一条射线.钝角三角形的平分线探究新知解：∵AD是△ABC的角平分线，∠BAC＝68°， ∴∠DAC＝∠BAD＝34°. 在△ABD中，∠B+∠ADB+∠BAD＝180°， ∴∠ADB＝180°－∠B－∠BAD＝110°.例： 如图,在△ABC中,∠BAC=68°，∠B=36°，AD是△ABC的一条角平分线，求∠ADB的度数.探究新知1.下列说法中正确的是(　　)A．三角形的角平分线和中线都是线段B．三角形的角平分线和中线都是射线C．三角形的角平分线是射线，而中线是线段D．三角形的角平分线是线段，而中线是射线A随堂练习2.如图，在△ABC中有四条线段DE，BE，EF，FG，其中有一条线段是△ABC的中线，则该线段是（　　）A．线段DE B．线段BE C．线段EF D．线段FGB随堂练习3．在△ABC中，AD为中线，BE为角平分线，则在以下等式中：①∠BAD=∠CAD；②∠ABE=∠CBE；③BD=DC；④AE=EC．其中正确的是 （　　）A．①② B．③④ C．①④ D．②③D随堂练习4.如图所示，在△ABC中，D，E，F是BC边上的三点，且∠1=∠2=∠3=∠4，AE是哪个三角形的角平分线( ) A.△ABE B.△ADF C.△ABC D.△ABC，△ADFD随堂练习5.如图，已知AD是△ABC的角平分线，CE是△ABC的高，∠BAC＝60°，∠BCE＝40°，求∠ADB的度数．BECDA解：∵AD是△ABC的角平分线，∠BAC＝60°，∴∠DAC＝∠BAD＝30°．∵CE是△ABC的高，∠BCE＝40°，∴∠B＝50°，∴∠ADB＝180°－∠B－∠BAD ＝180°－30°－50°＝100°．随堂练习6.如图,AD是△ABC的角平分线,DE//CA,交AB于点E, DF//BA,交AC于点F.∠1与∠2相等吗?为什么?解:相等.理由:因为AD是△ABC的角平分线,所以∠BAD=∠CAD.因为DE∥CA,所以∠1=∠CAD.因为DF∥BA,所以∠2=∠BAD,所以∠1=∠2.随堂练习7.在△ABC中，AB＝AC，AC边上的中线BD把△ABC的周长分为12 cm和15 cm的两部分，求三角形的各边长．因为中线BD将△ABC的周长分成两部分：(BC＋CD)和(AD＋AB)，谁为12 cm，谁为15 cm，不确定，故应分类讨论；另外题中涉及线段较多，因此可建立方程模型，利用设未知数来求解．分析：随堂练习设AB＝x cm，则AD＝CD＝ x cm.(1)如图①，若AB＋AD＝12 cm，则x＋ x＝12，解得x＝8，即AB＝AC＝8 cm，CD＝4 cm.故BC＝15－4＝11(cm)．此时AB＋AC＞BC，所以三边长分别为8 cm，8 cm，11 cm.解：随堂练习(2)如图②，若AB＋AD＝15 cm，则x＋ x＝15，解得x＝10，即AB＝AC＝10 cm，则CD＝5 cm，故BC＝12－5＝7(cm)．显然此时三角形存在，所以三边长分别为10 cm，10 cm，7 cm.综上所述，此三角形的三边长分别为8 cm，8 cm，11 cm或10 cm，10 cm，7 cm.随堂练习三角形中几条重要线段角平分线：平分内角且与三角形对边相交的线段.中线：连接三角形的顶点与对边中点的线段.平分线段平分面积平分内角课堂小结课程结束