初中数学冀教版七年级下册7.5 平行线的性质练习题

7.5平行线的性质同步练习冀教版初中数学七年级下册

一、选择题（本大题共12小题，共36.0分）

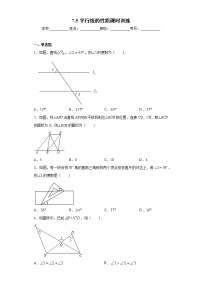
1. 如图，将三角尺与直尺贴在一起，使三角尺的直角顶点在直尺的一边上，若，则的度数等于

A.
B.
C.
D.

2. 如图所示，且，则的度数是

A.
B.
C.
D.

3. 如图，，点E在AC上，若，，则等于

A.
B.
C.
D.

4. 如图，直线，点A在直线上，以点A为圆心，适当长度为半径画弧，分别交直线、于B、C两点，连结AC、若，则的大小为

A.
B.
C.
D.

5. 如图，下列推理错误的是

A. ，
B. ，
C. ，，
D. ，
 

6. 如图，已知直线，点A，B分别在直线a，b上，连结点D是直线a，b之间的一个动点，作交直线b于点C，连结若，则下列选项中不可能取到的度数为

A.  B.  C.  D.

7. 如图，平行线AB、CD被直线AE所截，，则的度数为

A.
B.
C.
D.

8. 如图把一个长方形纸片沿EF折叠后，点D、C分别落在、位置，若，则    

A.
B.
C.
D.

9. 下列说法：不相交的两条直线叫平行线；同位角相等；如果两条直线都和第三条直线平行，那么这两条直线平行；平面内，过一点有且只有一条直线与已知直线垂直；平面内，过一点有且只有一条直线与已知直线平行．正确的个数是

A. 1 B. 2 C. 3 D. 4

10. 将一副三角板按如图所示的位置摆放在直尺上，则的度数为

A.
B.
C.
D.

11. 如图，已知直线，直线c分别与a，b相交，，则的度数为

A.
B.
C.
D.

12. 如图a是长方形纸带，，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的的度数是  

A.  B.  C.  D.

二、填空题（本大题共6小题，共18.0分）

13. 如图，已知直线，，则______．
     

14. 如图，，OE平分，，，，则下列结论：；平分；；其中正确的结论有______填序号

15. 一副直角三角尺叠放如图1所示，现将的三角尺ADE固定不动，将含的三角尺ABC绕顶点A顺时针转动旋转角不超过180度，使两块三角尺至少有一组边互相平行．如图2：当时，则其它所有可能符合条件的度数为______．

16. 如图a是长方形纸带，，将纸带沿EF折叠成图b，则的度数______度，再沿BF折叠成图则图中的的度数是______度．

17. 如图，，，，则______．

18. 如图，ABC的平分线BF与ABC中ACB的相邻外角ACG的平分线CF相交于点F，过F作DF BC，交AB于D，交AC于E，若BDcm，DEcm，求CE的长为____cm．

三、解答题（本大题共7小题，共56.0分）

19. 如图，已知AF分别与BD、CE交于点G、H，，．
    求证：；
    若，探索与的数量关系，并证明你的结论．
    
     

20. 如图，已知，，，，试说明：．
    
    
    
     

21. 光线在不同介质中传播速度不同，从一种介质射向另一种介质时会发生折射．如图，水面AB与水杯下沿CD平行，光线EF从水中射向空气时发生折射，光线变成FH，点G在射线EF上，已知，，求的度数．
    
    
    
    
    
    
     
22. 如图，直线AB、CD相交于点O，且OE为的平分线，，若，求的度数．

23. 完成下面的证明：
    已知：如图，，．
    求证：．
    证明：已知，
    __________________，
    ______，
    已知，
    等量代换，
    __________________，
    ______
    
    
    
    
    
    
     
24. 如图，是等边三角形，点D在AC边上，将绕点C旋转得到．
    求证：．
    若，，求的周长．
     

25. 将一张长方形纸条ABCD按如图所示折叠，若折叠角．
    求的度数；
    求证：是等腰三角形．

答案和解析

1.【答案】D
 

【解析】

【分析】
此题考查了平行线的性质．此题难度不大，注意直角三角形中两锐角互余的应用是解此题的关键．
根据题意得：，即可求得的值，继而求得的度数，然后求得的度数．
【解答】
解：如图，

根据题意得：，
，
，
，
，
．
故选：D．  

2.【答案】B
 

【解析】解：，
，
，
，
故选：B．
根据邻补角的性质可得的度数，然后再根据平行线的性质可得答案．
此题主要考查了平行线的性质，关键是掌握两直线平行，同位角相等．
 

3.【答案】B
 

【解析】解：，
，
，
，
，
．
故选：B．
直接利用平行线的性质得出，进而结合三角形外角的性质得出答案．
此题主要考查了平行线的性质，正确得出度数是解题关键．
 

4.【答案】C
 

【解析】解：点A为圆心，适当长度为半径画弧，分别交直线l1、l2于B、C，
，
，
，
，
，
故选：C．
根据平行线的性质解答即可．
此题考查平行线的性质，关键是根据平行线的性质解答．
 

5.【答案】D
 

【解析】解：，，选项A正确；
，，选项B正确；
，，，选项C正确；
，，选项D错误；
故选：D．
由平行线的判定与性质得出选项A、B、C正确，D错误；即可得出结论．
本题考查了平行线的判定与性质、平行线公理；熟练掌握平行线的判定与性质是解决问题的关键．
 

6.【答案】A
 

【解析】解：延长CD交直线a于E．

，
，
，
，

，
，
故选：A．
延长CD交直线a于由，判断出即可解决问题．
本题考查平行线的判定，三角形的外角等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
 

7.【答案】C
 

【解析】解：，，
，
，
故选：C．
根据平行线的性质和邻补角解答即可．
本题主要考查了平行线的性质，解题时注意：两直线平行，同位角相等．
 

8.【答案】A
 

【解析】

【分析】
本题考查了平行线的性质，翻折变换的性质，熟记性质是解题的关键根据两直线平行，内错角相等可得，再根据翻折变换的性质可得，然后根据平角等于列式计算即可得解 
【解答】
解：如图，长方形纸片对边平行，

 
，
由翻折的性质得，，
．
故选A．

9.【答案】B
 

【解析】解：不相交的两条直线叫平行线，必须是在同一平面内，故错误；
如果两条平行直线被第三条直线所截，那么同位角相等，如果两条不平行直线被第三条直线所截，那么同位角不相等，故错误；
如果两条直线都和第三条直线平行，那么这两条直线平行，正确；
平面内，过一点有且只有一条直线与已知直线垂直，正确；
过直线外一点有且只有一条直线与已知直线平行，故错误，
故选：B．
根据垂线的性质、平行线的性质、平行公理以及其推论分析得出答案．
本题考查了垂线的性质、平行线的性质、平行公理以及其推论，熟记性质和公理是解题关键．
 

10.【答案】C
 

【解析】

【分析】
本题考查的是平行线性质和平角定义的有关知识，利用平行线性质和平角定义解题即可．
【解答】
解：如图：

，，
，
，
，
故选C．  

11.【答案】B
 

【解析】解：直线，
，
，
故选B．
直接根据平行线的性质即可得出结论．
本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．
 

12.【答案】B
 

【解析】

【分析】
本题主要考查的是平行线的性质，折叠的性质的有关知识，由平行线的性质知，进而得到图b中，依据图c中的进行计算．
【解答】
解：，
，
在图b中，
在图c中．
故选B．  

13.【答案】
 

【解析】解：如图．

直线，
，
，
，
，
．
故答案为
由直线，推出，又，由此可得结论．
本题考查平行线的性质，解题的关键是熟练掌握基本知识，属于中考常考题型．
 

14.【答案】
 

【解析】解：，，
，
平分，
，
故结论正确；
，，
，
由，，
，
，
，
，
故结论正确；
，
，
，
，
，
故结论错误．
故答案为：．
根据平行线的性质和，由两直线平行，同旁内角互补，可计算出的度数，再根据角平分线的性质，可计算出的度数．根据，由的度数计算出的度数，根据两直线平行，内错角相等的性质，得到的度数，可计算出的度数，可得出结论．根据平行线的性质，可得到，可计算出的度数，可得出结论．
本题主要考查了平行线的性质角平分线性质的应用，合理应用平行线的性质是解决本题关键．
 

15.【答案】，，，
 

【解析】

【分析】本题考查的是平行线的判定与性质，根据题意画出图形，利用平行线的性质及直角三角板的性质求解是解答此题的关键
根据题意画出图形，再由平行线的判定定理即可得出结论．
【解答】
解：如图，
当时，；
当时，；
当时，，；
当时，，．
故答案为：，，，．
．  

16.【答案】150；135
 

【解析】解：如图b，延长AE到H，由于纸条是长方形，

，
，
根据翻折不变性得，
，，
又，
，．
在梯形FCDG中，，
根据翻折不变性，在图c中．
故答案为：150；135．
根据长方形纸条的对边平行，利用平行线的性质和翻折不变性求出，继而求出图b中的度数，再减掉即可得图c中的度数．
此题主要考查了平行线的性质和图形的折叠，关键是掌握两直线平行，同旁内角互补，折叠前后角的度数不变．
 

17.【答案】
 

【解析】解：过点P作，如图，
，，
，，
，
，
．
故答案为：．
过点P作，如图由平行线的性质，，可得，，由已知，可得由平行线的性质，两直线平行，内错角相等即可得出答案．
本题主要考查了平行线的性质，熟练应用平行线的性质进行求解是解决本题的关键．
 

18.【答案】4
 

【解析】

【分析】

本题主要考查了等腰三角形的性质以及平行线的性质，利用边角关系并结合等量代换来推导证明是本题的特点．根据已知条件，BF、CF分别平分ABC、ACB的外角，且DE BC，可得DBFDFB，ECFEFC，根据等角对等边得出DFBD，CEEF，根据BDCEDE即可求得．

【解答】

解：BF、CF分别平分ABC、ACB的外角，

DBFCBF，FCEFCG，

DE BC，

DFBCBF，EFCFCG，

DBFDFB，FCEEFC，

BDFD，EFCE，

EFDFDEBDDE，

CE．

故答案为4．

19.【答案】证明：，，
，
；
．
理由：，
．
，
，
，
．
 

【解析】本题考查的是平行线的判定与性质，熟知平行线的判定定理是解答此题的关键．
根据对顶角相等得出的度数，再由平行线的判定定理即可得出结论；
先根据得出，再由得出，据此可得出结论．
 

20.【答案】证明：，，
垂直的定义．
同位角相等，两直线平行，
，两直线平行，内错角相等．
，
．
，同位角相等，两直线平行．
两直线平行，同位角相等．
，
．
，即．
 

【解析】依据，，即可得出，进而得到，再根据等量代换即可得到，进而判定，依据，可得．
本题主要考查了平行线的性质与判定，平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．
 

21.【答案】解：，
．
，
．
 

【解析】根据平行线的性质知，结合图形求得的度数．
本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．
 

22.【答案】解：，
，，
为的平分线，
，
，
，
．
 

【解析】根据邻补角的定义和角平分线的定义可求，根据对顶角的定义可求，根据角的和差关系可求，再根据平行线的性质即可求解．
考查了平行线的性质，关键是熟悉两直线平行，内错角相等的知识点．
 

23.【答案】DE  BC  同位角相等，两直线平行  两直线平行，同旁内角互补  EF  AB  同旁内角互补，两直线平行  两直线平行，内错角相等
 

【解析】解：已知，
同位角相等，两直线平行，
两直线平行，同旁内角互补，
已知，
等量代换，
同旁内角互补，两直线平行，
两直线平行，内错角相等．
故答案为：DE；BC；同位角相等，两直线平行；两直线平行，同旁内角互补；EF；AB；同旁内角互补，两直线平行；两直线平行，内错角相等．
先判断出得出，再等量代换，即可判断出即可．
本题考查的是平行线的判定与性质，熟知平行线的判定定理是解答此题的关键．
 

24.【答案】证明：是等边三角形，
，，
将绕点C旋转得到．
，，
是等边三角形，
，
；
将绕点C旋转得到．
，
的周长，
的周长．
 

【解析】由旋转的性质可得，，可得，可证；
由旋转的性质可得，即可求的周长．
本题考查了旋转的性质，等边三角形的判定和性质，平行线的判定和性质，灵活运用旋转的性质是本题的关键．
 

25.【答案】解：一张长方形纸条ABCD折叠，
，
，
，
，
，
，
，
，
是等腰三角形．
 

【解析】根据折叠的性质得出，利用平行线的性质进行解答即可；
根据角的度数得出，进而证明等腰三角形即可．
本题考查了平行线的性质、翻折变换折叠问题正确观察图形，熟练掌握平行线的性质是解题的关键．