


2021学年第七章 相交线与平行线7.5 平行线的性质多媒体教学课件ppt
展开1.掌握平行线的判定与性质定理,能熟练运用平行线的判定与性质定理解决有关问题.(难点)2.掌握平行于同一条直线的两条直线平行并能加以运用.(重点)
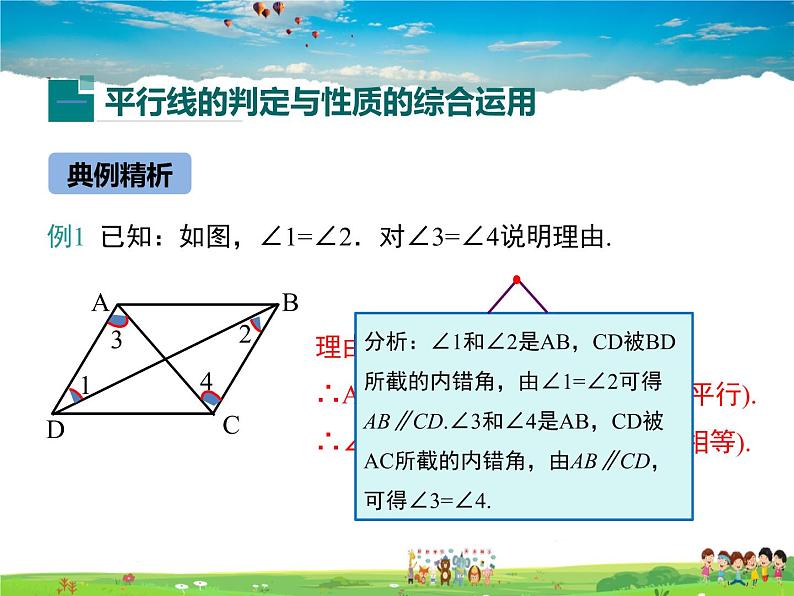
理由:∵∠1=∠2(已知),∴AB∥CD(内错角相等,两直线平行).∴∠3=∠4(两直线平行,内错角相等).
例1 已知:如图,∠1=∠2.对∠3=∠4说明理由.
例2 已知:如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数.
∴∠BAC+AGD=180°
∴∠AGD=180°-BAC=180°-70°=110°.
(两直线平行,同位角相等).
(内错角相等,两直线平行).
(两直线平行,同旁内角互补).
与平行线相关的问题一般都是平行线的判定与性质的综合应用,主要体现在以下两个方面:
1. 由角定角
确定其它角的关系
1.如图所示,下列结论正确的有___________.(把所有正确结论的序号都选上).①若AB∥CD,则∠3=∠4;②若∠1=∠BEG,则EF∥GH;③若∠FGH+∠3=180°,则EF∥GH;④若AB∥CD,∠4=62°,EG平分∠BEF,则1=59°.
2.如图,已知:∠1=∠2,∠D=50°,求∠B的度数.
解:∵∠1=∠2(已知),∠2=∠EHD(对顶角相等),∴∠1=∠EHD(等量代换),∴AB∥CD(同位角相等,两直线平行).∴∠B+∠D=180°(两直线平行,同旁内角互补).∵∠D=50°(已知),∴∠B=180°-50°=130°(等式的性质).
画一画:先画直线l1,再画直线l2,l3分别l1与平行.
想一想:直线l2与l3有怎样的位置关系?
命题3 如图,如果a∥b,a∥c,那么b∥c.
理由: ∵ a∥b ( ), ∴ ∠1=∠2 ( ). ∵ a∥c ( ), ∵ ∠1=∠3 ( ), ∴∠2=∠3 ( ). ∴a∥c ( ).
两直线平行,同位角相等
同位角相等,两直线平行
平行于同一条直线的两直线平行.
∵a // c , a // b (已知), ∴ c // b(平行于同一条直线的两直线平行).
例2 已知:如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC的度数
分析:过点E作EF//AB,
则∠1+∠A=180°.由AB//CD,得EF//CD,则∠C+∠FEC=180°.由∠A=100°, ∠C=110°,可求得∠1和∠FEC的度数,根据角的和差,可求得∠AEC的度数.
解:过点E作EF//AB.∵AB//CD,EF//AB(已知),∴EF//CD(平行于同一直线的两直线平行).∴∠A+∠1=180,∠C+∠FEC=180(两直线平行,同旁内角互补). 又∵∠A=100°,∠C=110°(已知) ∴∠1 =180°-∠A=80 °, ∠FEC=180°-∠C=70 ° (等式的性质) ∴∠AEC=∠1+∠FEC= 80° +70° = 150° .
1.下列推理正确的是( )
A.∵a // d,b // c,∴c // d B.∵a // c,b // d,∴c // dC.∵a // b,a // c,∴b // c D.∵a // b,c // d,∴a // c
2.直线a,b,c,d的位置如图,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于( )A.80° B.65° C.60° D.55°
3.如图,BD⊥AB,BD⊥CD,则∠a的度数是( )A.50° B.40° C.60° D.45°
4.已知AB∥DE,试问∠B,∠E,∠BCE有什么关系.请完成填空:
解:过点C作CF∥AB,则__________ ( ).又∵AB∥DE,AB∥CF,∴____________( ).∴∠E=∠____( ).∴∠B+∠E=∠1+∠2( ), 即∠B+∠E=∠BCE.
平行于同一直线的两条直线平行
两直线平行,内错角相等
5.已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.
解:是.∵AD⊥BC,EG⊥BC(已知),∴∠4=∠5=90°(垂直的定义).∴AD∥EG(同位角相等,两直线平行).∴∠1=∠E(两直线平行,同位角相等), ∠2=∠3(两直线平行,内错角相等).∵∠E=∠3(已知),∴∠1=∠2(等量代换),∴AD是∠BAC的平分线(角平分线的定义).
6.如图,AB,CD,EF,MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,求∠1的度数.
解:∵∠2=∠3=70°(已知),∴AB∥CD(内错角相等,两直线平行),∴∠BGP=∠GPC(两直线平行,内错角相等),∵∠GPC=80°(已知),∴∠BGP=80°(等量代换),∴∠BGM=180°-∠BGP=100°(平角的定义),∵GH平分∠MGB(已知),
7.拓展提升:已知:如图,AB//CD,试解决下列问题:(1)∠1+∠2=___ ___;(2)∠1+∠2+∠3=___ __;(3)∠1+∠2+∠3+∠4=_ __ __;(4)试探究∠1+∠2+∠3+∠4+…+∠n= ;
初中数学冀教版七年级下册7.5 平行线的性质教学演示ppt课件: 这是一份初中数学冀教版七年级下册<a href="/sx/tb_c41352_t3/?tag_id=26" target="_blank">7.5 平行线的性质教学演示ppt课件</a>,共13页。PPT课件主要包含了空白演示等内容,欢迎下载使用。
初中数学冀教版七年级下册7.5 平行线的性质优秀ppt课件: 这是一份初中数学冀教版七年级下册7.5 平行线的性质优秀ppt课件,文件包含河北教育版数学七年级下·75平行线的性质第2课时教学课件pptx、75平行线的性质第2课时教案docx、75平行线的性质第2课时同步练习docx等3份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
数学七年级下册7.5 平行线的性质完美版课件ppt: 这是一份数学七年级下册7.5 平行线的性质完美版课件ppt,文件包含河北教育版数学七年级下·75平行线的性质第1课时教学课件pptx、75平行线的性质第1课时教案docx、75平行线的性质第1课时同步练习docx等3份课件配套教学资源,其中PPT共18页, 欢迎下载使用。