冀教版七年级下册7.5 平行线的性质精品ppt课件

这是一份冀教版七年级下册7.5 平行线的性质精品ppt课件，共47页。PPT课件主要包含了课前导入，新课精讲，学以致用，课堂小结，情景导入，探索新知，典题精讲，易错提醒，小试牛刀等内容，欢迎下载使用。

猜想：交换它们的条件与结论，是否成立？
平行线的内错角相等的性质
性质2 两条平行线被第三条直线所截，内错角相等.
两条平行线被第三条直线截得的内错角会具有怎样的数量关系？
表达方式：如图，因为a∥b(已知)，所以∠1＝∠2(两直线平行，内错角相等)．
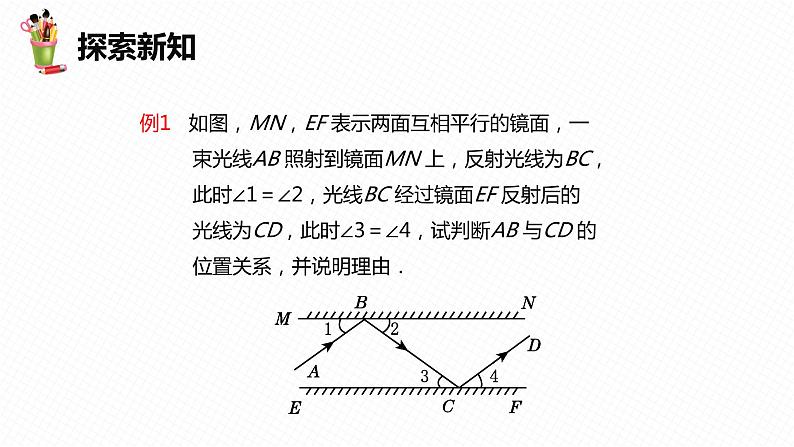
例1 如图，MN，EF 表示两面互相平行的镜面，一 束光线AB 照射到镜面MN 上，反射光线为BC， 此时∠1＝∠2，光线BC 经过镜面EF 反射后的 光线为CD，此时∠3＝∠4，试判断AB 与CD 的 位置关系，并说明理由．
导引：要判断AB 与CD 的位置关系，应从两直线的 位置关系的特殊情况，如平行或垂直方面 思考问题，观察图可知，AB 与CD 没有交点， 所以可猜想AB∥CD，要说明AB∥CD，只 要说明∠ABC＝∠BCD 即可．
解：AB∥CD，理由如下： ∵MN∥EF， ∴∠2＝∠3(两直线平行，内错角相等)． ∵∠1＝∠2，∠2＝∠3，∠3＝∠4， ∴∠1＋∠2＝∠3＋∠4.　　 ∵∠1＋∠ABC＋∠2＝180°， ∠3＋∠BCD＋∠4＝180°， ∴∠ABC＝∠BCD. ∴AB∥CD (内错角相等，两直线平行)．
(1)利用平行线的性质解决实际问题时，其关键是根 据实际问题建立数学模型；(2)判断两直线的位置关系时，一般都从两直线平行 或垂直这两种特殊情况去思考．
如图，一把长方形直尺沿直线断开并错位，点E，D，B，F 在同一条直线上，若∠ADE＝125°，则∠DBC＝(　　)A．55° B．65° C．75° D．125°
已知直线m∥n，将一块含30°角的直角三角尺ABC 按如图方式放置(∠ABC＝30°)，其中A，B 两点分别落在m，n上，若∠1＝20°，则∠2的度数为(　　)A．20° B．30° C．45° D．50°
平行线的同旁内角互补的性质
性质3 两条平行线被第三条直线所截，同旁内角互补.
表达方式：如图，因为a∥b (已知)，所以∠1＋∠2＝180°(两直线平行，同旁内角互补)．
已知：如图，a∥b，c∥d，且∠1＝73°. 求∠2和∠3的度数.
∵a∥b (已知) ，∴∠1＝∠2(两直线平行，内错角相等).∵∠1＝73°(已知)，∴∠2＝73°(等量代换).∵c∥d (已知) ，∴∠2＋∠3＝180°(两直线平行，同旁内角互补)∴∠3＝180°－∠2(等式的性质).∴∠3＝180°－73°＝107° (等量代换).
例3 如图，如果AB∥DF，DE∥BC，且∠1＝65°，那么你能说出∠2，∠3，∠4的度数吗？为什么？导引：由DE∥BC，可得∠1＝∠4，∠1＋∠2＝180°；由DF∥AB，可得∠3＝∠2，从而得∠2，∠3，∠4的度数．
解：∵DE∥BC (已知)， ∴∠4＝∠1＝65°(两直线平行，内错角相等)， ∠2＋∠1＝180°(两直线平行，同旁内角互补)． ∴∠2＝180°－∠1＝180°－65°＝115°. 又∵DF∥AB (已知)， ∴∠3＝∠2(两直线平行，同位角相等)． ∴∠3＝115°(等量代换)．
1.求角的度数的基本思路：根据平行线的判定由角的数量 关系得到直线的位置关系，根据平行线的性质由直线的 位置关系得到角的数量关系，通过上述相互转化，从而 找到所求角与已知角之间的关系．2.两直线平行时，应联想到平行线的三个性质，由两条直 线平行的位置关系得到两个相关角的数量关系，由角的 关系求相应角的度数．
下面写出了命题“如图，如果∠B＝∠C，那么∠A＋∠1＝180°”的说理过程，请你填空：∵ ∠B＝∠C ( )，∴_____∥_____( ).∴∠A＋∠1＝180°( ).
内错角相等，两直线平行
两直线平行，同旁内角互补
如图，若直线a∥b，则图中与∠1互补的角有(　　)A．2个 B．3个 C．4个 D．5个
如图，∠1＝60°，若CD∥BE，则∠B 的度数为(　　)A．70° B．100° C．110° D．120°
如图，直线AB∥CD，AE 平分∠CAB，AE 与CD 相交于点E，∠ACD＝40°，则∠BAE 的度数是(　　)A．40° B．70° C．80° D．140°
平行线的判定和性质的应用
如图，已知∠ABC 与∠ECB 互补，∠1＝∠2，则∠P 与∠Q 一定相等吗？说说你的理由．
如果∠P 和∠Q 相等，那么PB∥CQ，所以要判断∠P 与∠Q 是否相等，只需判断PB 和CQ 是否平行．要说明PB∥CQ，可以通过说明∠PBC＝∠BCQ 来实现，由于∠1＝∠2，只需说明∠ABC＝∠BCD 即可．
一定．理由如下：因为∠ABC 与∠ECB 互补(已知)，所以AB∥ED (同旁内角互补，两直线平行)．所以∠ABC＝∠BCD (两直线平行，内错角相等)．因为∠1＝∠2(已知)，所以∠ABC－∠1＝∠BCD－∠2(等式的性质)，即∠PBC＝∠BCQ.所以PB∥CQ (内错角相等，两直线平行)．所以∠P＝∠Q (两直线平行，内错角相等)．
一个数学问题的构成含有四个要素：题目的条件、解题的依据、解题的方法、题目的结论，如果题目所含的四个要素解题者已经知道或者结论虽未指明，但它是完全确定的，这样的问题就是封闭性的数学问题．
如图，下列结论中不正确的是(　　)A．若AD∥BC，则∠1＝∠B B．若∠1＝∠2，则AD∥BCC．若∠2＝∠C，则AE∥CD D．若AE∥CD，则∠1＋∠3＝180°
如图，在三角形ABC 中，CE⊥AB 于E，DF⊥AB 于F，AC∥ED，CE 是∠ACB 的平分线，则图中与∠FDB 相等的角(不包含∠FDB )的个数为(　　)A．3 B．4 C．5 D．6
已知∠1与∠2是同旁内角．若∠1＝50°，则∠2的度数是(　　)A．50°　 B．130°　 C．50°或130°　 D．不能确定
易错点：利用平行线的性质时易忽视两直线平行这一前提而出错.
如图，已知AB∥CD∥EF，FC 平分∠AFE，∠C＝25°，则∠A 的度数是(　　)A．25° B．35° C．45° D．50°
如图，已知a∥b，直角三角尺的直角顶点在直线b上，若∠1＝60°，则下列结论错误的是(　　)A．∠2＝60° B．∠3＝60°C．∠4＝120° D．∠5＝40°
如图，若∠1＝∠2，DE∥BC，则下列结论：①FG∥DC；②∠AED＝∠ACB；③CD 平分∠ACB；④∠1＋∠B＝90°；⑤∠BFG＝∠BDC，其中正确的是(　　)A．①②③ B．①②⑤C．①③④ D．③④
如图，AB∥CD，点E 是CD上一点，∠AEC＝42°，EF 平分∠AED 交AB 于点F，求∠AFE 的度数．
∵∠AEC＝42°，∠AEC＋∠AED＝180°，∴∠AED＝180°－∠AEC＝138°.∵EF 平分∠AED，∴∠DEF＝ ∠AED＝69°.又∵AB∥CD，∴∠AFE＝∠DEF＝69°.
如图是某次考古发掘出的一个四边形残缺玉片，工作人员从玉片上已经量得∠A＝115°，∠D＝110°，已知在四边形中，AD∥BC，请你帮助工作人员求出另外两个角的度数．
因为AD∥BC (已知)，所以∠A＋∠B＝180°，∠C＋∠D＝180°(两直线平行，同旁内角互补)．所以∠B＝180°－∠A＝180°－115°＝65°，∠C＝180°－∠D＝180°－110°＝70°.
如图，已知AB∥CD，EF⊥AB 于点O，∠FGC＝125°，求∠EFG 的度数．下面提供三种思路： (1)过点F 作FH∥AB； (2)延长EF 交CD 于M； (3)延长GF 交AB 于K.请你利用三个思路中的两个思路，将图形补充完整，求∠EFG 的度数．
答案不唯一，如选用思路(1)和(2)．(一)利用思路(1)，过点F 作FH∥AB，如图①.∵EF⊥AB，∴∠BOF＝90°.∵FH∥AB，∴∠HFO＝∠BOF＝90°.∵AB∥CD，∴FH∥CD.∴∠FGC＋∠GFH＝180°.∵∠FGC＝125°，∴∠GFH＝55°.∴∠EFG＝∠GFH＋∠HFO＝55°＋90°＝145°；
(二)利用思路(2)，延长EF 交CD 于M，如图②.∵EF⊥AB，∴∠BOF＝90°.∵CD∥AB，∴∠CMF＝∠BOF＝90°.∵∠FGC＝125°，∴∠1＝55°.∵∠1＋∠2＋∠GMF＝180°，∴∠2＝35°.∵∠GFO＋∠2＝180°，∴∠GFO＝145°，即∠EFG＝145°.
直线AB∥CD，点P 是直线AB，CD 外的任意一点，连接PA，PC. (1)探究猜想：①如图①，若∠A＝30°，∠C＝40°，则∠APC＝________°；
②如图①，若∠A＝40°，∠C＝60°，则∠APC＝________°；③猜想图①中∠A，∠C，∠APC 三者之间有怎样的等量关系？并说明理由．
∠APC＝∠A＋∠C.理由如下：过P 点向左侧作PE∥AB，∴∠APE＝∠A，∵AB∥CD，∴PE∥CD，∴∠CPE＝∠C.又∵∠APC＝∠APE＋∠CPE，∴∠APC＝∠A＋∠C.
(2)拓展：①如图②，若∠A＝20°，∠C＝50°，则∠APC＝________°；②猜想图③中∠A，∠C，∠APC 三者之间的关系为 ．
平行线的性质：两直线平行，内错角相等．两直线平行，同旁内角互补．